データの自動分類:クラスタ分析入門

AIを知りたい
先生、クラスタ分析って、結局何をするものなんですか?

AIエンジニア
簡単に言うと、似たもの同士をグループ分けすることだよ。例えば、色々な果物があったら、大きさや色、味などでグループ分けできるよね。クラスタ分析も同じように、データの特徴を見て、似たデータ끼리まとめていくんだ。

AIを知りたい
なるほど。でも、果物の例だと、人間が見て判断できますけど、コンピュータはどうやって判断するんですか?

AIエンジニア
良い質問だね。コンピュータは、k-means法といったやり方を使うんだ。これは、あらかじめいくつのグループに分けるかを決めておいて、データの特徴を数値でとらえ、似た数値のデータ끼리まとめていく方法だよ。例えば、リンゴとみかん、ぶどう、バナナがあったら、大きさ、色、甘さなどを数値で表して、4つのグループに分ける、といった具合だね。
クラスタ分析とは。
人工知能で使われる言葉の一つに『集団分け分析』というものがあります。これは、人間が教えなくてもコンピューターが自分で学習するやり方の一つで、たくさんのデータをいくつかの集団(かたまり)に分ける分析のことです。この分析では、データの集団の数をあらかじめ決めて、それぞれの集団の中心点を決める『中心点方式』という方法がよく使われます。
集団分けの仕組み

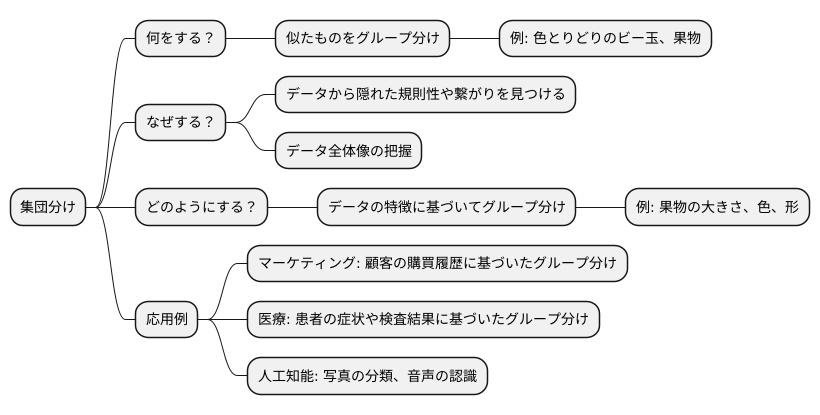
たくさんの物が混ざり合っている様子を思い浮かべてみてください。例えば、色とりどりのビー玉の山や、様々な種類の果物が盛られた籠などです。これらの物の中から、似たものを集めてグループ分けしたい場合、どのようにすれば良いでしょうか。一つ一つ手に取って見比べていくのは大変な作業です。そこで役立つのが、集団分けの仕組みです。
集団分けは、様々なデータの中から、似ているもの同士を自動的にグループにまとめる方法です。この方法を使うと、データの山の中から隠れた規則性や繋がりを見つけることができます。まるで、霧の中に隠されていた景色が、霧が晴れると鮮やかに見えるようになるかのようです。大量のデータが整理され、データの背後にある全体像が明らかになるのです。
具体的な例を挙げると、果物の集団分けを考えてみましょう。リンゴ、バナナ、ミカン、ブドウ、イチゴなど、様々な果物が混ざっています。これらの果物を大きさ、色、形といった特徴に基づいてグループ分けすると、どうなるでしょうか。赤い色の小さなものはイチゴのグループに、黄色くて曲がったものはバナナのグループに、丸くて皮が剥けるものはミカンやオレンジのグループに、といった具合に、似た特徴を持つ果物同士が自然とグループ分けされます。
この集団分けの仕組みは、様々な場面で活用されています。例えば、お店の顧客を購買履歴に基づいてグループ分けすることで、それぞれのグループに合った商品を宣伝することができます。また、病院では、患者の症状や検査結果に基づいてグループ分けすることで、より適切な治療方針を立てることができます。さらに、写真の分類や音声の認識など、人工知能の分野でも、この仕組みは重要な役割を担っています。このように、集団分けは、複雑なデータの中から意味のある情報を取り出すための、強力な道具と言えるでしょう。
代表的手法:k-means法

集団分けのやり方にはいろいろありますが、中でもよく使われるのが「k平均法」です。このやり方では、まず何個の集団に分けたいかを決めます。この集団の数を「k」と呼びます。例えば、3つの集団に分けたい場合はk=3となります。
次に、集められたデータの中からでたらめにk個の点を選びます。これらの点は、それぞれの集団の真ん中の点(中心点)の最初の位置となります。k=3の場合は、3つの点が選ばれます。
そして、集められたデータの一つ一つを見て、どの真ん中の点に一番近いかを調べます。一番近い真ん中の点の集団に、そのデータを仲間入りさせます。こうして、全てのデータがどこかの集団に所属することになります。
次に、各集団に属するデータの平均値を計算します。この平均値が、その集団の新しい真ん中の点となります。
この「データを真ん中の点に近い集団に割り当てる」作業と「各集団の新しい真ん中の点を計算する」作業を何度も繰り返します。これを繰り返すことで、真ん中の点が動かなくなったり、あらかじめ決めた回数繰り返したりするまで続けます。
k平均法は、やり方が分かりやすい割に、うまく集団分けができるので、色々な場面で使われています。しかし、最初に真ん中の点をでたらめに決めるので、計算するたびに結果が少し変わることがあります。また、集団の数を最初に決める必要があるため、適切な集団の数が分からない場合は試行錯誤が必要になることもあります。
適切な集団数の決め方

集団を適切な数に分割する手法の一つとして、k平均法というものがあります。この手法では、集団をいくつかの小さな集団(グループ)に分割するために、あらかじめいくつのグループに分けるか(kの値)を決めておく必要があります。しかし、このkの値を適切に決めるのは容易ではありません。一体どのように決めれば良いのでしょうか?
一つの有効な方法として、ひじ法と呼ばれる手法があります。この手法では、まずグループの数(kの値)を小さい値から少しずつ大きくしながら、それぞれのkの値に対して、各グループ内のデータの散らばり具合を計算します。kの値が小さいうちは、kの値を1つ増やすごとに、散らばり具合は大きく減少します。しかし、kの値がある程度大きくなると、kの値を1つ増やしても散らばり具合の減少幅は小さくなります。グラフを描いてこの様子を可視化すると、散らばり具合の減少幅が小さくなるあたりで、グラフの線が折れ曲がるため、この手法をひじ法と呼びます。そして、この折れ曲がり地点におけるkの値を、適切なグループ数と判断します。
ひじ法は、グラフを描いて視覚的に判断するため、比較的分かりやすい方法です。しかし、折れ曲がり地点がはっきりとしない場合もあり、判断に迷うケースも少なくありません。そのような場合には、ひじ法だけで判断するのではなく、他の指標や分析結果も参考にしながら、kの値を慎重に決定する必要があります。例えば、実際に分割されたグループの中身を見て、それぞれのグループに意味のある特徴があるかを確認することも重要です。
kの値を決める際には、分析の目的やデータの特性を考慮することも大切です。例えば、顧客をグループ分けしてそれぞれに合った販売戦略を立てる場合、あまりにも細かすぎるグループ分けは、かえって非効率になる可能性があります。また、データの量が少ない場合、kの値を大きくしすぎると、各グループに属するデータ数が少なくなってしまい、分析結果の信頼性が低下する可能性があります。そのため、kの値を決める際には、様々な要素を総合的に判断することが重要です。
活用の場

物の集まりを似た者同士でグループ分けする手法、それがクラスタ分析です。この手法は、様々な分野で活用され、データに基づいた的確な判断を助けてくれます。例えば、販売促進の分野では、顧客を過去の買い物や持ち合わせている特徴でグループ分けすることで、それぞれのグループに合わせた商品やサービスの提供を可能にします。過去の買い物データから「よくお菓子を買うグループ」「お酒をよく買うグループ」などに顧客を分類し、それぞれに合わせたクーポンを発行するといった具合です。医療の分野でも、患者の症状や検査結果からグループ分けすることで、病気の診断や治療方針の決定に役立てることができます。似た症状を持つ患者をグループ分けすることで、より効果的な治療法を見つけ出す手がかりになります。
また、画像認識の分野では、画像の持つ特徴に基づいて小さな点の集まりである画素をグループ分けすることで、写っている物の識別や画像データの圧縮を可能にします。例えば、空や雲、建物といった要素ごとに画素をグループ分けすることで、画像に何が写っているかをコンピュータが理解できるようになり、自動運転技術などへの応用も期待されます。さらに、クラスタ分析は、不正利用の検知にも役立ちます。クレジットカードの利用履歴を分析し、普段とは異なる利用パターンを検出することで、不正利用の早期発見に繋がります。
このように、クラスタ分析は大量のデータから有用な情報を見つけ出し、物事を決める際に役立つ情報を提供する強力な手法です。今後、データ活用の重要性が増すにつれて、クラスタ分析の活躍の場はますます広がっていくでしょう。ビジネスや医療、科学技術など、様々な分野での応用が期待され、データに基づいたより良い社会の実現に貢献していくと考えられます。
| 分野 | 活用例 |
|---|---|
| 販売促進 | 顧客を購買履歴や属性でグループ分けし、それぞれに最適な商品・サービスを提供(例:お菓子をよく買うグループ、お酒をよく買うグループ)。 |
| 医療 | 患者の症状や検査結果でグループ分けし、病気の診断や治療方針決定を支援。 |
| 画像認識 | 画像の画素を特徴に基づきグループ分けし、物体識別やデータ圧縮を実現(例:空、雲、建物など)。 |
| 不正利用検知 | クレジットカードの利用履歴を分析し、普段と異なる利用パターンを検出。 |
分析時の注意点

物事をいくつかの集まりに分ける作業、いわゆる集団分け分析を行う際には、いくつか気を付けるべき点があります。まず、分析前の準備が大切です。集まりに分ける対象となるデータに、情報が欠けている部分や、明らかに他のデータと大きく異なる値が含まれていると、分けられた結果に影響が出てしまうことがあります。そのため、分析を始める前に、データの不足部分を補ったり、大きく外れた値を取り除いたり、適切な形に変換するなどの作業が必要です。
たとえば、よく使われる「K平均法」という集団分けの方法では、集団の中心となる点の最初の選び方によって、結果が変わってしまうことがあります。同じデータを分析する場合でも、中心点の選び方が異なれば、分けられた集団も変わってくるのです。そのため、分析を何回か繰り返して、結果が大きく変わらないことを確かめることが重要です。
また、K平均法は、数値データ、つまり数量で表されるデータに適した方法です。物の種類や名前など、数値ではないデータには適していません。たとえば、果物の種類や色などをK平均法で分析するのは難しいでしょう。種類や名前といった数値ではないデータを分析する場合は、K平均法以外の集団分けの方法を考える必要があります。
これらの点に注意することで、より正確で信頼できる分析結果を得ることができます。適切な分析前の準備、何回かの分析の繰り返し、データの種類に合った方法の選択など、分析の精度を高めるための工夫を凝らすことが大切です。そうすることで、本当に意味のある集団分けの結果を得ることができ、より良い判断へと繋げることができるでしょう。
| 注意点 | 詳細 | 例 |
|---|---|---|
| 分析前のデータ準備 | 欠損値、異常値への対処、適切な形への変換 | – |
| 初期値依存性への対処 | 初期値(K平均法では中心点)の選び方によって結果が変わる可能性があるため、複数回実行し安定性を確認 | K平均法 |
| データの種類に適した方法の選択 | 数値データに適した方法(K平均法など)と、非数値データに適した方法を使い分ける | 数値データ:K平均法、非数値データ:K平均法以外 |
まとめ

まとめとして、今回の記事ではデータの集団分けに役立つクラスタ分析について解説しました。クラスタ分析は、あらかじめ正解が与えられていないデータから、似たもの同士をまとめて集団を作る手法で、教師なし学習と呼ばれるデータ分析の方法の一つです。この手法を使うことで、データの中に隠れている構造や規則性を見つけることができます。
クラスタ分析の中でも、よく使われる手法の一つがk-平均法です。k-平均法は、あらかじめ幾つの集団に分けるかを決めておき、それぞれの集団の中心点を計算しながら、データがどの集団に属するかを調整していく方法です。比較的簡単な計算で結果を得ることができるため、広く利用されています。
しかし、k-平均法を使う際にはいくつか注意すべき点があります。例えば、集団の数を適切に決めることが重要です。少なすぎるとデータの特徴を捉えきれず、多すぎると細かすぎる分類になってしまいます。また、データの性質によっては、事前にデータの尺度を揃えたり、外れ値と呼ばれる極端に大きな値や小さな値を持つデータを処理したりする必要があります。これらの前処理を適切に行うことで、より正確な分析結果を得ることができます。
クラスタ分析は、様々な分野で活用されています。例えば、販売促進の分野では顧客をグループ分けして、それぞれに合った販売戦略を立てるのに役立ちます。医療の分野では患者の症状をグループ分けして、病気の診断や治療方針の決定に役立てることができます。また、画像認識の分野では、画像の特徴を捉えて画像を分類するのに役立ちます。このように、クラスタ分析はデータから有益な情報を取り出すための強力な手法と言えるでしょう。
データ活用の重要性が高まる現代社会において、クラスタ分析を理解し、使いこなせることは大きな強みとなります。この記事をきっかけに、クラスタ分析について学び、実践することで、データ分析のスキル向上に繋がるでしょう。ぜひ、クラスタ分析を学び、データ分析の新たな可能性を探ってみてください。
| 手法 | 説明 | メリット | デメリット/注意点 | 活用例 |
|---|---|---|---|---|
| クラスタ分析 | 教師なし学習の一つ。正解データなしで似たもの同士をまとめて集団を作る。 | データの隠れた構造や規則性発見 | – | – |
| k-平均法 | クラスタ分析の一種。あらかじめ集団数を決めて、中心点を計算しながらデータの所属先を調整。 | 比較的簡単な計算 |
|
|
