状態価値関数:強化学習の基礎

AIを知りたい
状態価値関数って、何ですか?難しそうでよくわからないです。

AIエンジニア
そうですね、少し難しいですね。簡単に言うと、ある場所にどれだけの価値があるかを示す関数のことです。例えば、宝探しのゲームで考えてみましょう。宝がある場所に近ければ近いほど、その場所の価値は高くなりますよね。

AIを知りたい
なるほど。宝に近いほど価値が高い、というのは分かります。でも、AIとどう関係があるのですか?

AIエンジニア
AI、特に強化学習では、AI自身が試行錯誤しながら目的を達成する方法を学習します。この時、状態価値関数は、AIが今いる状況が良いか悪いかを判断するのに役立ちます。宝探しの例で言うと、AIは状態価値関数が高い場所を選んで進むことで、最終的に宝を見つけられる可能性が高くなるのです。
状態価値関数とは。
人工知能の分野で出てくる「状態価値関数」について説明します。強化学習という技術では、最終的に得られる報酬の合計を最大にすることを目指しています。そのため、状態価値関数と行動価値関数というものが重要になります。状態価値関数は、目標に近いほど値が大きくなるので、人工知能はこの値を参考に次の行動を決めます。
はじめに

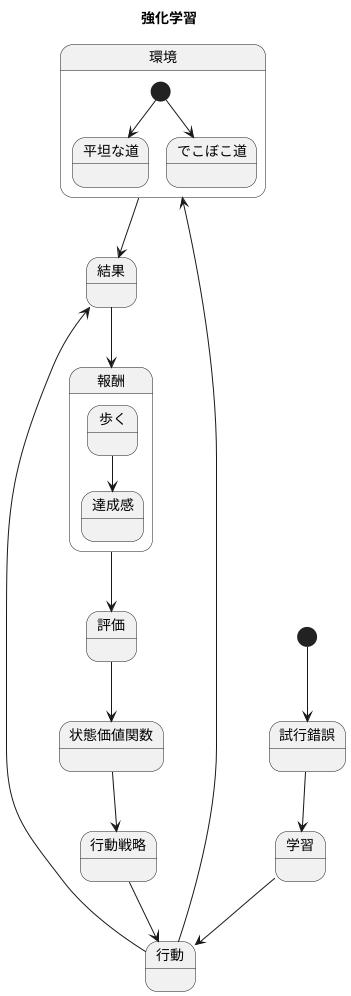
機械学習の中で、試行錯誤を通して学習していく方法を強化学習と呼びます。人間の学習と似ていて、赤ちゃんの歩き方を学ぶ過程を想像してみてください。最初は転んだり、うまく歩けなかったりするかもしれません。しかし、何度も繰り返すうちに、どのように足を動かし、バランスを取れば良いのかを徐々に理解し、最終的には上手に歩けるようになります。強化学習もこれと同じように、機械が様々な行動を試してみて、その結果に応じて学習を進めていきます。
強化学習の目的は、環境との関わりの中で得られる報酬の合計値を最大にすることです。先ほどの赤ちゃんの例で言えば、歩くことができた時の達成感や喜びが報酬にあたります。機械も同様に、目的を達成した時に報酬が与えられ、より多くの報酬を得られるように行動を調整していきます。この報酬を最大化するために、機械は最適な行動戦略を学ぶ必要があります。どの場面でどのような行動をとれば、最も多くの報酬を得られるかを試行錯誤しながら学習していくのです。
この学習過程において、状態価値関数というものが重要な役割を担います。状態価値関数は、機械が現在置かれている状況が良い状態なのか悪い状態なのかを評価する関数です。例えば、赤ちゃんが歩いている途中で、平坦な道にいるのか、それともでこぼこした道にいるのかによって、転ぶ危険性は変わってきます。平坦な道は安全で良い状態、でこぼこした道は危険で悪い状態と言えるでしょう。状態価値関数は、このように機械が置かれている状況の良し悪しを数値化し、将来どのくらいの報酬が得られるかを予測します。そして、この予測に基づいて、機械は次にどのような行動をとるべきかを決めるのです。つまり状態価値関数は、機械が最適な行動を選択するための羅針盤のような役割を果たしていると言えるでしょう。
状態価値関数の定義

状態価値関数は、強化学習において重要な概念であり、エージェントがある状態に置かれたときに、そこから将来にわたってどれだけの報酬を得られるかを予測する関数です。具体的には、ある状態から行動を開始し、決められた手順に従って行動を続けた場合に、最終的に得られると予想される報酬の合計を表します。この合計には、将来得られる報酬ほど割引が適用されます。つまり、すぐに得られる報酬は価値が高く、遠い未来に得られる報酬は価値が低いとみなされます。
この関数を理解する上で重要なのは、「手順」と「状態」です。手順とは、エージェントが各状態でどのような行動を選ぶかを定めた規則です。例えば、迷路を解く場面では、「可能な限り右に進む」といった規則が手順となります。状態とは、エージェントが置かれている状況です。迷路の例では、エージェントがいるマス目が状態となります。状態価値関数は、この状態と手順を入力として受け取り、期待される報酬の合計を出力します。
最適な状態価値関数というものも存在します。これは、あらゆる手順の中で、最大の期待報酬の合計を与える状態価値関数です。言い換えれば、どんな手順よりも優れた結果を生み出す手順に従った場合の、状態の価値を示すものです。この最適な状態価値関数を求めることが、強化学習の主要な目標の一つです。最適な状態価値関数を見つけることで、エージェントはどんな状況でも最良の行動を選択できるようになり、最大の報酬を得ることが可能になります。
| 概念 | 説明 |
|---|---|
| 状態価値関数 | エージェントがある状態に置かれたとき、そこから将来にわたって得られる報酬の合計を予測する関数。将来の報酬には割引が適用される。 |
| 手順 | エージェントが各状態でどのような行動を選ぶかを定めた規則 (例: 迷路で「可能な限り右に進む」) |
| 状態 | エージェントが置かれている状況 (例: 迷路でエージェントがいるマス目) |
| 入力 | 状態と手順 |
| 出力 | 期待される報酬の合計 |
| 最適な状態価値関数 | あらゆる手順の中で最大の期待報酬の合計を与える状態価値関数。 |
状態価値関数の役割

状態価値関数は、強化学習において将来の報酬を予測するために重要な役割を担います。 これは、ある状態にエージェントがいるとき、そこからどのくらいの累積報酬を得られるかを予測する関数です。言い換えると、エージェントが特定の状態に置かれたときに、そこから将来にわたって得られる報酬の期待値を表すものです。
状態の価値が高い場合、その状態から開始することで、将来多くの報酬が得られると期待できます。 例えば、迷路を解く課題を考えると、ゴールに近い状態は価値が高くなります。なぜなら、ゴールに到達すれば高い報酬が得られるからです。逆に、スタート地点から遠い袋小路のような状態は価値が低くなります。このような状態に陥ると、ゴールに到達するまでに時間がかかり、報酬を得るまでに多くのステップが必要になるからです。
エージェントはこの状態価値関数を用いて行動を決定します。 各状態での価値を把握することで、より価値の高い状態へと遷移するように行動を選択できます。迷路の例では、エージェントは価値の高い状態、つまりゴールに近い状態を目指して移動することで、最終的にゴールに到達し報酬を得ることができます。
さらに、状態価値関数は、方策の評価にも役立ちます。 方策とは、エージェントが各状態でどのような行動をとるかを定めたものです。ある方策に従って行動した場合の各状態の価値を計算することで、その方策の良し悪しを評価できます。価値の高い状態へと遷移するような方策は、良い方策とみなされます。状態価値関数が示す価値が高ければ高いほど、その方策はより多くの報酬を得られると期待できるからです。このように状態価値関数は、強化学習においてエージェントが最適な行動を学習する上で、なくてはならない役割を担っています。
状態価値関数の計算方法

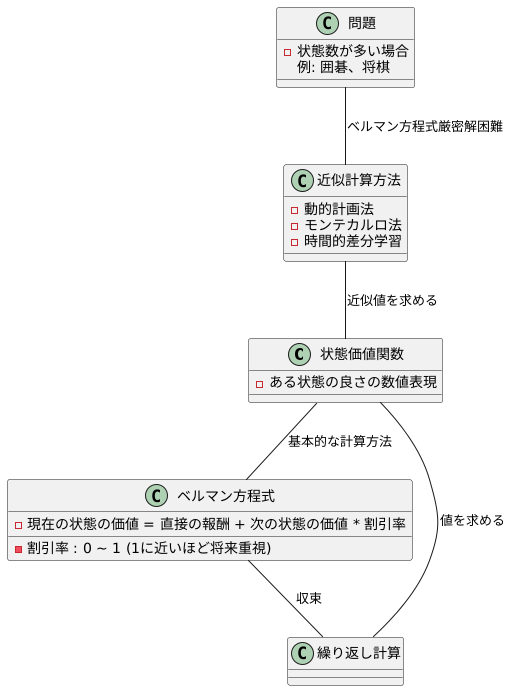
状態価値関数とは、ある状態にいることがどれくらい良いかを数値で表したものです。この値を計算する方法はいくつかありますが、基本となるのはベルマン方程式と呼ばれるものです。
ベルマン方程式は、現在の状態の価値と将来の価値との関係を式で表したものです。具体的には、ある状態の価値は、その状態で得られる直接の報酬と、次に移る可能性のある状態の価値の合計で決まります。ただし、将来の価値は、時間経過とともにその重要性が薄れていくことを考慮する必要があります。そこで、割引率という値を導入し、将来の価値にこの割引率をかけ合わせます。割引率は0から1の間の値で、1に近いほど将来の価値を重視することを意味します。
このベルマン方程式を繰り返し計算することで、状態価値関数の値を求めることができます。計算を繰り返すたびに、将来の状態の価値が現在の状態の価値に反映され、最終的にはすべての状態の価値が収束します。
しかし、現実の問題では、状態の数が非常に多くなる場合がしばしばあります。例えば、囲碁や将棋のようなゲームでは、考えられる盤面の状態の数は天文学的になります。このような場合、ベルマン方程式を厳密に解くことは計算時間の観点から現実的ではありません。そこで、近似的な計算方法が用いられます。代表的な近似計算方法としては、動的計画法、モンテカルロ法、時間的差分学習などがあります。これらの手法は、状態価値関数を完全に正確に計算することはできませんが、実用上十分な精度で近似値を求めることができます。
状態価値関数の応用

状態価値関数は、様々な分野で活用される強力な道具です。ある状況における価値を数値化することで、将来的な見通しを予測し、最適な行動を選択するための指針となります。具体的には、ゲーム、機械の制御、資源の管理など、幅広い分野で応用されています。
ゲームにおいては、状態価値関数はプレイヤーの戦略学習に役立ちます。例えば、囲碁や将棋のような複雑なゲームでは、盤面の状況すべてを評価することは困難です。しかし、状態価値関数を使うことで、現在の盤面の状態がどの程度有利かを数値化できます。この数値を基に、プレイヤーはより良い手を考えることができます。コンピュータは状態価値関数を学習することで、人間の熟練者に匹敵、あるいは凌駕する強さを身につけることができるのです。
機械の制御、特にロボットの制御においても、状態価値関数は重要な役割を果たします。ロボットがある作業を行う際、目標を達成するために最適な行動の順番を決定する必要があります。状態価値関数を用いることで、ロボットは現在の状態から目標達成までの見通しを評価し、最適な行動を選択できます。例えば、工場で部品を組み立てるロボットは、部品の位置や向きといった状況を把握し、最も効率的な組み立て手順を学ぶことができます。
資源の管理においても、状態価値関数は有効な手段となります。限られた資源を効率的に利用するためには、資源の配分を最適化する必要があります。状態価値関数を用いることで、資源の現在の状態と将来的な需要を予測し、最適な配分計画を立てることができます。例えば、電力網の管理では、電力需要の変動を予測し、安定した電力供給を維持するために発電所の出力を調整することができます。このように、状態価値関数は様々な場面で我々の生活を支える重要な技術となっています。
| 分野 | 状態価値関数の役割 | 例 |
|---|---|---|
| ゲーム | プレイヤーの戦略学習、盤面の状況評価 | 囲碁、将棋 コンピュータが盤面の状態を評価し、最適な手を選択 |
| 機械の制御 | 目標達成のための最適な行動の順番決定 | ロボットの制御 工場で部品を組み立てるロボットが効率的な手順を学習 |
| 資源の管理 | 資源の配分最適化、将来的な需要予測 | 電力網の管理 電力需要の変動予測に基づき発電所の出力を調整 |
まとめ

強化学習という学び方において、状態価値関数という考え方はとても大切なものです。これは、ある状況での価値、つまり将来どれだけの良い結果が得られるかを数値で表したものです。例えるなら、囲碁で今の盤面が良いか悪いかを判断するようなものです。エージェント、つまり学習する主体は、この状態価値関数を使って、どの行動が最も良いかを判断します。まるで囲碁でどの手が最も有利かを考えるように、将来の報酬を最大化するために、最も価値の高い状態へと導く行動を選びます。
状態価値関数は、まるで未来を予測する水晶玉のような役割を果たします。今の行動が将来どのような結果をもたらすかを予測し、より良い結果につながる行動を選択するための指針となります。例えば、ロボットに物を掴むことを学習させるとき、状態価値関数はロボットの腕の位置や掴む物の形状などから、成功する確率を予測します。そして、最も成功確率の高い動きをロボットに選ばせるのです。
状態価値関数を計算する方法は様々ありますが、基本的には将来得られる報酬の合計を現在時点の価値に換算することで計算します。この計算は複雑な場合が多く、より効率的な計算方法の開発は、強化学習の分野における重要な課題の一つです。より高度な計算方法が開発されれば、複雑な問題にも強化学習を適用できるようになり、様々な分野での応用が期待できます。例えば、自動運転技術や、医療診断、金融取引など、様々な分野で活用できる可能性を秘めています。
状態価値関数の研究は、強化学習の発展を大きく左右する重要な要素です。より複雑な状況や、変化の激しい環境にも対応できるような、新しい計算方法や理論の開発が期待されています。今後、状態価値関数の研究がさらに進展することで、強化学習はより高度な問題解決に役立ち、私たちの生活をより豊かにする技術となるでしょう。
