白色化:データの前処理

AIを知りたい
先生、「白色化」って標準化と何が違うんですか?どちらもデータを整える処理みたいですが…

AIエンジニア
いい質問だね。どちらもデータを扱いやすくする処理だけど、標準化はそれぞれのデータのばらつきを整えるのに対し、白色化はデータ同士の「関係性」をなくすところが違うんだ。

AIを知りたい
データ同士の「関係性」ですか?

AIエンジニア
そう。例えば、身長と体重は関係性があることが多いよね? 白色化はこういった関係性をなくし、より独立したデータに変換する処理なんだよ。そして、白色化した後に標準化を行うことで、データのばらつきも整えるんだ。
白色化とは。
人工知能の分野でよく使われる「白色化」という用語について説明します。白色化とは、データのばらつきを整える「標準化」をさらに進めた手法です。標準化では、それぞれのデータの値が平均0、ばらつき1になるように調整します。白色化では、それに加えて、データのそれぞれの要素間の関係性をなくします。つまり、データの要素同士が互いに影響を与えないようにすることで、より精密な分析を可能にします。
白色化とは

{白色化とは、機械学習で扱うデータの前処理に使われる大切な技術です。データを整えることで、学習の効率を高め、結果の精度を向上させる効果があります。具体的には、データの特徴どうしの関係性をなくし、データの分布をある形に変換します。
白色化と似た処理に標準化がありますが、両者は異なります。標準化は、データの平均をゼロ、ばらつき具合を表す分散を1にします。これは、異なる尺度を持つデータを同じ土俵で比較できるように調整するための処理です。一方、白色化は、データの特徴どうしの繋がり具合を示す共分散行列を単位行列に変換します。つまり、特徴どうしの相関を完全に消し、それぞれの特徴が互いに独立するようにするのです。
例えるなら、複数の楽器がバラバラに音を奏でている状態を想像してみてください。それぞれの楽器の音は他の楽器に影響されず、独立しています。白色化は、データの特徴をこのようなバラバラの楽器の音のように変換する処理と言えるでしょう。
白色化を行うことで、データは平均がゼロ、分散が1の正規分布に従うようになります。正規分布とは、平均値を中心に左右対称に広がる釣鐘型の分布のことです。多くの機械学習モデルは、データが正規分布に従っていると仮定して設計されているため、白色化によってデータの分布を正規分布に近づけることは、モデルの性能向上に繋がります。
このように、白色化は標準化の機能を含みつつ、データの特徴間の関係性も調整する、より高度なデータの前処理手法と言えるでしょう。
| 項目 | 説明 |
|---|---|
| 白色化 | データの特徴どうしの関係性をなくし、データの分布を正規分布に変換する前処理技術。特徴間の相関をなくし、それぞれの特徴が独立するように変換する。 |
| 標準化 | データの平均をゼロ、分散を1にする処理。異なる尺度を持つデータを同じ土俵で比較できるように調整する。 |
| 白色化と標準化の違い | 標準化は平均と分散を調整するのに対し、白色化は共分散行列を単位行列に変換することで特徴間の相関を完全に消す。白色化は標準化の機能を含み、かつ特徴間の関係性も調整する。 |
| 白色化の効果 | データは平均がゼロ、分散が1の正規分布に従うようになる。多くの機械学習モデルはデータが正規分布に従っていると仮定しているため、モデルの性能向上に繋がる。 |
| 例え | 複数の楽器がバラバラに音を奏でている状態。それぞれの楽器の音は他の楽器に影響されず、独立している。 |
白色化の目的

白色化とは、データの処理方法の一つで、データに含まれる冗長性を取り除き、機械学習のモデルがより学習しやすくなるように整えることを目指します。多くの機械学習モデルは、データの特徴同士の関連性が強いと、学習の効率が悪くなったり、精度が下がったりする傾向があります。白色化は、この特徴同士の関連性をなくすことで、これらの問題を解決し、モデルの性能を高めることが期待できます。
具体的に説明すると、データの各特徴が互いに独立で、かつ同じ程度のばらつきを持つように変換するのが白色化です。例えば、あるデータの中に、互いに強い関連性を持つ特徴があったとします。これらの特徴は本質的には同じ情報を異なる形で表現しているだけで、重複していると言えます。白色化はこのような重複を取り除き、本当に必要な情報だけを残す役割を果たします。
画像認識を例に考えてみましょう。画像データでは、隣り合う画素同士は色の変化が少なく、互いに強い関連性を持っています。そのため、そのままでは学習が難しく、多くの計算資源を必要とします。白色化を適用することで、画素同士の関連性を取り除き、モデルが画像の特徴を捉えやすくします。結果として、学習の効率が上がり、必要な計算資源も抑えることができます。
また、ノイズを多く含むデータに対しても、白色化は有効です。ノイズとは、本来のデータには含まれていない不要な情報のことです。白色化は、このノイズ成分を抑える効果も期待できます。データからノイズを取り除くことで、モデルは本来のデータの特徴をより正確に学習できるようになります。
このように、白色化はデータの前処理として重要な役割を担い、様々な場面で機械学習モデルの性能向上に貢献します。特に、画像認識や音声認識といった分野では、データの次元数が非常に大きく、特徴同士の関連性も高いため、白色化の効果が顕著に現れます。
| 項目 | 説明 |
|---|---|
| 白色化の目的 | データの冗長性を取り除き、機械学習モデルの学習効率と精度を向上させる。特徴同士の関連性をなくす。 |
| 具体的な処理 | データの各特徴が互いに独立で、かつ同じ程度のばらつきを持つように変換する。 |
| 画像認識の例 | 隣り合う画素同士の強い関連性を取り除き、学習効率を上げ、計算資源を抑える。 |
| ノイズへの効果 | ノイズ成分を抑え、モデルが本来のデータの特徴を正確に学習できるようにする。 |
| 効果的な分野 | 画像認識、音声認識など、次元数が大きく、特徴同士の関連性が高いデータ。 |
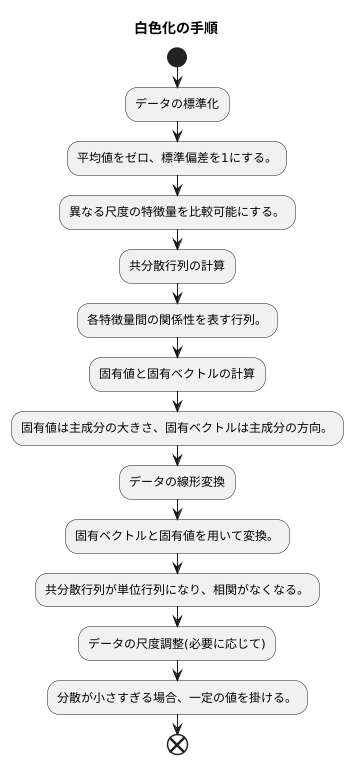
白色化の手順

白色化とは、データの各要素間の相関を取り除き、統計的に独立な状態にするための手法です。これは、データ分析や機械学習において、不要な情報を取り除き、本質的な特徴を捉えるために役立ちます。具体的な手順は以下のとおりです。
まず、データのばらつきを調整するために、各特徴量の平均値をゼロ、標準偏差を1にする標準化を行います。これは、異なる尺度を持つ特徴量を比較可能にするための重要な前処理です。例えば、あるデータセットで身長と体重という二つの特徴量があった場合、身長はセンチメートル単位、体重はキログラム単位で計測されているため、そのままでは直接比較することができません。標準化を行うことで、これらの特徴量を同じ尺度に変換し、比較可能にします。
次に、標準化されたデータの共分散行列を計算します。共分散行列は、各特徴量間の関係性を表す行列であり、対角成分は各特徴量の分散、非対角成分は特徴量間の共分散を表します。この共分散行列から固有値と固有ベクトルを求めます。固有値は、データの主成分の大きさを表し、固有ベクトルは、主成分の方向を表します。
そして、求めた固有値と固有ベクトルを用いて、データの線形変換を行います。具体的には、固有ベクトルを列ベクトルとして並べた行列と、固有値の平方根の逆数を対角成分とする行列を用いて、標準化されたデータを変換します。この変換により、データの共分散行列は単位行列になり、各特徴量間の相関が完全に取り除かれます。つまり、変換後のデータは、互いに独立な成分のみを持つデータとなります。
最後に、必要に応じて、データの尺度を調整します。例えば、白色化後のデータの分散が小さすぎる場合、特定のアルゴリズムの性能に悪影響を与える可能性があります。このような場合は、データ全体に一定の値を掛けることで、分散を調整することができます。
このように、白色化は複数の段階を経て行われます。各段階における処理は、データの特性を適切に変換し、最終的に独立な成分を持つデータを得るために重要な役割を果たします。
白色化と標準化の違い

データの解析を始めるにあたり、前処理は欠かせない手順です。その中でも、標準化と白色化はよく用いられる手法ですが、それぞれ異なる目的と効果を持っています。
まず、標準化について説明します。標準化は、それぞれの変数の平均をゼロ、ばらつきを1にする変換です。例えるなら、様々な長さの棒を全て同じ平均の長さと太さに揃えるようなものです。こうすることで、異なる単位や規模の変数を同じ土俵で比較できるようになります。例えば、身長と体重のように単位が異なるデータでも、標準化によって比較可能になります。標準化は主に、データの尺度を揃え、異なる変数の値の大小関係を適切に扱うために用いられます。
一方、白色化は標準化に加えて、変数同士の関連性をなくす操作を行います。棒の例で言えば、それぞれの棒が互いに影響を与えないように、独立させるイメージです。標準化が個々の棒の長さと太さを揃えるのに対し、白色化はさらに棒の向きを調整し、互いに平行にならないように配置するようなものです。変数間の関連性を取り除くことで、データの構造をより明確に捉えることができます。例えば、複数の変数が互いに強く関連している場合、それらの変数は本質的に同じ情報を表している可能性があります。白色化によってこの関連性をなくすことで、より本質的な情報を抽出しやすくなります。
まとめると、標準化は個々の変数の尺度を調整する手法であり、白色化はさらに変数間の関連性も調整する手法です。前者はデータの比較をしやすくする目的で、後者はデータの構造を明らかにする目的で用いられます。状況に応じて適切な手法を選択することが、データ解析の精度向上に繋がります。
| 手法 | 目的 | 効果 | 例え |
|---|---|---|---|
| 標準化 | データの尺度を揃え、異なる変数の値の大小関係を適切に扱う | 異なる単位や規模の変数を同じ土俵で比較できる | 様々な長さの棒を全て同じ平均の長さと太さに揃える |
| 白色化 | 標準化に加えて、変数同士の関連性をなくす | データの構造をより明確に捉えることができる。本質的な情報を抽出しやすくなる | 標準化に加え、棒の向きを調整し、互いに平行にならないように配置する |
白色化の適用事例

白色化は、様々な分野でデータの質を高める前処理として使われています。まるで写真の現像処理のように、画像や音声、言葉といった様々なデータを加工し、より鮮明で解析しやすい形に変える技術です。
例えば、画像認識の分野を考えてみましょう。カメラで撮影した画像は、そのままでは明るさや色のばらつき、不要な情報が含まれていることがあります。白色化を適用することで、これらのばらつきや不要な情報を抑え、画像本来の特徴を捉えやすくします。特定の物体を認識する際、背景の明るさや色の違いに惑わされずに、物体の形や模様といった重要な特徴に集中できるようになるのです。
音声認識でも白色化は活躍します。録音された音声には、周囲の雑音や反響が含まれており、音声認識の精度を落とす原因となります。白色化を適用することで、これらの雑音や反響を取り除き、クリアな音声信号を得ることができます。これにより、音声認識システムは、話されている言葉をより正確に聞き取ることができるようになります。
自然言語処理の分野では、文章を単語の集まりとして捉え、それぞれの単語を数値のベクトルで表現することがよくあります。しかし、単語ベクトルには、単語同士の関連性による偏りが含まれている場合があります。「大きい」と「巨大」のように似た意味の単語は、ベクトル表現でも近い値を持つ傾向があります。白色化を適用することで、単語間のこうした偏りをなくし、それぞれの単語が持つ本来の意味をより正確に反映したベクトル表現を得ることができます。これにより、文章の意味理解や自動翻訳などの精度向上が期待できます。
このように、白色化は、主成分分析や独立成分分析といった次元削減手法と組み合わせることで、より効果的なデータの前処理を可能にします。様々な分野で活用されている白色化は、データ解析の土台を築き、より高度な分析を可能にする重要な技術と言えるでしょう。
| 分野 | 効果 | 詳細 |
|---|---|---|
| 画像認識 | 明るさや色のばらつき、不要な情報を抑え、画像本来の特徴を捉えやすくする | 背景の明るさや色の違いに惑わされずに、物体の形や模様といった重要な特徴に集中できる |
| 音声認識 | 周囲の雑音や反響を取り除き、クリアな音声信号を得る | 音声認識システムは、話されている言葉をより正確に聞き取ることができる |
| 自然言語処理 | 単語間の偏りをなくし、それぞれの単語が持つ本来の意味をより正確に反映したベクトル表現を得る | 文章の意味理解や自動翻訳などの精度向上 |
白色化の注意点

データの様々な特徴を際立たせるための手法である白色化。しかし、その強力な効果ゆえに、いくつか気を付けなければならない点があります。白色化は、データの持つ個性を際立たせる一方で、隠れていた小さなノイズをも大きくしてしまう可能性があるのです。まるで静かな部屋で小さな音を拾ってしまうマイクのように、データに含まれるわずかなノイズでさえ、白色化によって増幅されて目立つようになってしまうことがあります。もし、元々のデータに多くのノイズが含まれている場合は、白色化によってそのノイズが強調され、本来注目すべき特徴が埋もれてしまうかもしれません。逆に、ノイズがほとんどないデータであれば、白色化によってノイズの影響が弱まり、より鮮明なデータとして分析できることもあります。そのため、白色化を行う前に、データにどの程度のノイズが含まれているのかをしっかりと確認することが重要です。もしノイズが多い場合は、先にノイズを取り除く処理を施すことで、白色化の効果を最大限に引き出すことができます。
また、白色化は複雑な計算を必要とするため、扱うデータの量が多いほど、計算に時間がかかります。膨大なデータに対して白色化を行うと、計算が終わるまでに長い時間を要し、作業全体の効率を下げてしまう可能性があります。限られた時間の中で作業を行う必要がある場合は、データ全体から一部だけを取り出して白色化を行う、あるいはより高速な計算機を使うなど、状況に合わせた工夫が必要です。利用できる計算資源とデータの規模を考慮し、適切な方法を選ぶことが、スムーズな分析につながります。
| 項目 | 説明 |
|---|---|
| 白色化の効果 | データの特徴を際立たせるが、ノイズも増幅する可能性がある |
| ノイズへの影響 | ノイズが多いデータではノイズが強調され、特徴が埋もれる可能性がある。ノイズが少ないデータではノイズの影響が弱まり、鮮明になる。 |
| ノイズ対策 | 白色化前にデータのノイズ量を確認し、多い場合はノイズ除去処理を行う。 |
| 計算コスト | データ量が多いほど計算時間がかかる。 |
| 計算コスト対策 | データの一部を抽出する、高速な計算機を使うなど、状況に合わせた工夫が必要。 |
