シグモイド関数:機械学習の立役者

AIを知りたい
先生、シグモイド関数って、何をするためのものなんですか?

AIエンジニア
簡単に言うと、どんな値でも0から1の間の値に変換してくれる関数だよ。たとえば、色んな大きさの数字がバラバラに入ってきたときに、全部0から1の間にきれいに並べ替えるようなイメージだね。

AIを知りたい
0から1の間の値に変換すると、何が便利なんですか?

AIエンジニア
たとえば、0.5を境にして、0.5以上なら「合格」、0.5未満なら「不合格」みたいに、簡単にグループ分けができるようになるんだ。AIはこういう風に、データをグループ分けして色々なことを判断しているんだよ。
シグモイド関数とは。
人工知能でよく使われる『シグモイド関数』について説明します。この関数は、ロジスティック回帰と呼ばれる予測モデルの結果を計算する際に用いられます。数式で表すと f(x)=11+e-ax(a>0) となり、どんな数字を入力しても、結果は0から1の間の値になります。たとえば、基準値を0.5に設定すると、計算結果が0.5以上であればプラスの例、0.5未満であればマイナスの例として、データを二つのグループに分けることができます。
なめらかな曲線を描く関数

滑らかな曲線を描く関数として、シグモイド関数は数学や情報処理の分野で広く用いられています。グラフに描くと、緩やかな坂道のような、アルファベットのSに似た形をしています。この独特の形状は、入力値の変化に対して出力値が穏やかに変化することを示しています。つまり、急激な変化や飛び跳ねることがなく、連続的に変化するのです。
シグモイド関数の大きな特徴の一つは、入力値を0から1の範囲に収めることです。どんなに大きな値を入力しても、出力値は1に近づくだけで、1を超えることはありません。逆に、どんなに小さな値を入力しても、出力値は0に限りなく近づきますが、0を下回ることはありません。この0から1への変換は、確率や割合を扱う際に非常に便利です。例えば、ある事象が起こる確率を予測する際に、シグモイド関数を用いることで、予測値を確率として解釈することができます。
この関数は、機械学習の分野で、特にニューラルネットワークにおいて重要な役割を果たしています。ニューラルネットワークは、人間の脳の神経回路網を模倣した情報処理モデルです。このモデルでは、シグモイド関数は、各神経細胞(ニューロン)の活性化関数として用いられます。入力信号を受け取ったニューロンは、シグモイド関数を通して出力信号を生成します。この出力信号が次のニューロンへと伝達され、複雑な情報処理が実現されます。シグモイド関数の滑らかな性質は、学習過程の安定化に貢献し、より精度の高い学習を可能にします。また、0から1への出力の制限は、ニューラルネットワークの過剰な反応を抑え、安定した動作を保証する役割も担っています。このように、シグモイド関数は、機械学習の進歩に大きく貢献している、重要な関数と言えるでしょう。
| 特徴 | 説明 |
|---|---|
| 形状 | S字型、滑らかな曲線 |
| 出力値の範囲 | 0から1 |
| 入力値の変化に対する出力値の変化 | 穏やか、連続的 |
| 用途 | 確率や割合の表現、機械学習(ニューラルネットワークの活性化関数) |
| 機械学習における役割 | 学習の安定化、過剰反応の抑制 |
確率の表現に最適

機械学習では、未来の出来事がどれくらい起こりやすいかを予測することがよくあります。例えば、お店に来た人が商品を買うかどうか、受け取った電子手紙が迷惑メールかどうかなど、様々な場面で使われています。この「どれくらい起こりやすいか」を数値で表したものが確率で、0から1の間の値で表されます。0に近いほど起こりにくく、1に近いほど起こりやすいことを意味します。
さて、この確率を予測するために、機械学習では様々な計算方法を使います。その中で、シグモイド関数と呼ばれるものが特に確率の表現に適しています。シグモイド関数は、どんな数値を入力しても、出力される値が必ず0から1の間に収まる性質を持っています。つまり、シグモイド関数の出力値をそのまま確率として扱うことができるのです。
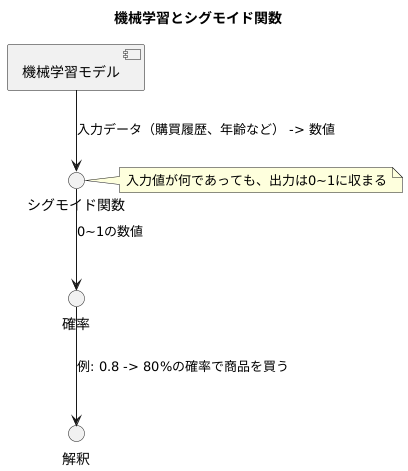
例えば、ある人が商品を買う確率を予測したいとします。機械学習モデルに入力データ(例えば、過去の購買履歴や年齢など)を与えると、モデルは計算を行い、ある数値を出力します。この数値をシグモイド関数に入力すると、0から1の間の値が出力されます。この値を「その人が商品を買う確率」として解釈するのです。もし出力値が0.8だったとしたら、「80%の確率で商品を買う」と予測したと解釈できます。
このように、シグモイド関数は確率を表現するのに非常に便利であり、機械学習の様々な場面で活用されています。シグモイド関数の出力値を確率として解釈することで、予測の精度を高めることができる場合もあります。そのため、機械学習を学ぶ上でシグモイド関数は重要な要素の一つと言えるでしょう。
分類問題で活躍

分け隔てるという作業は、私たちの日常生活でもよく行われています。例えば、洗濯物を色物と白い物に分ける、野菜を種類ごとに仕分けるなど、無意識のうちに行っていることも多いでしょう。コンピュータの世界でも、分け隔てる作業、つまり分類は重要な役割を担っています。これを分類問題と呼びます。
分類問題を解くための強力な道具の一つが、シグモイド関数と呼ばれるものです。これは、入力された値を0から1の間の値に変換する関数です。この0から1の間の値を、ある事象が起こる確率として解釈することで、分類問題を解くことができます。
例えば、写真に写っている動物が猫か犬かを判断する場面を考えてみましょう。この場合、シグモイド関数は、入力された画像データに基づいて、その動物が猫である確率を計算します。もし計算された確率が0.5以上であれば、コンピュータは「猫」と判断し、0.5未満であれば「犬」と判断します。
この0.5という値は、分類の基準となる値であり、閾値と呼ばれています。閾値は問題によって適切な値が異なり、例えば、猫を犬と間違えることよりも、犬を猫と間違えることの方が問題が大きい場合は、閾値を0.5よりも大きく設定することで、猫と判断される確率を高くする、といった調整が可能です。このように、閾値を調整することで、分類の正確さを高めることができます。つまり、シグモイド関数と閾値を組み合わせることで、コンピュータは様々な分類問題を正確に処理することができるのです。
ロジスティック回帰との深い関係

分類問題を解く代表的な手法の一つに、ロジスティック回帰があります。これは、ある出来事が起こる確率を予測する際に用いられる統計的な手法です。例えば、ある人が病気にかかる確率や、ある商品が売れる確率などを予測することができます。このロジスティック回帰という手法を理解する上で、シグモイド関数というものが重要な役割を果たしています。
ロジスティック回帰では、入力されたデータに基づいて計算を行い、その結果を確率として出力します。確率は必ず0から1の間の値をとります。しかし、入力データから直接計算しただけでは、この範囲に収まらない場合があります。そこで、計算結果を0から1の範囲に調整するためにシグモイド関数が用いられます。
シグモイド関数は、入力された値を0から1の間の値に変換する関数です。グラフにすると、緩やかなS字型の曲線を描きます。入力値が小さいときは出力値も0に近く、入力値が大きいときは出力値は1に近づきます。この性質のおかげで、ロジスティック回帰では計算結果を確率として解釈することができるのです。
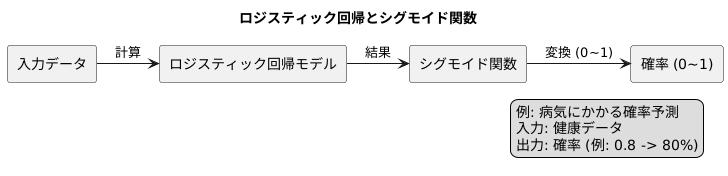
例えば、ある人が病気にかかる確率を予測するモデルを考えてみましょう。様々な健康データを入力として、ロジスティック回帰モデルで計算を行います。計算結果はシグモイド関数によって0から1の値に変換されます。この値が、その人が病気にかかる確率を表します。もし変換された値が0.8だった場合、その人は80%の確率で病気になるという予測になります。
このように、ロジスティック回帰はシグモイド関数と組み合わせて用いられることで、様々な分類問題を解く強力な道具となります。シグモイド関数によって計算結果を確率に変換することで、予測結果を理解しやすく、実用的なものにすることができるのです。
微分の計算も簡単

機械学習では、学習の過程で様々な計算を行います。その中でも、微分という計算は特に重要な役割を担っています。モデルの性能を向上させるためには、適切な調整が必要であり、その調整の際に微分が用いられます。
様々な関数の中で、シグモイド関数は機械学習でよく使われる関数のひとつです。この関数の大きな特徴は、微分の計算が容易である点です。通常、関数を微分すると、元の関数とは全く異なる形になることがよくあります。しかし、シグモイド関数の場合は、微分した結果もシグモイド関数自身を使って表すことができるのです。具体的には、シグモイド関数の値と、1からその値を引いた値を掛け合わせるだけで微分を求めることができます。
このシンプルな計算方法は、機械学習のアルゴリズムにとって大きな利点となります。複雑な微分計算を行う必要がないため、計算にかかる時間や資源を大幅に削減できます。結果として、少ない計算量で精度の高いモデルを構築することが可能になります。また、プログラムも簡潔に書くことができるため、実装や保守も容易になります。このように、シグモイド関数は、計算の効率性とモデルの精度という両方の観点から、機械学習にとって非常に有用な関数と言えるでしょう。
| 項目 | 説明 |
|---|---|
| 微分 | 機械学習のモデル調整に重要な計算 |
| シグモイド関数 | 機械学習でよく使われる関数 |
| シグモイド関数の微分 | シグモイド関数自身で表現可能 (関数値 * (1 – 関数値)) |
| メリット | 計算時間・資源の削減、精度の高いモデル構築、簡潔なプログラム、実装・保守の容易さ |
他の関数との比較

活性化関数には様々な種類があり、それぞれに特徴があります。よく知られているものとして、今回取り上げるシグモイド関数の他に、ステップ関数やReLU関数などがあります。これらの関数を比較することで、シグモイド関数の利点や欠点がより明確になります。
まず、ステップ関数は出力値が0か1のどちらかしか取らないという性質を持っています。これは、白黒をはっきりさせる決定問題などには適していますが、確率のような連続的な値を表現するには不向きです。例えば、明日の降水確率を表現したい場合、ステップ関数では「降る」か「降らない」かのどちらかしか表すことができません。一方、シグモイド関数は0から1の間の連続的な値を取ることができるため、確率を表現するのに適しています。
次に、ReLU関数は0以下の値は0、0より大きい値はそのまま出力する関数です。シグモイド関数に比べて計算が単純であるため、処理速度の向上に貢献します。しかし、ReLU関数には勾配消失問題と呼ばれる問題が発生しやすいという欠点があります。これは、学習の際に勾配が0になってしまうことで、パラメータの更新が停滞し、学習が進まなくなるという問題です。シグモイド関数も勾配消失問題の影響を受けやすい関数ですが、ReLU関数に比べるとその影響は少ないです。
このように、それぞれの活性化関数には長所と短所があります。そのため、問題の性質や要件に応じて適切な関数を選択することが重要です。シグモイド関数は、確率の表現や微分の容易さなど、多くの利点を持つため、様々な場面で利用されています。特に、出力値を確率として解釈したい場合や、勾配消失問題の影響を少なくしたい場合には、シグモイド関数は有効な選択肢となります。
| 活性化関数 | 特徴 | 利点 | 欠点 |
|---|---|---|---|
| ステップ関数 | 出力値が0か1のみ | 白黒はっきりさせる決定問題に適している | 連続的な値を表現するには不向き(例:確率) |
| シグモイド関数 | 出力値が0から1の間の連続的な値 | 確率を表現するのに適している、微分の容易さ、勾配消失問題の影響が少ない | 勾配消失問題の影響を受ける |
| ReLU関数 | 0以下の値は0、0より大きい値はその値を出力 | 計算が単純で処理速度が向上する | 勾配消失問題が発生しやすい |
