ランダムサーチ:機械学習のパラメータ調整

AIを知りたい
先生、「ランダムサーチ」って、結局どういう意味ですか? サイコロを振って決めるみたいに、適当に値を当てはめていくイメージでしょうか?

AIエンジニア
いいところに気がつきましたね。まさに、サイコロを振るように、色々な値を当てはめていく手法です。機械学習では、モデルの性能を決める大切な値(ハイパーパラメータ)がたくさんあります。ランダムサーチは、これらの値をランダム、つまり無作為に決めて、一番良い組み合わせを探す方法です。

AIを知りたい
でも、適当に決めていいんですか? 何か、もっと賢い方法がありそうですが…。

AIエンジニア
もちろん、もっと複雑で賢い方法もあります。しかし、ハイパーパラメータの組み合わせが膨大な場合、一つずつ丁寧に試していくのは途方もない時間がかかります。ランダムサーチは、運任せな面もありますが、意外と早く良い結果が見つかる場合があるんですよ。特に組み合わせが非常に多いときには、有効な手段なんです。
ランダムサーチとは。
人工知能の話でよく出てくる『でたらめ探し』について説明します。でたらめ探しとは、機械学習のモデルを作る際に、うまくいくための設定値(ハイパーパラメータと言います)の組み合わせを見つける方法の一つです。この方法では、設定値の組み合わせを適当に選び、良いモデルができるかどうかを試します。適当に選ぶので、運任せな部分もありますが、実際には設定値の組み合わせが膨大すぎて、他の方法ではとても調べ尽くせない場合に有効なことがあります。
はじめに

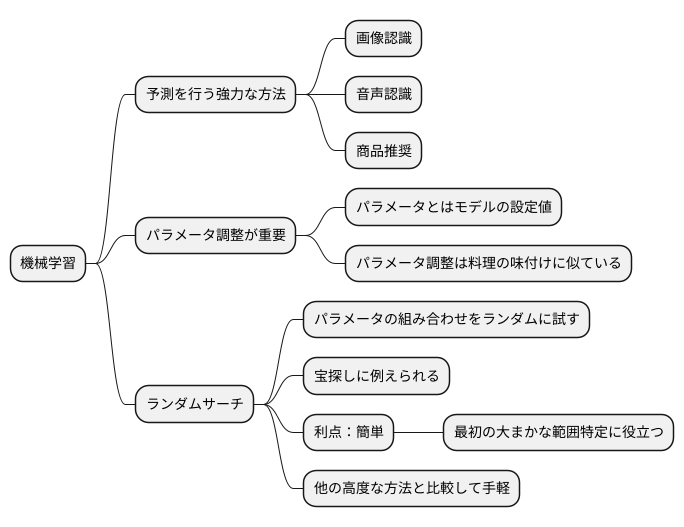
機械学習は、与えられた情報から規則性を見つけ出し、それを基にまだ知らない情報に対して予測を行う、大変強力な方法です。この方法は、画像認識や音声認識、さらには商品の推奨など、様々な分野で活用されています。しかし、機械学習の予測の精度は、機械学習のモデルの様々な設定値、いわゆるパラメータによって大きく左右されます。ちょうど料理の味付けが塩加減や砂糖の量で変わるように、機械学習モデルの性能もパラメータによって大きく変わるのです。
適切なパラメータを見つけることは、機械学習モデルの精度を高める上で非常に重要です。最適なパラメータを見つける作業は、まるで宝探しのようなものです。広大な砂漠の中から、貴重な宝石を探し出すようなものです。この宝探しを効率的に行うための方法の一つが、ランダムサーチと呼ばれる手法です。
ランダムサーチは、その名前の通り、パラメータの組み合わせをランダムに選び、その組み合わせでどのくらい良い予測ができるかを試す方法です。地図を持たずに、砂漠のあちこちをランダムに掘ってみるようなものです。一見非効率的に思えるかもしれませんが、意外と効果的な場合が多いのです。特に、パラメータの種類が多く、最適な組み合わせがどこにあるのか全くわからない場合、ランダムサーチは有効な手段となります。
他の、もっと複雑で洗練されたパラメータ調整の方法もありますが、ランダムサーチは比較的簡単に実行できるという利点があります。高度な方法の中には、複雑な計算が必要なものもあり、時間もかかります。それに比べて、ランダムサーチは手軽に試すことができるため、最初の段階で最適なパラメータの大まかな範囲を絞り込むのに役立ちます。まるで、砂漠のどのあたりに宝石が埋まっているのか、大まかな見当をつけるようなものです。このように、ランダムサーチはシンプルながらも効果的なパラメータ調整の手法として、広く利用されています。
ランダムサーチの仕組み

ランダムサーチは、機械学習モデルの最適な設定値を見つけるための手法の一つです。この手法は、名前の通り、設定値の候補を無作為に選び出すというシンプルな仕組みです。
具体的には、まず、各設定項目に対して探索範囲を定めます。例えば、学習率であれば「0.001から0.1まで」、重みの初期値の範囲であれば「-1から1まで」といった具合です。そして、これらの範囲内で、それぞれの設定値を乱数を使って選び出します。
例えば、学習率が0.001から0.1の間、正則化の強さが0.01から1の間と設定した場合、ランダムサーチは、0.0052のような学習率と、0.35のような正則化の強さを無作為に選択します。
このようにして選ばれた設定値を使って、実際に機械学習モデルの学習を行い、その性能を評価します。この一連の流れを何度も繰り返し、最も高い性能を示した設定値の組み合わせを最終的に採用します。試行回数は、計算資源や時間に応じて自由に設定できます。
ランダムサーチの大きな利点は、実装が容易である点です。複雑な計算やアルゴリズムを必要としないため、比較的簡単にプログラムを書くことができます。また、計算量も少なくて済むため、広大な探索空間を持つ問題に対しても適用できます。さらに、探索範囲全体を満遍なく探索する性質があるため、特定の範囲に偏ることなく、より良い設定値を見つけられる可能性があります。これは、設定値の良し悪しが複雑に絡み合っている場合に特に有効です。
一方で、ランダムサーチは、設定値を選ぶ際に規則性がないため、無駄な探索をしてしまう可能性も秘めています。より効率的に最適な設定値を見つけたい場合は、他の手法も検討する必要があります。
| 手法 | ランダムサーチ |
|---|---|
| 仕組み | 設定値の候補を無作為に選び出す |
| 手順 | 1. 各設定項目の探索範囲を定める 2. 範囲内で乱数を使って設定値を選び出す 3. 選ばれた設定値でモデル学習・評価 4. 複数回繰り返し、最も高性能の設定値を採用 |
| 利点 | 実装が容易 計算量が少ない 探索範囲全体を満遍なく探索 |
| 欠点 | 無駄な探索をする可能性がある |
利点と欠点

無作為に探すやり方には、良い点と悪い点があります。まず良い点としては、分かりやすく手軽に使えることが挙げられます。たくさんの計算を必要とせず、同時にいくつもの作業を進めるのにも向いているため、大きなデータの集まりや複雑な模型にも使えます。また、探す範囲全体をくまなく調べるので、一番良い結果に見えるけれど実はもっと良い結果がある、といった状況に陥りにくいのも特徴です。
しかし、無作為に探すやり方には、一番良い設定を見つけるまでにたくさんの回数試す必要があるという悪い点もあります。きっちりと順序立てて探すやり方と違って、探す範囲を規則的に調べるわけではないので、一番良い設定の近辺をうまく探せないかもしれません。具体的に言うと、設定の組み合わせを規則的に変えて試していく方法と比べると、無作為に探す方法は非効率です。なぜなら、規則的に探す方法は、ある設定を試した結果をもとに、次の設定を賢く選ぶことができるからです。一方、無作為に探す方法は、常に設定をランダムに選ぶため、既に試した結果を活かすことができません。また、既に良い設定が見つかっている場合、それ以上の設定を見つけるのが難しいという欠点もあります。なぜなら、無作為に設定を選ぶため、良い設定の周辺を集中的に探索することができないからです。
とはいえ、探す範囲がとても広く、一番良い設定がどこにあるか全く分からない場合には、無作為に探すやり方は役に立つと言えるでしょう。特に、計算資源が限られている場合や、時間的な制約が厳しい場合には、無作為に探すやり方が有効な選択肢となります。なぜなら、他の方法と比べて少ない計算量で、比較的良い解を見つけることができるからです。また、並列計算にも容易に適用できるため、計算時間を大幅に短縮することができます。このように、無作為に探すやり方には、状況によっては大きな利点があります。
| 項目 | 内容 |
|---|---|
| 良い点 |
|
| 悪い点 |
|
| 利点がある状況 |
|
他の手法との比較

様々な手法の長所と短所を把握し、適切なものを選ぶことは、機械学習モデルの性能向上に欠かせません。ここでは、代表的なパラメータ調整手法であるランダムサーチと、他の手法との違いを詳しく見ていきましょう。
まず、網羅的な探索を行うグリッドサーチは、設定した範囲のすべてのパラメータの組み合わせを試します。そのため、指定した範囲の最適なパラメータを見つけることができます。しかし、パラメータの種類や範囲が広くなると、組み合わせの数が爆発的に増え、膨大な計算時間を要するという欠点があります。例えば、5つのパラメータがあり、それぞれに10通りの値を設定すると、10の5乗、つまり10万通りの組み合わせを試すことになります。
次に、ベイズ最適化は、過去の試行結果を基に、次に試すパラメータを確率的に選択する手法です。この手法は、グリッドサーチに比べて効率的に最適なパラメータを見つけられる可能性が高く、少ない試行回数で良い結果が期待できます。しかし、ベイズ最適化は、複雑な計算が必要となるため、実装の難易度が高く、計算時間も長くなる可能性があります。また、過去の試行結果に影響されるため、探索範囲が限定され、真の最適なパラメータを見逃してしまう可能性も懸念されます。
最後に、ランダムサーチは、指定した範囲からパラメータをランダムに選択し、試行を繰り返す手法です。グリッドサーチやベイズ最適化に比べて、実装が非常に簡単で、計算時間も短いという利点があります。また、広範囲のパラメータ空間を探索できるため、思いがけない良いパラメータが見つかる可能性もあります。ランダムサーチは、他の手法に比べて必ずしも最適なパラメータを見つけられるとは限りませんが、その手軽さと効率の良さから、多くの場合で最初の選択肢として選ばれます。特に、時間や計算資源が限られている場合、あるいは最適なパラメータを求めるよりも、まずはある程度の性能を持つモデルを早く作りたい場合に有効です。
| 手法 | 長所 | 短所 |
|---|---|---|
| グリッドサーチ | 指定した範囲の最適なパラメータを見つけることができる | パラメータの種類や範囲が広くなると、計算時間が膨大になる |
| ベイズ最適化 | グリッドサーチより効率的に最適パラメータを見つけられる可能性が高い。少ない試行回数で良い結果が期待できる。 | 実装が難しい。計算時間が長くなる可能性がある。探索範囲が限定され、真の最適パラメータを見逃す可能性がある。 |
| ランダムサーチ | 実装が簡単。計算時間が短い。広範囲のパラメータ空間を探索できる。 | 必ずしも最適なパラメータを見つけられるとは限らない。 |
まとめ

機械学習の模型を作る際には、模型の働きを左右する様々な数値を決める必要があります。これらの数値を適切に調整することを「パラメータ調整」と呼びます。パラメータ調整の方法の一つに、ランダムサーチと呼ばれる手法があります。
ランダムサーチは、名前の通りパラメータの値を無作為に選び、その時の模型の性能を評価する方法です。広大な数値の組み合わせの中から、宝探しのように手探りで良い値を探し出すイメージです。特に、最適なパラメータがどこにあるか全く見当もつかない場合、ランダムサーチは有効な手段となります。なぜなら、他の手法のように特定の範囲に絞って探索するのではなく、あらゆる可能性を平等に試すからです。
ランダムサーチの大きな利点は、計算の手間が少ないことです。他の複雑な調整方法と比べて、理解しやすく、簡単にプログラムに組み込むことができるため、気軽に試すことができます。また、計算に時間がかからないので、短時間で結果を得たい場合にも役立ちます。
もちろん、ランダムサーチにも限界はあります。無作為に探すため、たまたま良い値が見つかるかどうかは運次第という側面があります。また、他の手法と比べて、必ずしも最高の性能が出るとは限りません。
より精度の高い調整方法としては、数値を規則的に変化させて試すグリッドサーチや、過去の結果を学習して効率的に探索するベイズ最適化などがあります。これらの手法は、ランダムサーチよりも計算に時間がかかることもありますが、より良いパラメータを見つける可能性が高くなります。
どの調整方法が最適かは、扱うデータや模型の種類によって異なります。そのため、様々な方法を試してみて、自分の課題に最も適した方法を選ぶことが大切です。
| 手法 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| ランダムサーチ | パラメータの値を無作為に選び、模型の性能を評価する。 | 計算の手間が少ない、理解しやすい、短時間で結果を得られる | 運次第、必ずしも最高の性能が出るとは限らない |
| グリッドサーチ | 数値を規則的に変化させて試す。 | ランダムサーチより良いパラメータを見つける可能性が高い | 計算に時間がかかる場合がある |
| ベイズ最適化 | 過去の結果を学習して効率的に探索する。 | ランダムサーチより良いパラメータを見つける可能性が高い | 計算に時間がかかる場合がある |
