RAE:誤差を測る新たな視点

AIを知りたい
先生、「RAE」ってなんですか?

AIエンジニア
RAEは「相対絶対誤差」のことで、機械学習モデルの予測精度を評価する方法の一つだよ。簡単に言うと、実際の値と予測値のズレを、実際の値の大きさで割ったものと言えるね。

AIを知りたい
実際の値の大きさで割るというのは、どういうことですか?

AIエンジニア
例えば、1000円と予測して、実際は900円だった場合と、10円と予測して実際は0円だった場合を考えてみよう。どちらも誤差は100円だけど、1000円に対する100円と10円に対する100円では、相対的な誤差の大きさが違うよね?RAEは、そうした違いを捉えることができるんだ。
RAEとは。
「人工知能に関わる言葉、『相対絶対誤差』(統計学や機械学習で使われる、予測値と正解値のずれを評価する数値、もしくはそれを計算する手順のことです。ずれの大きさを、正解値との比率で表したものと言えます。こうすることで、正解値の範囲が異なるデータ同士でも、評価値を比べやすくなるという利点があります。)について」
相対絶対誤差とは

相対絶対誤差(そうたいぜったいごさ)は、統計学や機械学習の分野で予測の正確さを評価する際に使われる大切な指標です。この指標は、実測値と予測値の差を、実測値の平均値で割ることで計算されます。この計算方法のおかげで、異なる単位や規模を持つデータでも比較が可能になります。例えば、家の値段と株価の予測のように、全く異なる種類のデータを扱う場合でも、相対絶対誤差を用いることで、予測の精度を同じ尺度で比べることができます。
相対絶対誤差を理解する上で重要なのは、この指標が「相対的」な誤差を表している点です。つまり、単に予測値と実測値の差を見るだけでなく、実測値の平均値に対する割合で誤差を評価します。これは、ある程度予想される誤差の範囲を考慮に入れるようなものです。例えば、100万円の家を予測する際に1万円の誤差と、10万円の株を予測する際に1万円の誤差では、同じ1万円でも意味合いが大きく違います。相対絶対誤差は、このような違いを適切に反映することができます。
相対絶対誤差の値は、通常0から1までの範囲で表されます。0に近い値は、予測値が実測値と非常に近い、つまり予測精度が高いことを示します。逆に1に近い値、あるいは1を超える値は、予測値と実測値の間に大きなずれがあることを意味し、予測精度が低いことを示します。このように、相対絶対誤差は、予測モデルの良し悪しを判断するための分かりやすい指標となっています。
相対絶対誤差は、モデルの改善にも役立ちます。誤差の値を確認することで、モデルの弱点や改善点を把握することができます。例えば、特定の条件下で誤差が大きくなる場合、その条件に特化した修正を加えることで、モデル全体の精度を向上させることができます。このように、相対絶対誤差は、予測モデルの開発や改良において欠かせないツールと言えるでしょう。
| 指標名 | 説明 | 計算方法 | 値の範囲 | 解釈 | 用途 |
|---|---|---|---|---|---|
| 相対絶対誤差 | 予測の正確さを評価する指標。異なる単位や規模のデータでも比較可能。実測値の平均値に対する割合で誤差を評価する「相対的」な誤差。 | (実測値 – 予測値) / 実測値の平均値 | 0 ~ 1 (1以上になる場合もある) | 0に近い値は予測精度が高い。1に近い値、または1を超える値は予測精度が低い。 | 予測モデルの良し悪しを判断、モデルの改善点を把握。 |
計算方法

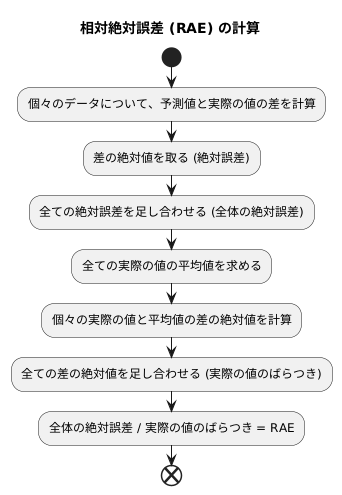
相対絶対誤差(RAE)は、予測の正確さを評価するための指標で、計算方法は比較的分かりやすいです。まず、個々のデータについて、予測値と実際の値の差を計算します。この差は、正負の値を持つ可能性があるので、その絶対値を取ります。これは絶対誤差と呼ばれ、予測がどれだけ実際の値からずれているかを表します。次に、これらの絶対誤差を全て足し合わせます。これは、全体の予測誤差の大きさを示します。
しかし、この全体の誤差だけを見ても、予測の良さを評価するには不十分です。なぜなら、元のデータの値が大きい場合には、誤差も大きくなる傾向があるからです。そこで、RAEでは、この誤差を、実際の値のばらつき具合で割ることで、相対的な誤差を計算します。
実際の値のばらつき具合は、次のように計算します。まず、全ての実際の値の平均値を求めます。次に、個々の実際の値とこの平均値との差の絶対値を計算し、それらを全て足し合わせます。これは、実際の値が平均値からどれくらいばらついているかを表す指標となります。
最後に、全体の絶対誤差の合計を、この実際の値のばらつきの合計で割ります。この結果がRAEとなり、0から1の間の値を取ります。RAEの値が0に近いほど、予測値と実際の値が近く、予測の精度が高いことを示します。逆に、RAEの値が1に近いほど、予測値と実際の値のずれが大きく、予測の精度が低いことを意味します。
RAEを使う利点は、異なるデータセット間で予測精度を比較できる点にあります。元のデータの大きさに関係なく、相対的な誤差を評価できるため、異なるスケールのデータでも比較が可能です。例えば、1000円単位の販売額の予測と、1円単位の価格の予測の精度を比較する場合でも、RAEを用いることで公平な評価ができます。
利点と欠点

相対絶対誤差(RAE)には、長所と短所があります。まず、長所を見ていきましょう。RAEの大きな利点は、規模に左右されないことです。つまり、異なる規模のデータ群を比べたいときにも、RAEを使えば簡単に比較ができます。例えば、ある製品の売上高と、別の製品の出荷数を比べたい場合、それぞれの規模が大きく違っても、RAEを使えば比較が可能です。また、計算方法がとても簡単なのも、RAEの優れた点です。複雑な計算式を覚える必要がなく、誰でも簡単に計算できます。さらに、RAEの値は常に0から1の間におさまります。そのため、モデルの良し悪しを直感的に理解しやすいです。値が0に近いほど、予測の精度が高いことを示し、1に近いほど精度が低いことを示します。
一方、RAEには短所も存在します。特に注意が必要なのは、実際の値が0に近い場合です。RAEは実際の値を分母に持つため、この値が0に近づくと、RAEの値が非常に大きくなってしまう可能性があります。これは、まるで小さな虫眼鏡で太陽の光を集めるように、小さな値が大きな誤差を生み出すことに似ています。このような場合、RAEはモデルの性能を正しく評価できません。また、RAEは外れ値、つまり極端に大きな、あるいは小さな値の影響を受けやすいという欠点もあります。例えば、ほとんどのデータが0に近い値をとっているにもかかわらず、一つだけ非常に大きな値を持つデータがあると、RAEはこの外れ値に引っ張られて、大きな値になってしまいます。これは、まるで静かな湖面に小石を投げ入れると、波紋が広がるように、一つの外れ値が全体の評価を歪めてしまうのです。このように、RAEにはいくつかの短所があるため、これらの短所を理解した上で、状況に応じて適切に利用することが大切です。
| 項目 | 説明 |
|---|---|
| 長所 |
|
| 短所 |
|
他の指標との比較

予測の正確さを評価する指標は数多くありますが、それぞれに特徴があり、用途に応じて使い分けることが重要です。よく用いられる指標として、平均絶対誤差(MAE)、平均二乗誤差(MSE)、そして今回ご紹介する平均絶対相対誤差(RAE)があります。これらの指標を比較することで、RAEの利点が見えてきます。
MAEは、予測値と実測値の差の絶対値を平均したものです。MAEは、誤差の大きさを直感的に理解しやすいという利点があります。RAEと同様に、単位の影響を受けないため、異なる単位のデータでも比較が可能です。しかし、MAEは実測値に対する誤差の割合を示していないため、異なるデータセット間での比較は難しい場合があります。例えば、平均値が100と1000のデータセットでは、同じMAEの値でも、相対的な誤差の大きさは異なります。
一方、MSEは、予測値と実測値の差を二乗して平均したものです。MSEは、大きな誤差をより強く罰するという特徴があります。つまり、外れ値の影響を受けやすい指標です。また、MSEは単位の影響を受けるため、異なる単位のデータセット間での比較には適していません。例えば、メートルで計測したデータとキロメートルで計測したデータでは、MSEの値が大きく異なるため、単純な比較はできません。
RAEは、MAEを実際の値で割ることで、相対的な誤差を計算します。これにより、異なるデータセット間でも比較が可能になります。つまり、RAEは、実測値のスケールに関係なく、誤差の大きさを相対的に評価できます。これは、平均値が大きく異なるデータセットを比較する際に特に有用です。例えば、住宅価格と株価のように、スケールの異なるデータセットを比較する場合、RAEを用いることで、より適切な評価が可能になります。このように、RAEは、異なるデータセット間で予測精度を比較する必要がある場合に、非常に有効な指標と言えるでしょう。
| 指標 | 計算方法 | 特徴 | 利点 | 欠点 |
|---|---|---|---|---|
| MAE (平均絶対誤差) | 予測値と実測値の差の絶対値を平均 | 誤差の大きさを直感的に理解しやすい、単位の影響を受けない | 異なる単位のデータでも比較可能 | 実測値に対する誤差の割合を示していないため、異なるデータセット間での比較は難しい |
| MSE (平均二乗誤差) | 予測値と実測値の差を二乗して平均 | 大きな誤差をより強く罰する | – | 外れ値の影響を受けやすい、単位の影響を受けるため、異なる単位のデータセット間での比較には適していない |
| RAE (平均絶対相対誤差) | MAEを実測値で割る | 実測値のスケールに関係なく、誤差の大きさを相対的に評価できる | 異なるデータセット間でも比較が可能 | – |
まとめ

予測の正確さを測る尺度の一つに、平均絶対誤差率というものがあります。これは、よくRAEと略されます。この尺度は、統計学や機械学習といった分野で、作った予測の模型がどれくらい当たるのかを確かめる際に、よく使われます。
RAEの大きな利点は、数値の大きさに左右されないという点です。例えば、りんごの値段の変動を予測する模型と、住宅価格の変動を予測する模型を比べたいとします。りんごの値段は数百円単位で変動する一方、住宅価格は数千万円単位で変動します。このような場合、単純な誤差を比較しても意味がありません。RAEは、それぞれの数値の平均値に対する誤差の割合を見るため、異なる種類のデータでも比較が可能になります。また、計算方法も単純で分かりやすいので、手軽に利用できます。
しかし、RAEには弱点もあります。もしも実際の値がゼロに近い場合、誤差の割合が非常に大きくなってしまい、正しく評価できません。また、極端に大きな値や小さな値、いわゆる外れ値の影響を受けやすいという欠点もあります。例えば、ほとんどのデータが100前後の値をとる中で、一つだけ10000という値があると、この値がRAEに大きな影響を与えてしまうのです。
このように、RAEには利点と欠点の両方があります。だからこそ、データの特徴や分析の目的に合わせて、RAEを使うべきかどうか、慎重に判断する必要があります。RAEは、ただ誤差を測るだけでなく、データに隠された関係性を理解し、より精度の高い予測模型を作るための道具となるでしょう。これからの時代、データをうまく活用することがますます大切になります。RAEのような指標を正しく理解し、使いこなせるようになれば、データ分析の質をさらに高めることができるでしょう。
| 項目 | 内容 |
|---|---|
| 名称 | 平均絶対誤差率 (RAE) |
| 分野 | 統計学、機械学習 |
| 目的 | 予測モデルの精度評価 |
| 利点 | 数値の大きさに左右されない、計算が単純 |
| 欠点 | 実際の値がゼロに近い場合、誤差の割合が非常に大きくなる、外れ値の影響を受けやすい |
| 注意点 | データの特徴や分析の目的に合わせて、RAEを使うべきかどうか、慎重に判断する必要がある |
