中央絶対誤差:機械学習での活用

AIを知りたい
先生、「中央絶対誤差」ってどういう意味ですか?よくわからないです。

AIエンジニア
そうだね、少し難しいよね。「中央絶対誤差」は、簡単に言うと、たくさんのデータの誤差の絶対値の中央値のことだよ。たとえば、10個のデータがあって、それぞれの誤差の絶対値を小さい順に並べたとき、5番目と6番目の値の平均が中央絶対誤差になるんだ。

AIを知りたい
誤差の絶対値の中央値…ですか? なぜ普通の平均値ではなく、絶対値の中央値を使うのですか?

AIエンジニア
いい質問だね。外れ値と呼ばれる、極端に大きな誤差があるデータに影響されにくいからなんだ。平均値だと、大きな外れ値があると、その値に引っ張られて全体の誤差が大きく見えてしまう。中央絶対誤差は、そのような外れ値の影響を受けにくいので、より実態に近い誤差を捉えることができるんだよ。
中央絶対誤差とは。
人工知能でよく使われる言葉である「中央絶対誤差」について説明します。中央絶対誤差は、機械学習の分野で用いられるものです。ちなみに、誤差は「予想した値 - 本当の値」で計算しても、「本当の値 - 予想した値」で計算しても構いません。
中央絶対誤差とは

中央絶対誤差は、機械学習モデルの良し悪しを測る物差しの一つです。この物差しは、予測値と正解値の差を基に計算されます。具体的には、幾つかのデータそれぞれについて、予測値と正解値がどれくらい離れているかを調べます。それぞれの差を正の値に変換し、それらを大きさの順に並べます。そして、ちょうど真ん中に来る値が中央絶対誤差です。
中央絶対誤差を使う大きな利点は、極端に大きな誤差があるデータの影響を受けにくいことです。例えば、ほとんどのデータで予測値と正解値の差が1程度だったとしても、一つだけ差が100もあるデータがあるとします。この場合、差の平均値は10近くになり、モデルの性能が実際よりも悪く見えてしまいます。しかし、中央絶対誤差では、真ん中の値を見るので、極端な値に引きずられることなく、真の性能に近い値を得られます。
中央絶対誤差と似た指標に平均絶対誤差というものがあります。これは、全ての誤差の平均値をとる物差しです。平均絶対誤差は計算が簡単ですが、先ほど説明したように、極端な値に影響されやすい欠点があります。10個のデータのうち、9個の誤差が1で、1個が100の場合を考えると、平均絶対誤差は約10になりますが、中央絶対誤差は1のままです。このように、外れ値が含まれている可能性がある場合は、中央絶対誤差の方がより信頼できる指標と言えます。
中央絶対誤差は、モデルの典型的な誤差を捉えるのに役立ちます。つまり、多くのデータでどれくらいの誤差が出ているかを把握するのに適しています。ただし、誤差の全体像を把握したい場合は、他の指標も併せて見るのが良いでしょう。中央絶対誤差はあくまでも一つの指標であり、それだけで全てを判断することはできません。様々な指標を組み合わせて使うことで、より深くモデルの性能を理解することができます。
| 指標名 | 計算方法 | 長所 | 短所 | 備考 |
|---|---|---|---|---|
| 中央絶対誤差 | 予測値と正解値の差の絶対値を並べ、中央値をとる | 外れ値の影響を受けにくい | 誤差の全体像を把握しにくい | モデルの典型的な誤差を捉えるのに役立つ |
| 平均絶対誤差 | 予測値と正解値の差の絶対値の平均をとる | 計算が簡単 | 外れ値の影響を受けやすい |
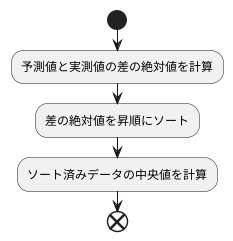
計算方法

計算方法は、中央絶対誤差を求める手順を踏みます。この計算は比較的簡単で、大きく分けて三つの段階に分かれます。
まず最初の段階では、それぞれのデータについて、予測値と正解値の差を計算します。この時、差が正の値でも負の値でも、常に正の値に変換する必要があります。例えば、予測値が10で正解値が8の場合、その差は2となります。逆に、予測値が8で正解値が10の場合、差は-2となりますが、これを正の値である2に変換します。このようにして、全てのデータについて、予測値と正解値の差の絶対値を計算します。
次の段階では、一つ前の段階で計算した絶対値を小さい順に並べ替えます。例えば、計算した絶対値が5、2、8、1、4の場合、小さい順に並べ替えると1、2、4、5、8となります。
最後の段階では、並べ替えた値の中から中央値を探します。データの個数が奇数の場合、中央値はちょうど真ん中の値になります。例えば、1、2、4、5、8と5つのデータがある場合、真ん中の値である4が中央値となります。一方、データの個数が偶数の場合、中央値は真ん中の二つの値の平均になります。例えば、1、2、4、5と4つのデータがある場合、真ん中の二つの値は2と4なので、その平均である(2+4)÷2=3が中央値となります。
このようにして計算された中央値は、外れ値の影響を受けにくいという特徴を持っています。つまり、極端に大きな誤差や小さな誤差があっても、それらに左右されずに、データ全体の中心的な誤差の大きさを示すことができます。そのため、データのばらつき具合をより正確に捉えるのに役立ちます。
他の指標との比較

様々な指標が存在する中で、予測値と実際の値との差、つまり誤差を測る方法は数多くあります。その中で、中央絶対誤差は、平均絶対誤差や平均二乗誤差といった他の指標と比べて、突出した値の影響を受けにくいという特徴を持っています。
まず、平均絶対誤差について考えてみましょう。これは、それぞれの誤差の絶対値を全て足し合わせ、データの数で割ることで計算されます。全ての誤差を平等に扱うため、もし極端に大きな誤差が一つでも存在すると、全体の平均値が引っ張られてしまいます。つまり、突出した値に影響されやすい指標と言えるでしょう。
次に、平均二乗誤差を見てみます。これは、それぞれの誤差を二乗した値を全て足し合わせ、データの数で割ることで計算されます。誤差を二乗するため、平均絶対誤差よりもさらに突出した値の影響を強く受けます。大きな誤差は二乗することでさらに大きくなり、平均値を大きく押し上げてしまうからです。
これに対し、中央絶対誤差は、誤差の大きさのちょうど真ん中の値を使用します。そのため、いくつか突出した値があったとしても、中央値はほとんど影響を受けません。データ全体を順番に並べたときに、真ん中に位置する値を見るため、少数の極端な値に左右されることなく、誤差の全体像を把握できるのです。
このように、中央絶対誤差は、データの中に突出した値がいくつか含まれている場合でも、安定した評価をすることができます。データの分布に偏りがある場合や、突出した値が予測に大きな影響を与えてしまうことを避けたい場合に、特に役立つ指標と言えるでしょう。
| 指標 | 計算方法 | 突出した値の影響 |
|---|---|---|
| 平均絶対誤差 | 誤差の絶対値の平均 | 影響されやすい |
| 平均二乗誤差 | 誤差の二乗の平均 | 非常に影響されやすい |
| 中央絶対誤差 | 誤差の絶対値の中央値 | 影響されにくい |
活用事例

活用事例は多岐に渡ります。機械学習の様々な場面で、中央絶対誤差は役立ちます。特に、予測を行うタスクで、データの中に大きく外れた値が混ざっている場合に力を発揮します。例えば、人の収入や家の値段を予測するといった場面です。これらのデータには、とびぬけて高額な家や、ごく一部の非常に高い収入といった、外れた値が含まれることがよくあります。このような外れた値があると、平均を使った誤差の計算方法では、予測の正確さを正しく測ることができません。平均は外れた値に引っ張られてしまうからです。中央絶対誤差を使うと、このような外れた値の影響を少なくして、予測の真の正確さを測ることができます。
中央絶対誤差は、外れた値を見つけるためにも役立ちます。通常と異なるデータを見つけることを異常値検知といいますが、この分野でも中央絶対誤差が活躍します。中央絶対誤差を使うことで、データがどれくらい普通の値から外れているかを測ることができます。このずれの大きさを基準にして、通常と異なるデータを効率よく見つけることが可能になります。
例えば、製造業における製品の品質管理を考えてみましょう。製品の寸法や重さといったデータに、不良品による異常値が混入することがあります。このような場合、中央絶対誤差を用いることで、不良品を効率的に検出し、品質の低下を未然に防ぐことができます。また、金融業界では不正な取引の検出に役立ちます。取引金額や頻度といったデータから、通常と異なるパターンを検出し、不正行為の早期発見に繋がります。このように、中央絶対誤差は様々な分野で、データの質を保ち、正確な予測を行うために欠かせない役割を担っています。
| 活用事例 | 説明 | 例 |
|---|---|---|
| 予測タスク(外れ値がある場合) | 外れ値の影響を受けにくく、予測の正確さを正しく測れる。 | 人の収入や家の値段の予測 |
| 異常値検知 | データのずれを測り、通常と異なるデータを効率よく見つける。 |
|
限界

中央絶対誤差は、機械学習モデルの性能を測る指標として、頑健性が高いことで知られています。つまり、外れ値のような極端な値の影響を受けにくいという利点があります。これは、誤差の絶対値の中央値を見るという性質によるものです。しかし、この指標には限界も存在します。
第一に、中央絶対誤差は中央値のみを考慮するため、誤差の分布全体を捉えきれません。中央値が同じであっても、誤差のばらつきが大きい場合と小さい場合では、モデルの性能は異なってきます。例えば、あるモデルは誤差が0に近い値に集中している一方で、別のモデルは誤差が大きくばらついているとします。中央絶対誤差は同じ値を示すかもしれませんが、ばらつきの小さいモデルの方が安定した予測ができると言えるでしょう。このようなばらつきを把握するためには、標準偏差や四分位範囲といった他の指標も併用する必要があります。
第二に、中央絶対誤差は微分不可能な関数です。微分不可能とは、滑らかな曲線で表すことができず、ある点における傾きが定義できないことを意味します。多くの機械学習モデルは、勾配降下法と呼ばれる最適化手法を用いて訓練されます。この手法は、関数の傾きを利用して最適なパラメータを探すため、微分不可能な関数を直接最適化することはできません。そのため、モデルの訓練時には、平均二乗誤差などの微分可能な損失関数を用いることが一般的です。そして、訓練後のモデルの評価指標として中央絶対誤差を用います。
最後に、中央絶対誤差は誤差の絶対値の中央値を見るため、誤差の正負の情報は無視されます。つまり、モデルの予測値が実際の値よりも常に大きい、あるいは常に小さいといった系統的な傾向を捉えることができません。例えば、あるモデルは常に実際の値よりも高い値を予測し、別のモデルは常に低い値を予測するとします。これらのモデルの誤差の絶対値が同じであれば、中央絶対誤差は同じ値を示します。しかし、これらのモデルは異なる性質を持っており、改善のためのアプローチも異なります。このような偏りを検出するためには、平均誤差などの他の指標と組み合わせて使用することが重要です。
| メリット | デメリット | 補足説明 |
|---|---|---|
| 頑健性が高い(外れ値の影響を受けにくい) | 誤差の分布全体を捉えきれない | 中央値のみを考慮するため、ばらつきが大きい場合と小さい場合を区別できない。標準偏差や四分位範囲も併用する必要がある。 |
| 微分不可能 | 勾配降下法による最適化ができないため、モデル訓練時は他の損失関数(例:平均二乗誤差)を使用し、評価指標として用いる。 | |
| 誤差の正負を無視する | 予測値が常に大きい/小さいといった系統的な傾向を捉えられない。平均誤差などの指標と組み合わせて使用することが重要。 |
まとめ

機械学習のモデルを評価する際に、予測値と実際の値のズレ具合を測ることはとても大切です。ズレの大きさを表す指標は数多くありますが、その中で中央絶対誤差は、外れ値、つまり極端に大きな値や小さな値の影響を受けにくいという優れた点があります。たとえば、ほとんどのデータは予測値と近い値を示しているのに、一部のデータだけが大きく外れているような場合、平均を用いた指標ではその外れ値に引っ張られて、モデルの本当の性能を見誤ってしまうことがあります。中央絶対誤差は、このような外れ値に左右されずに、データ全体の中央のズレ具合を捉えるため、より信頼性の高い評価を可能にします。
しかし、中央絶対誤差にも限界はあります。ズレの全体像を捉えることが難しいという点が一つです。中央値はデータの中央の値しか見ないため、ズレの分布全体や、どれだけのデータがどれくらいずれているのかといった詳しい情報は分かりません。また、中央絶対誤差は微分ができないという数学的な特性も持ちます。そのため、微分を使った最適化手法を用いることが難しく、モデルの学習過程で直接的にこの指標を最小化することはできません。さらに、ズレが正の値か負の値かといったズレの方向性を無視することも中央絶対誤差の特性です。予測値が常に実際の値よりも大きいか小さいかといった情報は、この指標からは読み取れません。
このように、中央絶対誤差には長所と短所の両方があります。そのため、中央絶対誤差だけでモデルを評価するのではなく、他の指標も組み合わせて使うことが大切です。平均絶対誤差や平均二乗誤差といった他の指標と併用することで、より多角的にモデルの性能を評価し、より精度の高い機械学習モデルを作ることが可能になります。状況に応じて適切な指標を選び、それぞれの特性を理解した上で活用することが重要です。
| 指標 | 長所 | 短所 |
|---|---|---|
| 中央絶対誤差 | 外れ値の影響を受けにくい データ全体の中央のズレ具合を捉える 信頼性の高い評価が可能 |
ズレの全体像を捉えることが難しい ズレの分布全体や、どれだけのデータがどれくらいずれているのかといった詳しい情報は分かりにくい 微分ができないため、モデルの学習過程で直接的にこの指標を最小化することはできない ズレの方向性を無視する |
