非階層的クラスタリング:データの自動分類

AIを知りたい
先生、「非階層的クラスタリング」って、どういう意味ですか?難しくてよくわからないです。

AIエンジニア
そうだね、少し難しいね。「非階層的クラスタリング」は、データの集まりをいくつかのグループに分ける方法の一つだよ。グループ分けの良し悪しを数値で表す「関数」を考えて、その関数の値が最大になるようにグループ分けしていくんだ。

AIを知りたい
グループ分けの良し悪しを数値で表すんですか?どんな風に数値で表すのですか?

AIエンジニア
例えば、同じグループ内のデータは出来るだけ似ていて、違うグループのデータは出来るだけ違っているようにグループ分けしたいよね。その「似ている」「違っている」を数値で表すことで、グループ分けの良し悪しを数値で評価できるようになるんだよ。そして、その数値が最大になるように、繰り返し計算してグループ分けを調整していくんだ。
非階層的クラスタリングとは。
『非階層的クラスタリング』という人工知能の用語について説明します。これは、いくつかのものをグループに分ける方法の一つです。まず、グループ分けの良し悪しを数値で表す計算式を決めます。次に、何度も計算を繰り返すことで、その計算式の値が最も良くなるようにグループを分けていきます。
はじめに

近年の情報化社会においては、膨大な量のデータが日々生み出されています。このデータの洪水とも呼べる状況の中で、価値ある情報を効率的に抽出することは、様々な分野で共通の課題となっています。非階層的クラスタリングは、この課題を解決する上で非常に有効な手法です。これは、データの集まりをいくつかのグループ、すなわち集団に分ける作業を自動的に行ってくれる方法です。データ同士の類似性に基づいて集団を形成するため、データの中に隠された規則性や関連性を見つけ出すことができます。
非階層的クラスタリングは、あらかじめ集団の数を指定する必要があるという特徴があります。例えば、顧客の購買情報を分析して、顧客を3つのグループに分けたい場合、あらかじめ3つの集団を作ることを指定します。そして、分析対象となる顧客一人ひとりの購買履歴、例えば購入した商品の種類や金額、購入頻度などを基にして、互いに似通った特徴を持つ顧客同士が同じ集団に属するように分類していきます。
この手法は、様々な分野で応用されています。例えば、販売促進の分野では、顧客の購買行動を分析することで、顧客層を特定し、効果的な販売戦略を立てることができます。医療の分野では、患者の症状や検査結果を基に、病気の種類を分類し、適切な治療法を選択するのに役立ちます。また、画像認識の分野では、画像に写っている物体を自動的に識別するために利用されます。例えば、大量の写真の中から、特定の人物や物体が写っている写真を自動的に探し出すことができます。このように、非階層的クラスタリングは、データ分析を通して新たな知見を獲得し、意思決定を支援するための強力な道具と言えるでしょう。
| 手法 | 概要 | 特徴 | 応用分野 | 利点 |
|---|---|---|---|---|
| 非階層的クラスタリング | データの集まりをいくつかのグループに自動的に分割する手法 | あらかじめ集団の数を指定する必要がある | 販売促進、医療、画像認識など | データの中に隠された規則性や関連性を見つけ出すことができる、新たな知見を獲得し意思決定を支援する |
手法の仕組み

非階層的クラスタリングとは、データの集まりをいくつかのグループ(かたまり)に分類する手法で、あらかじめグループの階層構造を定めないことが特徴です。この手法では、「グループ分けの良さ」を数値で表す関数、つまり評価関数を用いて、最適なグループ分けを探し出します。この評価関数は、同じグループに属するデータ同士の似ている度合いが高く、異なるグループに属するデータ同士の似ている度合いが低いほど、大きな値になるように設計されます。
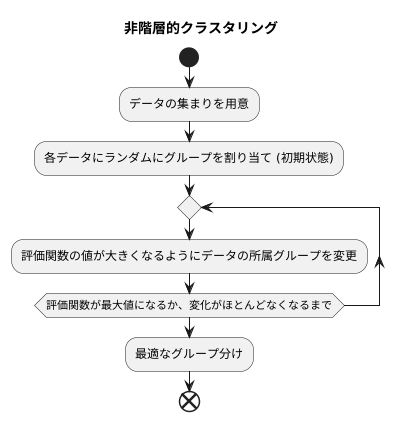
具体的な手順を見てみましょう。まず、それぞれのデータにランダムにグループを割り当てます。これは、初期状態を設定する作業です。次に、評価関数の値がより大きくなるように、データの所属するグループを繰り返し変えていきます。たとえば、あるデータを別のグループに移動させたときに、評価関数の値が大きくなる場合、その移動を実行します。このように、データの所属グループを少しずつ調整することで、評価関数の値を徐々に大きくしていきます。この繰り返し計算は、評価関数が最大値になるか、変化がほとんどなくなるまで続けられます。そして最終的に、評価関数が最大値または一定の値に落ち着いた時点で、最適なグループ分けが得られたと判断します。この手法は、データの性質に応じて様々な評価関数を用いることができ、柔軟なグループ分けを実現できることが利点です。ただし、初期状態のランダム性や評価関数の選び方によって、結果が異なる場合があるため、注意が必要です。
代表的な手法

データの集まりを似た者同士でグループ分けする手法は、大きく分けて二つの種類があります。一つは階層構造を作る方法、もう一つは階層構造を作らない方法です。ここでは、階層構造を作らない方法、つまり非階層的クラスタリングについて、代表的な手法をいくつか詳しく見ていきましょう。
まず、よく知られている手法の一つに、中心点を使う方法があります。この方法は、あらかじめいくつのグループに分けるかを決めておき、それぞれのグループの中心となる点を見つけ、データを中心点に最も近いグループに割り当てていきます。この中心点をグループの平均値で求めるのが「平均値を使う方法」です。この方法は、計算の手間が少ないため、たくさんのデータを扱う時に便利です。しかし、極端に異なる値(外れ値)が含まれていると、中心点が外れ値に引っ張られてしまい、うまくグループ分けできないことがあります。
次に、外れ値の影響を受けにくい方法として、中心点の代わりに代表点を使う方法があります。これは、データの中から代表となる点を選び、その点に最も近いデータを同じグループに割り当てる方法です。この代表点をメドイドと呼び、この方法は「メドイドを使う方法」と呼ばれています。この方法は、外れ値に左右されにくいという利点がありますが、中心点を使う方法に比べて計算に時間がかかるという欠点があります。
このように、非階層的クラスタリングには様々な手法があり、それぞれに長所と短所があります。扱うデータの特徴や分析の目的を考え、どの手法が最も適しているかを判断することが大切です。例えば、計算の速さを重視する場合は中心点を使う方法、外れ値の影響を避けたい場合は代表点を使う方法といったように、状況に応じて適切な手法を選びましょう。
| 手法 | 説明 | 長所 | 短所 |
|---|---|---|---|
| 中心点を使う方法(平均値を使う方法) | あらかじめグループ数を決め、中心点を見つけ、中心点に最も近いグループにデータを割り当てる。中心点はグループの平均値。 | 計算の手間が少ない。たくさんのデータを扱う時に便利。 | 極端に異なる値(外れ値)が含まれているとうまくグループ分けできない。 |
| 代表点を使う方法(メドイドを使う方法) | データの中から代表点(メドイド)を選び、その点に最も近いデータを同じグループに割り当てる。 | 外れ値に左右されにくい。 | 中心点を使う方法に比べて計算に時間がかかる。 |
適切なグループ数の決定

いくつかの集まりに分ける作業をする際に、いくつの集まりを作るのが良いのかを決めるのはとても大切です。集まりの数が少なすぎると、分けたいものの特徴がうまく表せません。例えば、果物をただ「甘いもの」と「甘くないもの」に分けただけでは、いちごとりんごを同じグループにしてしまうことになり、それぞれの持ち味を見逃してしまいます。反対に、集まりの数が多すぎると、今度はそれが何を意味するのか分からなくなってしまいます。果物を「赤いもの」「黄色いもの」「緑色のもの」…と細かく分けていくと、確かに色は区別できますが、味や食感などの大切な情報は見失ってしまいます。しかも、少しの違いに振り回されて、分類が不安定になることもあります。
では、ちょうど良い集まりの数を見つけるにはどうすれば良いのでしょうか?いくつかの便利な方法があります。よく使われるのが、「ひじ法」と呼ばれるやり方です。これは、集まりの数を少しずつ変えながら、それぞれの分け方の良さを数値で表し、それをグラフに描いていきます。すると、グラフの形があるところで「ひじ」のように折れ曲がることがあります。この「ひじ」の部分が、ちょうど良い集まりの数を示していると考えられています。
もう一つ、「影絵法」と呼ばれる方法もあります。これは、それぞれのものが、自分のいる集まりの中でどれくらい周りのものと似ているか、そして他の集まりとはどれくらい違っているかを数値で表します。この数値が高いほど、そのものは適切な集まりに属していると考えられます。すべてのものの数値の平均値を見て、それが最も高くなる時の集まりの数が、最適な数だと判断します。
これらの方法は、あくまでも目安です。実際に集まりに分ける際には、分けたいものの性質や、何のために分けるのかといった目的も考慮して、一番良い集まりの数を慎重に選ぶ必要があります。例えば、見た目で果物をグループ分けしたいのか、それとも味でグループ分けしたいのかによって、最適なグループ数は変わってきます。このように、状況に応じて適切な判断をすることが重要です。
| 方法 | 説明 | メリット | デメリット |
|---|---|---|---|
| ひじ法 | 集まりの数を少しずつ変えながら、それぞれの分け方の良さを数値で表し、グラフに描いた時に「ひじ」のように折れ曲がるところを探す。 | 比較的簡単に最適な集まりの数を見つけることができる。 | 数値化の指標が難しい場合がある。ひじの部分が明確でない場合もある。 |
| 影絵法 | それぞれのものが、自分のいる集まりの中でどれくらい周りのものと似ているか、そして他の集まりとはどれくらい違っているかを数値で表し、その平均値が最も高くなる集まりの数を探す。 | 集まりの質を定量的に評価できる。 | 計算コストが高い場合がある。 |
まとめ

データの集まりをいくつかのグループに分ける手法は、全体像を掴むのに役立ちます。階層構造を作らずにグループ分けする手法を非階層的クラスタリングと言い、データ同士の似ている度合いを見て自動的にグループを形成します。この手法は様々な分野で活用されており、隠れた規則性やデータ間の繋がりを見つけるために役立ちます。
非階層的クラスタリングには、いくつか種類があります。よく使われる手法の一つがk平均法です。これは、あらかじめいくつのグループに分けるかを決めておき、各データがどのグループに属するかを繰り返し計算することで、最適なグループ分けを見つけ出す手法です。計算が比較的簡単なため、大規模なデータにも適用しやすいという利点があります。しかし、外れ値の影響を受けやすいという欠点もあります。
もう一つ代表的な手法がkメドイド法です。k平均法と似ていますが、各グループの中心に選ばれるのが、必ず既存のデータの中から選ばれます。そのため、外れ値の影響を受けにくいという利点があります。ただし、k平均法に比べると計算に時間がかかるという欠点もあります。
非階層的クラスタリングを行う上で、グループ数を適切に決めることは非常に重要です。グループ数が少なすぎると、重要な情報を見落としてしまう可能性があります。逆にグループ数が多すぎると、解釈が難しくなり、実用性が低下する可能性があります。最適なグループ数を決めるためには、エルボー法やシルエット分析などの方法が使われます。エルボー法は、グループ数を変化させた際の指標の変化を見て、最適なグループ数を見つけ出す方法です。シルエット分析は、各データがどれだけ綺麗にグループに所属しているかを評価し、最適なグループ数を見つけ出す方法です。
このように、非階層的クラスタリングは、データ分析の精度を高め、より深い理解を可能にする強力な手法です。データの特性や分析の目的に合わせて適切な手法とグループ数を選ぶことが重要です。今後、データの重要性が増していく中で、非階層的クラスタリングはデータ分析に欠かせない道具として、さらに活躍の場を広げていくと考えられます。
| 手法 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| k平均法 | あらかじめグループ数を決め、各データがどのグループに属するかを繰り返し計算し、最適なグループ分けを見つけ出す。 | 計算が比較的簡単で、大規模データにも適用しやすい。 | 外れ値の影響を受けやすい。 |
| kメドイド法 | k平均法と似ているが、各グループの中心は既存のデータから選ばれる。 | 外れ値の影響を受けにくい。 | k平均法より計算に時間がかかる。 |
グループ数の決め方
| 方法 | 説明 |
|---|---|
| エルボー法 | グループ数を変化させた際の指標の変化を見て、最適なグループ数を見つけ出す。 |
| シルエット分析 | 各データがどれだけ綺麗にグループに所属しているかを評価し、最適なグループ数を見つけ出す。 |
