ROC曲線とAUCによるモデル評価

AIを知りたい
先生、『ROC曲線とAUC』って、なんか難しそうでよくわからないんですけど…簡単に説明してもらえますか?

AIエンジニア
そうだな、簡単に言うと、AIがどれだけ正しく物事を判断できるかを測るための道具の一つだよ。たとえば、ネコとイヌを見分けるAIを作ったとしよう。ROC曲線とAUCを使えば、そのAIがどれだけ正確にネコとイヌを見分けられるかを評価できるんだ。

AIを知りたい
へえ、そうなんですね。でも、具体的にどうやって測るんですか?

AIエンジニア
AIは、ネコかイヌか判断する時に、自信の度合いを持っている。その自信の度合いのしきい値をいろいろ変えて、実際に正しく判断できた割合と、間違えて判断した割合を計算してグラフにする。そのグラフがROC曲線で、グラフの下の面積がAUCだ。AUCが大きいほど、AIの判断の精度が高いと言えるんだよ。
ROC 曲線と AUCとは。
『ROC曲線とAUC』というAI用語について説明します。ROC曲線は、実際に正しいデータを正しく予測できた割合(真陽性率)と、実際は誤っているデータを誤って正と予測した割合(偽陽性率)をグラフに描いたものです。AUCは、このROC曲線の下の面積を指します。あるAIモデルの予測の厳しさを調整することで、いくつもの点をグラフに描き、それらを繋いでROC曲線を作ります。AUCの値が大きいほど、精度の高いモデルであると言えます。
ROC曲線とは

二値分類問題を扱う際には、モデルの性能を測るための方法が必要です。例えば、病気の有無や商品の購入見込みなど、二つの可能性の中からどちらかを予測する状況を想像してみてください。このような場面で活躍するのが「受信者動作特性曲線」、略してROC曲線です。ROC曲線は、グラフを用いてモデルの性能を視覚的に評価することを可能にします。
この曲線は、縦軸と横軸にそれぞれ重要な指標を配置して描かれます。縦軸には真陽性率、横軸には偽陽性率をとります。真陽性率とは、実際に陽性であるデータを正しく陽性と予測できた割合のことです。例えば、実際に病気である人を正しく病気と診断できた割合がこれにあたります。一方、偽陽性率とは、実際には陰性であるデータを誤って陽性と予測してしまった割合のことです。例えば、健康な人を誤って病気と診断してしまう割合です。
ROC曲線は、様々な閾値における真陽性率と偽陽性率の組み合わせをプロットすることで描かれます。閾値とは、陽性と陰性を分ける境目となる値のことです。この閾値を変化させることで、真陽性率と偽陽性率も変化します。理想的なモデルは、真陽性率が高く、かつ偽陽性率が低いモデルです。つまり、ROC曲線においては、左上に近いほど優れた性能を示すと言えます。
ROC曲線の下部の面積(AUC)も重要な指標です。AUCは、0から1までの値を取り、1に近いほどモデルの性能が良いことを示します。AUCが0.5の場合は、ランダムな分類と変わりません。つまり、ROC曲線とAUCを用いることで、モデルの性能を視覚的にそして数値的に評価することができるのです。
AUCとは

分類問題を扱う機械学習モデルの良し悪しを測るには様々な方法がありますが、その中で「AUC」はROC曲線の下側の面積を使ってモデルの性能を数値で表す指標です。AUCは「曲線下の面積」を意味する英語「Area Under the Curve」の頭文字を取ったものです。この数値は0から1までの間の値を取り、1に近いほどモデルの性能が良いことを示します。
もしAUCが1であれば、それは完璧なモデルと言えます。この場合、検査対象が陽性か陰性かを問わず、全て正確に予測できることを意味します。例えば、ある病気の検査で、実際に病気の人を全て病気と診断し、健康な人を全て健康と診断できるということです。
反対に、AUCが0.5の場合は、モデルの性能はランダムな予測と変わりません。これは、例えばコインを投げて表が出たら陽性、裏が出たら陰性と判断するのと同程度の精度しかないということです。さらに、AUCの値が0に近づくにつれて、モデルの性能は低下していきます。0に近いAUCは、全く予測が当たらない、むしろ真逆の結果を返すようなモデルを表しています。例えば、病気の人を全て健康、健康な人を全て病気と診断してしまうような場合です。
AUCはROC曲線全体を要約した指標であるため、様々な条件下でのモデルの性能を総合的に評価するのに役立ちます。ROC曲線は、様々な閾値における真陽性率と偽陽性率をプロットした曲線ですが、AUCはその曲線の下側の面積を見ることで、閾値の設定に依存しない、モデルの全体的な性能を把握することができるのです。
| AUC値 | モデルの性能 | 説明 |
|---|---|---|
| 1 | 完璧 | 全て正確に予測可能 |
| 0.5 | ランダム | コイン投げと同程度の精度 |
| 0に近い | 非常に低い | 真逆の結果を返す |
閾値の役割

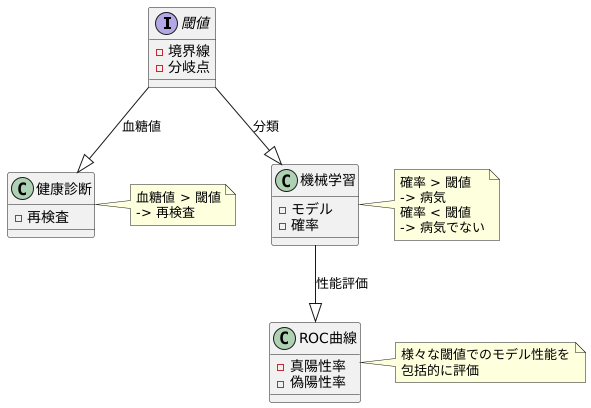
物事を仕分ける際に、境界となる線引きが必要です。この線引きの役割を果たすのが閾値です。例えば、健康診断で血糖値が一定の数値を超えると再検査が必要となります。この一定の数値が閾値にあたります。
機械学習の分類モデルでも、同じように閾値が重要な役割を担います。モデルは、様々な情報をもとに、対象がどのグループに属するかを判断します。この判断を下す際に、閾値を基準として用います。ある病気の可能性を予測するモデルを例に考えてみましょう。モデルは、様々な検査結果を入力として受け取り、病気である確率を0から1までの数値で出力します。この時、閾値を0.5に設定すると、出力値が0.5以上の場合は「病気である」、0.5未満の場合は「病気でない」と判断します。
この閾値は調整可能です。閾値を高く設定すると、病気であると判断される基準が厳しくなります。つまり、本当に病気である人を見逃す可能性は減りますが、健康な人を誤って病気と判断する可能性も高まります。逆に、閾値を低く設定すると、病気であると判断される基準が緩やかになり、健康な人を誤って病気と判断する可能性は減りますが、本当に病気である人を見逃す可能性が高まります。
ROC曲線は、この閾値を変化させた際に、モデルの性能がどう変わるかを視覚的に示すためのグラフです。具体的には、様々な閾値で、正しく「病気」と判断できた割合(真陽性率)と誤って「病気」と判断した割合(偽陽性率)を計算し、グラフ上にプロットします。閾値を変化させることで、真陽性率と偽陽性率のバランスがどう変わるかをROC曲線から読み取ることができ、目的に最適な閾値を選択することができます。
つまり、ROC曲線は、単一の閾値での評価ではなく、様々な閾値でのモデルの性能を包括的に示すことで、より深くモデルを理解するための重要な道具となるのです。
モデル比較におけるAUCの利用

異なる仕組みを持つ予測模型の良し悪しを比べるには、AUCという指標がよく使われます。たとえば、手持ちのデータを使って二つの異なる分類模型を作ったとしましょう。どちらの模型がより良い予測をするか、簡単に見分けるのは難しいかもしれません。そこで、それぞれの模型に対してROC曲線という曲線と、それから導かれるAUCという数値を計算します。
ROC曲線は、模型がどれくらい正確に物事を分類できるかを示す曲線です。そして、AUCはこの曲線の下の面積です。つまり、AUCの値が大きいほど、その模型は正確な予測ができると考えられます。AUCは0から1までの値を取り、1に近いほど良い模型と判断できます。具体的には、AUCが0.5というのは、でたらめに分類するのと変わらないことを意味します。もし0.7であれば、まずまずの分類能力を持っていると言えるでしょう。0.9以上であれば、非常に優れた分類能力を持っていると判断できます。
このように、二つの模型のAUCを比較することで、どちらの模型が優れているかを客観的に判断することができます。例えば、一方の模型のAUCが0.7で、もう一方の模型のAUCが0.8だった場合、AUCが0.8の模型の方が、より正確な予測ができると期待できます。
しかし、AUCだけで模型の良し悪しを全て判断してはいけません。AUCは全体的な分類能力を示す指標ですが、データの性質によっては注意が必要です。例えば、データの中に、ある種類のデータが非常に多く、別の種類のデータが非常に少ない場合、AUCだけでは模型の真の性能を測れないことがあります。これは、少ない種類のデータに対する予測精度が低くても、全体のAUCにはあまり影響が出ないためです。このような場合は、AUCだけでなく、他の指標も組み合わせて模型を評価する必要があります。具体的には、少ない種類のデータに対する予測精度を測る指標や、誤分類した場合の損失を考慮する指標などを用いることが考えられます。さまざまな角度から模型を評価することで、より適切な模型を選択することができます。
| AUC値 | モデルの性能 |
|---|---|
| 0.5 | ランダムな分類と同等 |
| 0.7 | まずまずの分類能力 |
| 0.9以上 | 非常に優れた分類能力 |
AUC (Area Under the ROC Curve)
- 予測モデルの良し悪しを比較するための指標。
- ROC曲線の下部の面積。
- 値が大きいほど、モデルの予測精度が高い。
- 0から1までの値を取り、1に近いほど良いモデル。
- データの性質によっては、AUCだけでは不十分な場合があり、他の指標と組み合わせて評価する必要がある。
ROC曲線とAUCの利点

分類モデルの良し悪しを判断するには、ROC曲線とAUCという方法がよく使われます。この二つを使うと、モデルの性能を視覚的に分かりやすく、そして数値で正確に評価することができます。特に、ROC曲線とAUCはデータの偏りに強いという大きな利点があります。
たとえば、病気の診断テストを考えてみましょう。ある病気にかかっている人と、そうでない人がいます。診断テストでは、病気の人を正しく「病気」と判断することを「真陽性」、病気でない人を誤って「病気」と判断することを「偽陽性」と言います。ROC曲線とAUCは、この真陽性の割合と偽陽性の割合の関係に基づいて計算されます。
現実のデータでは、病気の人とそうでない人の数は必ずしも同じではありません。病気の人が非常に少ない場合もあります。しかし、ROC曲線とAUCはこの人数の割合に影響されにくいという特徴があります。つまり、病気の人とそうでない人の割合が変わっても、ROC曲線とAUCの値は大きく変わりません。これは、データの偏りが大きい場合でも、モデルの性能を安定して評価できることを意味します。
さらに、ROC曲線を見ることで、モデルの特性をより深く理解することができます。ROC曲線は、様々な判定のしきい値における真陽性率と偽陽性率をプロットした曲線です。この曲線の形を見ることで、どのしきい値を設定するのが適切なのかを判断できます。例えば、偽陽性をなるべく少なくしたい場合は、曲線の左上部分に近いしきい値を選ぶべきです。このように、ROC曲線は実務でモデルを使う際に、最適なしきい値を決めるための重要な情報を与えてくれます。AUCはROC曲線の下部の面積であり、値が大きいほどモデルの性能が良いことを示します。簡単に性能を比較するのにも役立ちます。
| 項目 | 説明 |
|---|---|
| ROC曲線 | 様々な判定のしきい値における真陽性率と偽陽性率をプロットした曲線。モデルの特性を視覚的に理解し、最適なしきい値を判断するのに役立つ。 |
| AUC | ROC曲線の下部の面積。値が大きいほどモデルの性能が良い。モデルの性能を数値で比較するのに役立つ。 |
| 利点 | データの偏りに強い。つまり、病気の人とそうでない人の割合が変わっても、ROC曲線とAUCの値は大きく変わらない。 |
| 真陽性 | 病気の人を正しく「病気」と判断すること。 |
| 偽陽性 | 病気でない人を誤って「病気」と判断すること。 |
ROC曲線とAUCの解釈と注意点

受信者動作特性曲線(ROC曲線)と曲線下面積(AUC)は、分類モデルの性能を測る際に広く使われる指標です。特に、正解データと不正解データの割合が大きく異なる不均衡データの場合に有用です。ROC曲線は、様々な閾値における真陽性率と偽陽性率の関係を図示したもので、AUCはその曲線の下の面積を表します。AUCの値は0から1までの範囲を取り、1に近いほどモデルの性能が良いとされます。
AUCはモデルの全体的な判別能力を示す指標であり、値が高いほど、モデルが真陽性と真陰性を正しく分類する能力が高いことを示唆します。例えば、AUCが0.9に近いモデルは、ランダムに選んだ陽性サンプルと陰性サンプルを比較した場合、90%の確率で陽性サンプルの予測スコアが陰性サンプルの予測スコアよりも高くなることを意味します。
しかし、AUCが高いモデルが常に最良のモデルとは限りません。AUCはモデルの全体的な性能を示す指標であり、特定の状況における性能を反映していない可能性があります。例えば、医療診断において、病気を見逃すこと(偽陰性)のコストは、健康な人を誤って病気と診断すること(偽陽性)のコストよりもはるかに大きい場合があります。このような状況では、AUCが高いモデルであっても、偽陰性率が高ければ、適切なモデルとは言えません。また、偽陽性率が一定値以下であることが求められる場合、AUCが高いモデルがその条件を満たさない場合もあります。
したがって、ROC曲線とAUCだけを見てモデルを選択するのではなく、他の指標も併用することが重要です。例えば、適合率、再現率、F値などを考慮することで、目的や状況に合ったモデルを選択することができます。また、業務上の要件、例えば、予測にかかる計算時間や利用可能な資源なども考慮する必要があります。最終的には、AUCはあくまでもモデル選択の指針の一つであり、具体的な状況や目的を踏まえて、総合的に判断することが大切です。
| 指標 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| ROC曲線 | 様々な閾値における真陽性率と偽陽性率の関係を図示 | モデルの性能を視覚的に理解しやすい | 単一の指標で性能を要約できない |
| AUC | ROC曲線の下の面積 | モデルの全体的な判別能力を示す 0から1の値で、解釈しやすい |
|
