AIC:統計モデル選択の指針

AIを知りたい
先生、「赤池情報量基準」って、データへの当てはまりと、モデルの複雑さのバランスを見るものだっていうのは、なんとなくわかるんですけど、具体的にどういうことですか?

AIエンジニア
いい質問だね。たとえば、たくさんの点があるとして、そこに線を引いて、どれくらい点がその線に近いのかを考えることを想像してみよう。線を複雑にすれば、全ての点を通るようにすることもできるけど、それは本当に正しい線の引き方と言えるかな?

AIを知りたい
うーん、確かに、将来もっとデータが集まったら、その複雑な線から外れてしまうかもしれませんね。単純な線の方が、新しいデータにも対応できそうです。

AIエンジニア
その通り! 赤池情報量基準は、複雑すぎる線を避けて、将来のデータにもある程度対応できる、ちょうど良い複雑さの線を選ぶための基準なんだ。複雑な線は、今のデータにはよく合っても、新しいデータには合わない可能性が高い。AICは、その将来への対応も考えて、モデルの良さを評価してくれるんだよ。
赤池情報量基準とは。
人工知能の分野でよく使われる「赤池情報量基準」について説明します。この基準は、統計モデルが良いか悪いかを判断するために使われます。統計モデルを作る際には、どれくらいデータに合っているかと、モデルがどれくらい複雑かという二つの点を考える必要があります。まず、データに合っていることは大切です。しかし、あまりにデータに合わせすぎると、そのデータだけに最適化されすぎてしまい、新しいデータに対応できなくなることがあります。これは「過学習」と呼ばれます。過学習は、モデルが複雑になりすぎているときに起こりやすいです。つまり、良いモデルを作るには、データへの適合度と複雑さのバランスを取ることが重要になります。赤池情報量基準は、このバランスを測ることで、モデルの良し悪しを判断する基準となります。
はじめに

統計的な模型を作る際、その模型がどれほど現実に即しているかを測ることは非常に重要です。しかし、ただ手元の情報に合うように模型を作ると、新たな情報に対してはうまく対応できないことがあります。これは、特定の問題の答えだけを覚えた生徒が、問題文が少し変わっただけで解けなくなってしまうのと似ています。統計学では、この現象を「過学習」と呼びます。過学習は、模型が複雑になりすぎて、特定の情報のみに過剰に適応してしまうことで起こります。
この過学習を防ぎ、新しい情報にも対応できる、より汎用的な模型を作るには、情報への当てはまり具合と模型の複雑さの釣り合いを考える必要があります。赤池情報量規準(AIC)は、まさにこの釣り合いを評価するための指標です。AICは、統計的な模型の良さを評価するもので、値が小さいほど良い模型とされます。
AICは、大きく二つの要素から成り立っています。一つは、模型がどれほど情報に当てはまっているかを示す「尤度」と呼ばれる値です。尤度は、模型が観測された情報をどれほど上手く説明できるかを示す指標で、値が大きいほど、情報への当てはまりが良いことを示します。もう一つは、模型の複雑さを示す値です。一般的に、模型に含まれる変数の数が多いほど、模型は複雑になります。AICは、この二つの要素を組み合わせて計算されます。具体的には、尤度が高いほどAICは小さくなり、模型が複雑なほどAICは大きくなります。
つまり、AICを最小にするということは、情報への当てはまりが良く、かつできるだけ単純な模型を選ぶことに繋がります。このように、AICを用いることで、過学習を防ぎ、様々な状況に対応できる、より良い統計的な模型を作ることが可能になります。
| 項目 | 説明 |
|---|---|
| 過学習 | モデルが複雑になりすぎて、特定の情報に過剰に適応し、新しい情報に対応できない現象 |
| 赤池情報量規準 (AIC) | 統計モデルの良さを評価する指標。値が小さいほど良いモデル。 |
| AICの構成要素 | 尤度とモデルの複雑さ |
| 尤度 | モデルが観測された情報をどれだけうまく説明できるかを示す指標。値が大きいほど、情報への当てはまりが良い。 |
| モデルの複雑さ | モデルに含まれる変数の数など。変数が多いほど複雑になる。 |
| AICの最小化 | 情報への当てはまりが良く、かつできるだけ単純なモデルを選ぶことに繋がる。 |
モデルの複雑さとデータへの当てはまりの関係

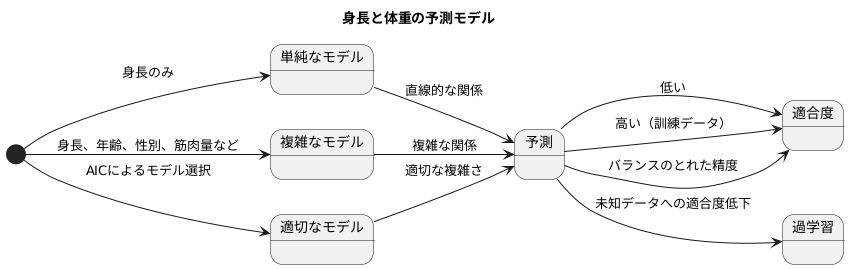
人が背が高いほど体重も重くなる傾向があるというのは、誰もが何となく知っていることです。では、実際に身長から体重を予測する数式を作るとしたら、どのようなものが考えられるでしょうか。
一番簡単な方法は、身長と体重の関係を直線で表すことです。これは単純なモデルで、計算も容易です。しかし、現実の世界では、身長と体重の関係は必ずしも直線ではありません。同じ身長の人でも、年齢や性別、運動習慣などによって体重は大きく異なるからです。
より正確に体重を予測するためには、身長だけでなく、年齢、性別、筋肉量など、様々な要素を加える必要があります。このように多くの要素を考慮したモデルは複雑なモデルと呼ばれます。複雑なモデルは、単純なモデルよりも多くの情報を扱えるため、既知のデータ(訓練データ)の点により正確に近づくことができます。まるで訓練データに合わせて自在に形を変えることができる粘土のように、複雑なモデルは訓練データの細かな変化にも対応できます。
しかし、複雑すぎるモデルには落とし穴があります。訓練データに過度に適応しすぎてしまい、未知のデータに対する予測精度が低下するという問題です。これは、まるで訓練データの形を完全に覚えてしまった粘土が、新しいデータの形にうまく対応できないようなものです。この現象を過学習と呼びます。
例えば、身長と体重の関係を複雑な曲線で表すモデルを考えてみましょう。このモデルは訓練データの点にはぴったりと合いますが、曲線が複雑すぎるため、新しいデータの身長に対応する体重を予測できない可能性があります。
つまり、モデルは複雑すぎても単純すぎても良い予測はできません。ちょうど良い複雑さのモデルを見つけることが重要であり、そのための指標の一つとしてAIC(赤池情報量基準)があります。AICは、モデルの複雑さとデータへの当てはまりのバランスを評価する指標であり、より良いモデルを選択する際に役立ちます。
赤池情報量基準(AIC)とは

統計の世界では、集めた情報をもとに、物事の関係性を見つけるために様々な計算方法(統計モデル)を使います。しかし、どの計算方法が最も適切なのかを選ぶのは難しい問題です。そこで、赤池情報量基準(AIC)という便利な道具が登場します。AICは、様々な計算方法の中から、情報に一番合った適切な計算方法を選ぶための指標です。
AICは、主に二つの要素を天秤にかけて計算されます。一つ目は、計算方法がどれくらいうまく情報を説明できるかという点です。これは「最大尤度」という数値で表され、この数値が大きいほど、計算方法が情報によく合っていることを示します。イメージとしては、パズルのピースがどれだけぴったりはまるかを表すようなものです。ピースがうまくはまればはまるほど、最大尤度は大きくなります。
二つ目は、計算方法がどれくらい複雑かという点です。計算方法の中には、たくさんの調整つまみ(パラメータ)を持つ複雑なものがあります。つまみが多いほど細かく調整できますが、情報に必要以上に合わせすぎてしまう可能性も出てきます。これは、過学習と呼ばれる現象で、新しい情報に対してうまく対応できないという問題につながります。AICでは、この複雑さを「パラメータ数」で表し、数値が大きいほど計算方法が複雑であることを示します。
AICは、これら二つの要素を組み合わせ、「-2 ×(最大対数尤度)+ 2 ×(パラメータ数)」という計算式で求めます。AICの値が小さいほど、良い計算方法だと判断できます。つまり、情報によく合っており、かつ、必要以上に複雑でない計算方法が選ばれるのです。AICを使うことで、様々な計算方法の中から最適なものを選び、より正確な予測や分析を行うことができます。
| 要素 | 説明 | 指標 | AICへの影響 |
|---|---|---|---|
| 情報への適合度 | 計算方法が情報をどれだけうまく説明できるか | 最大尤度(大きいほど良い) | AICを小さくする |
| 計算の複雑さ | 計算方法のパラメータの多さ | パラメータ数(小さいほど良い) | AICを大きくする |
AIC = -2 ×(最大対数尤度)+ 2 ×(パラメータ数)
AICが小さいほど良い計算方法
AICの使い方

情報量規準(AIC)は、統計モデルの良さを評価するための指標で、複数のモデルの中から最適なものを選ぶ際に役立ちます。AICを用いたモデル選択の方法を、具体例を交えて説明します。
まず、解析の対象となるデータに対して、複数の統計モデルを想定します。例えば、人の身長と体重の関係を調べたい場合、単純な直線モデル(体重 = a × 身長 + b)や、より複雑な曲線モデル(体重 = a × 身長² + b × 身長 + c)などを考えることができます。モデルの数や種類は、分析の目的やデータの特性に応じて適切に決定する必要があります。
次に、各モデルについてAICの値を計算します。AICは、モデルの複雑さとデータへの当てはまりの良さをバランスよく評価する指標です。複雑なモデルはデータによく当てはまりますが、将来の予測精度が低い場合があります。一方、単純なモデルは予測精度が高い場合もありますが、データの特徴を十分に捉えられない可能性があります。AICは、これらのトレードオフを考慮して、最適なモデルを選び出すために用いられます。計算方法は少し複雑ですが、多くの統計ソフトで自動的に計算できます。
そして、計算されたAICの値を比較し、最も小さい値を持つモデルを最良のモデルとして選択します。AICは相対的な指標なので、単独の値に意味はありません。複数のモデルのAICを比較することで、どのモデルがデータに最も適しているかを判断できます。例えば、直線モデルのAICが100、曲線モデルのAICが90の場合、曲線モデルの方がデータに良く当てはまっていると判断し、そちらを採用します。
ただし、AICはあくまでも統計的な指標の一つであり、モデル選択の唯一の基準ではありません。モデルの解釈のしやすさや、分析の目的との整合性なども考慮して、総合的に判断することが大切です。AICは強力なツールですが、万能ではないことを理解し、他の情報と合わせて適切に活用することが重要です。
| ステップ | 説明 | 例:身長と体重の関係 |
|---|---|---|
| モデルの想定 | データに対して複数の統計モデルを想定する。 |
|
| AICの計算 | 各モデルについてAICを計算する。AICはモデルの複雑さとデータへの当てはまりの良さを評価する。 | 各モデルのAIC値を計算(統計ソフトを用いることが多い) |
| AICの比較とモデル選択 | 計算されたAIC値を比較し、最も小さい値のモデルを選択する。 | 直線モデルAIC = 100, 曲線モデルAIC = 90 → 曲線モデルを選択 |
| 注意点 | AICは統計的な指標の一つであり、モデル選択の唯一の基準ではない。モデルの解釈のしやすさや分析目的との整合性も考慮する。 | AICだけでなく、他の情報も合わせて総合的に判断する。 |
AICの利点

情報量規準(AIC)は、統計モデルの良さの指標であり、様々な利点を備えています。まず、AICの計算は比較的容易です。複雑な計算を必要とせず、手軽に算出できるため、多様なモデルに適用し、比較検討を行うことができます。膨大な計算資源や時間を必要とするような複雑な手法と比べ、AICは手軽に利用できるため、分析作業の効率化に繋がります。
次に、AICはモデルの複雑さを適切に評価します。統計モデルは、説明変数を多くすればするほど、データへの当てはまりは良くなります。しかし、説明変数が多い複雑なモデルは、観測データの特殊な変動にも適合してしまうため、将来のデータに対する予測精度が低下する「過学習」と呼ばれる問題が発生しやすくなります。AICはモデルの複雑さを罰則項として加えることで、過学習を防ぎ、予測精度の高いモデルを選択するのに役立ちます。
また、AICは様々な種類のモデルに適用できる汎用性の高い指標です。例えば、関係性を直線で表す線形モデルだけでなく、曲線で表す非線形モデル、データの時間的な変化を捉える時系列モデルなど、様々な統計モデルにもAICを適用できます。このため、異なる種類のモデルをAICという同一の基準で比較評価することが可能になり、最適なモデルを選択する上で強力な道具となります。複数の異なるモデルを比較検討する場合、それぞれのモデルに適した評価指標を用いると、比較が難しくなります。AICは様々なモデルに適用できるため、このような問題を回避できます。
最後に、AICは統計的根拠に基づいた客観的な指標です。モデルの選択は、分析者の主観に左右されがちです。AICを用いることで、客観的な基準に基づいてモデルを選択することができ、分析結果の信頼性を高めることができます。恣意的な判断を排除し、データに基づいた客観的な評価を行うことは、科学的な分析において非常に重要です。
| AICの利点 | 説明 |
|---|---|
| 計算が容易 | 手軽に算出できるため、様々なモデルに適用し比較検討を行うことが可能。分析作業の効率化に繋がる。 |
| モデルの複雑さを適切に評価 | 複雑さを罰則項として加えることで、過学習を防ぎ、予測精度の高いモデル選択に役立つ。 |
| 汎用性が高い | 線形モデル、非線形モデル、時系列モデルなど様々な統計モデルに適用可能。異なる種類のモデルを同一の基準で比較評価できる。 |
| 客観的な指標 | 統計的根拠に基づいた客観的な指標のため、分析者の主観に左右されず、分析結果の信頼性を高めることができる。 |
AICの限界

赤池情報量規準(AIC)は、統計モデルの良さを評価し、複数のモデルの中から最適なモデルを選択するための強力な道具です。しかし、万能ではなく、いくつかの限界も存在します。AICを用いる際には、これらの限界を正しく理解し、適切に扱うことが重要です。
まず、AICはモデルが真のデータ生成過程を完全に表現することはできないという前提に立っています。その上で、真のモデルにどれだけ近いかを相対的に評価します。しかし、検討しているモデルの全てが真のモデルから大きくかけ離れている場合、AICによるモデル選択は必ずしも適切な結果をもたらさない可能性があります。例えるなら、正解から遠く離れた選択肢の中から、よりましなものを選ぼうとしているようなものです。真のモデルに近い選択肢が含まれていなければ、最適な選択はできません。
次に、AICはデータ量が十分に大きいことを前提としています。データ量が限られている場合、AICの推定精度が低下し、最適なモデルを選択できない可能性があります。これは、限られた情報から全体像を推測しようとすることの難しさに繋がります。データが少ないと、偶然のばらつきに影響されやすく、真の姿を見失ってしまう可能性が高くなります。
さらに、AICは相対的な指標であるという点も重要です。つまり、AICは複数のモデルを比較し、どのモデルが相対的に優れているかを判断するための指標であり、モデルの絶対的な良さを評価することはできません。低いAICを持つモデルが必ずしも優れたモデルであるとは限らないのです。例えば、全てのモデルがデータの説明に不十分な場合でも、AICは相対的に最も低いAICを持つモデルを選択します。
最後に、AICはモデル選択のための万能の解決策ではないことを理解する必要があります。AICは統計的モデル選択における一つの有用な道具ですが、その限界を認識し、他の指標や分析手法と組み合わせて用いることで、より適切なモデル選択を行うことができます。盲目的にAICのみに頼るのではなく、データの性質や分析の目的に合わせて柔軟にAICを活用することが重要です。
| AICの限界 | 説明 | 例え |
|---|---|---|
| 真のモデルの不在 | 真のモデルが選択肢にない場合、AICによる選択は適切でない可能性がある。 | 正解から遠い選択肢から選ぶようなもの。 |
| データ量の不足 | データ量が少ないとAICの精度が低下し、最適なモデル選択ができない可能性がある。 | 限られた情報から全体像を推測することの難しさ。 |
| 相対的な指標 | AICはモデルの絶対的な良さを評価するものではなく、相対的な比較を行う。低いAICが優れたモデルを保証するわけではない。 | 不十分なモデルの中から最もマシなものを選ぶようなもの。 |
| 万能ではない | AICは一つの道具であり、他の指標や分析手法と組み合わせて使うべき。 | – |
