k-means法:データの自動分類

AIを知りたい
先生、「k-means 法」って、どうやってグループ分けするんですか?

AIエンジニア
良い質問だね。k-means法は、まず最初にデータにランダムにグループを割り振るところから始めるんだ。そして、それぞれのグループの中心点を計算して、データがどのグループの中心点に一番近いかを調べて、グループを再編成していくんだよ。

AIを知りたい
中心点を計算して、近いグループに再編成するんですね。何回も繰り返すんですか?

AIエンジニア
そうだよ。中心点がもう動かない状態になるまで、中心点の計算とグループの再編成を繰り返すんだ。k-means法で注意が必要なのは、いくつのグループに分けるか(kの値)を人間が最初に決める必要がある点だよ。
k-means 法とは。
知能機械の言葉で「ケーミーンズ法」というものがあります。これは、似たもの同士のデータは同じ仲間と考えて、データをいくつかの集まりに分ける方法です。集まりの数は、あらかじめ人間が決めておきます。この方法は、まずデータにでたらめに仲間を割り当てます。次に、各仲間の中心を見つけます。それぞれのデータについて、一番近い中心の仲間に再び割り当てます。中心の計算と仲間の割り当てを、中心が動かなくなるまで繰り返します。仲間の数を最初に決めるのは人間なので、注意が必要です。
手法の概要

「k平均法」という手法は、たくさんのデータが集まっているとき、そのデータを自動的にいくつかのグループに分ける方法です。この手法は、データがどれだけ近いか、つまり似ているかを基準にしてグループ分けを行います。似たデータは同じグループに、そうでないデータは異なるグループに属すると考えるわけです。
具体的には、まずいくつのグループに分けるかを最初に決めます。このグループの数を「k」と呼び、「k平均法」の名前の由来となっています。例えば、kを3と決めた場合、データ全体を3つのグループに分割します。
では、どのようにグループ分けを行うのでしょうか。k平均法は、各グループの中心となるデータ(中心点)をまず適当に選びます。次に、それぞれのデータがどの中心点に一番近いかを計算し、一番近い中心点のグループに属するようにデータを割り当てます。
しかし、最初の中心点の選び方は適当なので、最適なグループ分けができるとは限りません。そこで、各グループに属するデータの位置情報を元に、中心点を再計算します。そして、再計算された中心点に基づいて、再度データの割り当てを行います。この計算と割り当てを繰り返すことで、次第に最適なグループ分けに近づいていきます。中心点の位置が変化しなくなったら、グループ分けは完了です。
k平均法は、様々な分野で活用されています。例えば、お店でお客さんが何を買ったかの記録(購買履歴)を基にしてお客さんをグループ分けしたり、写真の中の領域を分割したり、普段と異なる奇妙なデータ(異常値)を見つけたりするのに使われています。このように、たくさんのデータの中から隠れた規則性や構造を見つけるための強力な方法として、データ分析の現場で広く使われています。
計算手順

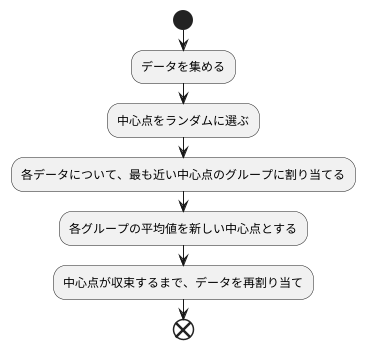
物事をいくつかの集まりに分ける手法の一つである、中心点を使った分け方の手順を見ていきましょう。この手法は、手順が分かりやすく、直感的に理解しやすいのが特徴です。まず、分けたいデータを集めます。例えば、りんごの大きさのデータや、犬の体重のデータなどです。次に、これらのデータの中から、いくつかの中心点をでたらめに選びます。中心点の数は、データの集まりをいくつのグループに分けたいかで決まります。例えば、3つのグループに分けたい場合は、3つの中心点をでたらめに選びます。これらの選ばれた中心点は、それぞれのグループの中心位置の最初の値になります。そして、集めたデータの一つ一つに対して、どの初期中心点に一番近いかを調べます。そして、一番近い中心点のグループに、そのデータを割り当てます。これで、最初のグループ分けが完了です。次に、各グループに割り当てられたデータの平均値を求めます。そして、この平均値を、新しい中心点として設定します。この新しい中心点に基づいて、もう一度全てのデータを一番近い中心点のグループに割り当て直します。このように中心点を更新し、データを再割り当てする作業を、中心点の位置がほとんど動かなくなるまで繰り返します。中心点が動かなくなると、グループ分けが安定したと考え、計算を終了します。この繰り返し計算によって、データの集まりが決められた数のグループに、うまく分けられます。中心点を使った分け方は、データの性質を捉え、似たものを集めるのに役立ちます。
グループ数の決め方
集団に分ける作業において、いくつの集団を作るかを決めるのはとても大切です。この集団の数をkとすると、kの値によって結果が大きく変わってきます。例えば、顧客をグループ分けしてそれぞれに合ったサービスを提供したい場合、kの値が小さすぎると顧客の特徴を捉えきれず、大きすぎると細かすぎて対応しきれなくなる可能性があります。
最適なkを見つける方法の一つに、ひじ型選定法というものがあります。この方法は、様々なkの値で試しに集団分けを行い、それぞれのkについて集団内のデータのばらつき具合を計算します。このばらつき具合は、各データが所属する集団の中心からの距離の平均で表すことができます。kの値を1から順に増やしていき、それぞれのkに対応するばらつき具合をグラフに描いていくと、グラフの線がひじのように折れ曲がっている点が見つかることがあります。
このひじの点が、最適なkの値の目安となります。kの値が小さいうちは、kを増やすごとにばらつき具合は大きく減少します。これは、より多くの集団に分けることで、それぞれの集団内でのデータのばらつきが小さくなるためです。しかし、ある程度kが大きくなると、ばらつき具合の減少幅は小さくなります。これは、これ以上集団を増やしても、それぞれの集団内でのデータのばらつきがあまり変わらなくなることを意味します。
ひじ型選定法では、この変化の境目となる「ひじ」の部分を最適なkとして選びます。しかし、この方法はあくまでも目安であり、必ずしも明確なひじの点が存在するとは限りません。また、データの特性や分析の目的によっては、ひじの点とは異なるkの値が適切な場合もあります。最終的には、分析を行う人がデータの内容や目的を踏まえて、最適なkの値を判断する必要があります。
長所と短所

分け合う計算の手法は、多くの利点を持っています。まず、計算の手順が比較的単純で、たくさんの情報を取り扱うことができます。膨大な量の情報を扱う現代社会において、この特徴は大きな強みです。さらに、計算結果を絵で表すことができ、結果の意味を理解しやすいことも利点の一つです。
しかし、この手法にはいくつかの弱点も存在します。計算を始める前に最初の値を設定する必要がありますが、この値によって結果が変わる可能性があります。そのため、異なる最初の値で何度も計算し、結果を比較する必要があります。これは、計算に時間がかかるという欠点につながります。
また、情報の散らばり方によっては、うまくグループ分けできない場合があります。例えば、グループの大きさや密度が大きく異なる場合や、丸くない形のグループの場合には、他のグループ分けの手法を検討する必要があるでしょう。
さらに、極端な値を持つ情報(外れ値)の影響を受けやすいという欠点もあります。外れ値はグループの中心点を大きくずらす可能性があるため、事前に外れ値を取り除くなどの準備が必要となる場合があります。これは、データの前処理に手間がかかることを意味します。このように、分け合う計算の手法は便利である一方、いくつかの注意点に気を配る必要があります。
| メリット | デメリット |
|---|---|
| 計算手順が単純 | 初期値の設定により結果が変わる |
| 大量の情報処理が可能 | 初期値を変えて何度も計算する必要があるため、時間がかかる |
| 計算結果を絵で表せるため、理解しやすい | 情報の散らばり方によっては、うまくグループ分けできない |
| 外れ値の影響を受けやすい |
適用事例

多くの分野で活用されている手法である、集団分け計算方法は、様々な場面で応用されています。
例えば、販売促進の分野では、顧客の購入履歴や顧客の特徴に基づいて集団分けすることで、顧客をいくつかの層に分類することに役立っています。それぞれの顧客層に合った商品やサービスを提供することで、顧客の満足度を高めたり、売上の増加につなげたりすることができます。例えば、若い女性向けの服を販売する会社であれば、顧客を年齢や購入履歴に基づいて「10代の流行に敏感な層」「20代の落ち着いた雰囲気を好む層」「30代のシンプルで上質なものを求める層」などに分類することで、それぞれの層に適した商品を提案し、効果的な販売戦略を立てることができます。
また、画像を扱う分野では、画像を構成する小さな点の色に基づいて集団分けすることで、画像の領域分割に活用されています。これにより、画像に写っている対象物を識別したり、背景を取り除いたりすることができます。例えば、自動運転技術では、道路標識や歩行者、他の車両などを識別するために画像認識技術が不可欠です。集団分け計算方法を用いることで、画像の中から特定の対象物を切り出し、その特徴を把握することができます。
医療の分野では、患者の症状や検査結果に基づいて集団分けすることで、病気の診断や治療方針の決定を支援しています。似た症状を持つ患者をグループ分けすることで、より正確な診断や効果的な治療法の選択が可能になります。例えば、ある特定の病気の患者をいくつかのグループに分け、それぞれのグループに特徴的な症状や検査結果を分析することで、新しい治療法の開発や既存の治療法の改善に繋げることができます。
このように、集団分け計算方法は、情報を分析する様々な場面で活用されている応用範囲の広い手法です。
| 分野 | 活用例 | 効果 |
|---|---|---|
| 販売促進 | 顧客の購入履歴や顧客の特徴に基づいて顧客を層に分類 | 顧客層に合った商品やサービスの提供による顧客満足度向上、売上増加 |
| 画像処理 | 画像を構成する小さな点の色に基づいて領域分割 | 画像に写っている対象物の識別、背景の除去、自動運転技術への応用 |
| 医療 | 患者の症状や検査結果に基づいて集団分けし、病気の診断や治療方針の決定を支援 | より正確な診断、効果的な治療法の選択、新しい治療法の開発、既存の治療法の改善 |
更なる発展

数多くの分野で活用されている「集団分け手法」の一つである「k平均法」は、データの集まりをいくつかの似た集団に分ける基本的な手法として広く知られています。しかし、現状に満足することなく、今もなお、様々な改良や発展が続けられています。
まず、この手法の弱点の一つとして、最初の集団の中心点をどこに置くかで結果が大きく変わってしまうという問題がありました。この問題を解決するために、より良い初期値の選び方を工夫する研究が盛んに行われています。例えば、データ全体を大まかに見て、中心点の候補を絞り込む方法や、何度も試行して最適な初期値を見つける方法などが提案されています。
また、k平均法は、丸い形の集団を見つけるのには得意ですが、複雑な形の集団にはうまく対応できないという課題もありました。この点を克服するために、データの分布の形に合わせて、距離の測り方を変えるなどの改良が加えられています。これにより、より複雑な形の集団にも対応できるようになり、分析の精度が向上しています。
さらに、k平均法を土台とした新しい集団分け手法も開発されています。例えば、データの密度を考慮した手法や、階層構造を持つ集団を発見する手法など、様々な手法が提案され、活用されています。これらの新しい手法は、k平均法の利点を活かしつつ、その弱点を克服することで、より幅広いデータ分析に対応できるようになっています。
このように、k平均法は、常に進化を続けている手法です。今後、データ分析技術がさらに発展していく中で、k平均法も、更なる改良や新しい手法の開発によって、より高度で複雑なデータ分析のニーズに応えていくことが期待されます。そして、データ分析においてなくてはならない手法として、これからも重要な役割を担っていくことでしょう。
| 課題 | 解決策 | 効果 |
|---|---|---|
| 初期値依存性(初期の集団の中心点の位置で結果が変わる) |
|
安定した結果を得られる |
| 複雑な形状の集団への対応不足(丸い形の集団の検出に限定) | データ分布に合わせた距離尺度の変更 | 複雑な形状の集団の検出、分析精度の向上 |
| 手法の拡張性 |
|
より幅広いデータ分析への対応 |
