k平均法:データの自動分類

AIを知りたい
先生、「k-means 法」って、どうやってデータの集まりを分けるんですか?

AIエンジニア
簡単に言うと、仲間はずれを探すように分けるんだよ。まず、いくつかグループに分けて、それぞれのグループの中心を見つける。そして、中心に近いデータを集めてグループを作り直す。これを繰り返して、中心が動かないようになったら終わりだよ。

AIを知りたい
なるほど。でも、最初のグループ分けはどうやって決めるんですか?

AIエンジニア
最初は、でたらめにグループを割り当てるんだ。そして、中心を計算して、グループを少しずつ変えていくんだよ。ただし、グループの数は人間が最初に決めておく必要がある。ここが大事なポイントだね。
k-means 法とは。
データの集まりをいくつかのグループに分ける方法の一つに、『k-平均法』というものがあります。この方法は、互いに近いデータは同じグループに属するという考え方に基づいています。まず、いくつのグループに分けるか(k個)をあらかじめ決めておきます。そして、それぞれのデータに、ランダムにグループを割り当てます。次に、各グループの中心点(重心)を計算します。それぞれのデータについて、一番近い重心を持つグループに再度割り当て直します。重心の再計算とグループの再割り当てを、重心が動かなくなるまで繰り返します。グループ数を決めるのは人間なので、適切な数を選ぶことが大切です。
手法の仕組み

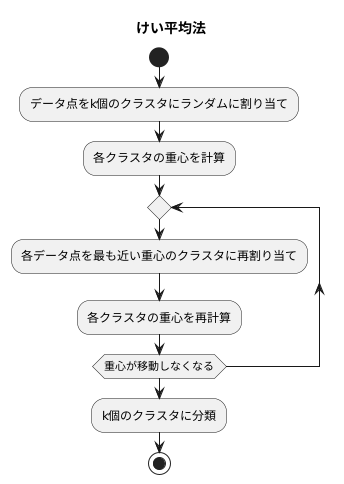
集団を自動的に仕分ける手法である「けい平均法」の仕組みについて詳しく説明します。この手法は、データ間の距離に着目し、近いデータは同じ仲間とみなす考え方です。具体的には、データをあらかじめ決めた数の集団(かたまり)に分けていきます。この集団の数を「けい」と呼びますが、「けい」の値は解析する人が最初に決めておく必要があります。
まず、それぞれのデータに、どの集団に属するかをでたらめに割り当てます。これは、いわば仮の分類です。次に、各集団の中心、すなわち重心を計算します。重心とは、その集団に属するデータの平均的な位置を示す点です。そして、それぞれのデータについて、どの集団の重心に一番近いかを調べ、一番近い重心を持つ集団にデータを再び割り当てます。この操作で、データの所属する集団が更新されます。
重心の再計算と集団の再割り当てを何度も繰り返すことで、各集団の状態は徐々に安定していきます。最終的に、重心が動かなくなったら、けい平均法の処理は終了です。この時点で、データは「けい」個の集団に分類されています。それぞれの集団には、互いに近いデータが集まっていると考えられます。
この手法は、たくさんのデータを自動的に分類するのに便利です。例えば、顧客の購買履歴を基に顧客をいくつかのグループに分けたり、商品の類似度を基に商品を分類したりする際に活用できます。また、画像認識の分野でも、画像の特徴を基に画像を分類するなどの応用が可能です。このように、けい平均法は様々な分野で活用されている、大変有用な手法です。
手法の利点

この手法には多くの利点があり、中でも分かりやすさと処理の速さが際立っています。扱う手順が簡素なため、内容を理解しやすく、実際に使うための準備も容易です。また、計算に掛かる手間が少ないため、膨大な量の情報を扱う場合でも速やかに結果を得られます。
この手法は、情報が全体的に均等に散らばっている場合、集団を効率よく作り出すことができます。それぞれの集団の中心点を繰り返し移動させることで、最適な集団分けを実現します。中心点の移動は、各集団に属する情報の平均位置を計算することで行われます。この計算は比較的簡単であり、処理速度の速さに貢献しています。
この手法は、様々な分野で情報の傾向を掴むための最初の段階として広く使われています。例えば、顧客を購買行動に基づいてグループ分けすることで、効果的な販売戦略を立てることができます。また、画像認識の分野では、画像をピクセルの色の類似性に基づいて分割することで、特定の物体を認識することができます。このように、この手法は理解しやすく、処理が速く、様々な応用が可能であるため、情報分析において非常に有用な手法と言えるでしょう。
さらに、この手法は初期値の設定に左右されるという欠点もありますが、この欠点を補うための手法もいくつか提案されています。例えば、初期値をランダムに設定するのではなく、ある程度の規則性を持たせて設定するといった工夫をすることで、より安定した結果を得ることができます。このように、様々な改良が加えられながら、この手法は現在も幅広く活用されています。
| 項目 | 内容 |
|---|---|
| 利点 | 分かりやすさ、処理の速さ |
| 手順 | 簡素で理解しやすい |
| 計算 | 手間が少なく、速やかに結果を得られる |
| 効果 | 情報が均等に散らばっている場合、効率よく集団を作り出す |
| 中心点の移動 | 各集団に属する情報の平均位置を計算 |
| 応用例 | 顧客のグループ分けによる販売戦略、画像認識における物体認識 |
| 欠点 | 初期値の設定に左右される |
| 欠点への対策 | 初期値の設定に規則性を持たせる |
手法の欠点

分けたい集団の数をあらかじめ決めておく必要があるという点が、この手法の大きな課題の一つです。集団の数を適切に決めないと、本来あるべき姿とは異なる集団分けになってしまうことがあります。例えば、本来3つの集団に分けられるべきデータを、2つの集団に無理やり分けてしまうと、それぞれの集団の中に本来属さないデータが混ざってしまい、意味のある分析結果を得ることが難しくなります。しかも、最適な集団の数を事前に知ることは、多くの場合容易ではありません。
この手法は、最初の集団分けの状態に大きく影響されるという問題点もあります。最初の集団分けが異なると、最終的な結果も変わってしまう可能性があります。同じデータを分析しているにも関わらず、最初の集団分けによって結果が変わってしまうのでは、分析の信頼性が損なわれてしまいます。安定した結果を得るためには、最初の集団分けを何度も変えて、分析を繰り返す必要があります。これは、計算の手間を増やし、時間と資源の無駄遣いにつながる可能性があります。
また、極端に異なる値、いわゆる外れ値の影響を受けやすいという欠点も無視できません。外れ値とは、他のデータから大きく離れた値のことです。例えば、多くの人の年収が300万円から500万円の範囲にある中で、年収が1億円の人が一人だけいると、この1億円というデータは外れ値となります。このような外れ値が存在すると、集団の中心が外れ値に引っ張られてしまい、本来あるべき集団の姿が歪められてしまう可能性があります。結果として、誤った分析結果を導き出してしまう危険性があります。そのため、外れ値への対策を適切に行う必要があるのです。
| 課題 | 詳細 |
|---|---|
| 集団の数の決定 | 集団の数をあらかじめ決める必要がある。 適切な数を決めないと、本来とは異なる集団分けになる可能性がある。 最適な数の事前把握は困難。 |
| 初期値依存性 | 最初の集団分けの状態に大きく影響される。 異なる初期値で結果が変わり、分析の信頼性が損なわれる。 安定した結果を得るには、初期値を変えて繰り返し分析する必要がある。 |
| 外れ値の影響 | 極端に異なる値(外れ値)の影響を受けやすい。 外れ値に集団の中心が引っ張られ、本来の集団の姿が歪む。 誤った分析結果を導き出す危険性がある。 |
クラスタ数の決定

集団の数を見極めることは、集団分けの方法を使う上でとても大切です。この集団の数をどのように決めるか、様々な方法がありますが、ここではよく使われる二つの方法を紹介します。一つ目は、肘の方法です。これは、集団の中での散らばり具合を数値で表したものを使って、集団の数を少しずつ変えながら、その数値の変化具合を見ます。数値の変化が大きいところと小さいところの境目、ちょうど肘のように曲がるところが、適切な集団の数だと考えます。
二つ目は、影絵の方法です。これは、それぞれのデータが、どのくらいしっかりと自分の集団に属しているかを数値で表し、その数値が高いほど、データが適切な集団に割り当てられていると判断します。すべてのデータの属している具合の数値の平均が高くなるように、集団の数を調整します。
肘の方法と影絵の方法は、どちらもデータの特性に合わせて適切な集団の数を見つけるための有効な手段です。肘の方法は、全体的な散らばり具合から集団の数を見積もるのに対し、影絵の方法は、個々のデータがどの程度適切に集団に属しているかを評価することで、よりきめ細やかな分析を可能にします。しかし、これらの方法だけで最適な集団の数が必ずしも決まるわけではありません。データがどのような性質を持っているのか、また、分析の目的は何なのかをしっかりと考えて、最終的な集団の数を決める必要があります。
集団の数は、分析の結果に大きな影響を与えるため、慎重に検討することが重要です。例えば、集団の数を少なく設定しすぎると、本来異なる性質のデータが同じ集団にまとめられてしまい、重要な情報を見落とす可能性があります。逆に、集団の数を多く設定しすぎると、データのばらつきが過剰に強調され、意味のある解釈が難しくなる可能性があります。そのため、様々な方法を試し、データの特性や分析の目的に合わせて最適な集団の数を選択することが重要です。
| 方法 | 概要 | 長所 | 短所 |
|---|---|---|---|
| 肘の方法 | 集団内分散を指標に、数値の変化が大きい部分と小さい部分の境目(肘)から最適な集団数を見つける。 | 全体的な散らばり具合から集団数を見積もることができる。 | データの特性によっては、肘が見えにくい場合がある。 |
| シルエット係数 | 個々のデータの所属する集団への適合度を評価し、全体平均値が最大となる集団数を探す。 | 個々のデータの所属の適切さを評価でき、きめ細かい分析が可能。 | 計算コストが高い場合がある。 |
適用事例

様々な分野で活用されている手法の一つに、集団をいくつかのまとまりに分ける方法があります。この方法は、よく知られた「仲間分けの手法」とも言われ、その適用事例は多岐に渡ります。例えば、販売促進の分野では、顧客をいくつかのグループに分けるために用いられています。顧客の過去の買い物情報や顧客の特徴を示す情報などを元に、この手法を用いることで、顧客をいくつかのグループに分類できます。こうして分けられたグループそれぞれに合った販売戦略を立てることが可能になります。
また、画像を扱う分野でも、この手法は画像の分割や特徴を取り出すために使われています。画像を構成する小さな点の色情報などをデータとしてこの手法を適用することで、画像を異なる領域に分割することが可能です。例えば、色の似ている部分を一つにまとめることで、画像中の主要な物体を見つけ出すことができます。
医療の分野でもこの手法は活用されています。例えば、患者の症状や検査結果などのデータから、似たような症状を持つ患者をグループ分けすることで、病気の診断や治療方針の決定に役立てることができます。また、健康診断の結果から、生活習慣病のリスクが高い人をグループ分けすることで、予防のための適切な指導を行うことができます。
さらに、不正を見つける分野でもこの手法は有効です。クレジットカードの利用履歴などから、通常とは異なる利用パターンを検出し、不正利用の可能性が高いものを識別することができます。このように、集団をいくつかのまとまりに分ける手法は、様々な分野で広く活用され、データ分析に基づいた意思決定を支援する重要な役割を担っています。データの特性に合わせて適切に活用することで、より効果的な分析と、それに基づく精度の高い判断が可能になります。
| 分野 | 活用例 | データ例 | 目的 |
|---|---|---|---|
| 販売促進 | 顧客のグループ分け | 購買履歴、顧客属性 | グループに最適化された販売戦略 |
| 画像処理 | 画像の分割、特徴抽出 | 画素の色情報 | 物体認識、領域分割 |
| 医療 | 患者のグループ分け | 症状、検査結果 | 診断、治療方針決定、予防指導 |
| 不正検出 | 不正利用の検出 | クレジットカード利用履歴 | 不正利用の可能性が高いものを識別 |
更なる発展

集団分けのやり方の一つとして、よく知られている方法に、ケー平均法というものがあります。これは、データの集まりをいくつかのグループに分ける方法で、それぞれのグループの中心に近いデータをまとめていくという考え方です。しかし、この方法にはいくつか弱点があります。例えば、極端に外れた値があると、グループ分けの結果に大きな影響を与えてしまうことがあります。また、最初のグループの中心をどのように決めるかによって、結果が変わってしまうこともあります。
そこで、これらの弱点を克服するために、様々な改良が加えられています。例えば、ケーメドイド法という方法では、グループの中心をデータの平均値ではなく、実際のデータの中から選びます。つまり、グループの代表となるデータを選ぶことで、外れた値の影響を受けにくくしています。この方法を使うと、極端な値に左右されずに、より正確なグループ分けができます。
また、ケー平均法プラスプラスという方法では、最初のグループの中心の決め方を工夫しています。ケー平均法では、最初のグループの中心をランダムに決めますが、ケー平均法プラスプラスでは、なるべくデータが均等に配置されるように中心を選びます。これにより、より安定した結果を得ることができるようになります。つまり、何度計算しても同じような結果が得られる可能性が高くなります。
このように、ケー平均法を改良した様々な方法が開発されています。これらの改良された方法を使うことで、ケー平均法の適用範囲はさらに広がります。例えば、従来の方法ではうまくグループ分けできなかったデータでも、これらの改良された方法を使うことで、うまくグループ分けできる可能性があります。
今後も、ケー平均法を基にした新しいグループ分けの方法が開発されていくでしょう。これらの発展により、より複雑なデータ構造にも対応できるようになり、データ分析の可能性はますます広がっていくと考えられます。例えば、人間関係のネットワークや、商品の購買履歴など、複雑なデータの分析にも活用できるようになるでしょう。これにより、今まで分からなかった隠れた関係性や法則を発見できる可能性も高まります。
| 方法 | 説明 | 長所 | 短所 |
|---|---|---|---|
| ケー平均法 | データの集まりを、それぞれのグループの中心に近いデータをまとめていく方法。 | シンプルでわかりやすい。 | 外れ値の影響を受けやすい。初期値依存性がある。 |
| ケーメドイド法 | グループの中心を実際のデータの中から選ぶ方法。 | 外れ値の影響を受けにくい。 | 計算コストが高い。 |
| ケー平均法プラスプラス | 最初のグループの中心の決め方を工夫した方法。なるべくデータが均等に配置されるように中心を選びます。 | 初期値依存性を軽減。安定した結果を得やすい。 | 計算コストがケー平均法より高い。 |
