単純パーセプトロン入門

AIを知りたい
単純パーセプトロンって、たくさんの入力から一つの結果を出すんですよね?具体的にどんな仕組みなんですか?

AIエンジニア
そうですね。複数の入力それぞれに重みづけをして、その合計値がある値を超えたら1、超えなければ0を出力する、というような仕組みです。たとえば、複数の要素から合格か不合格かを判断するようなイメージですね。

AIを知りたい
重みづけってどういうことですか?

AIエンジニア
入力の重要度を決めるようなものです。例えば、テストの点数を合計するときに、各教科の点数をそのまま足すのではなく、重要な教科の点数には大きな値をかけ、あまり重要でない教科には小さな値をかけるようなものです。重みが大きいほど、その入力の影響力が大きくなります。
単純パーセプトロンとは。
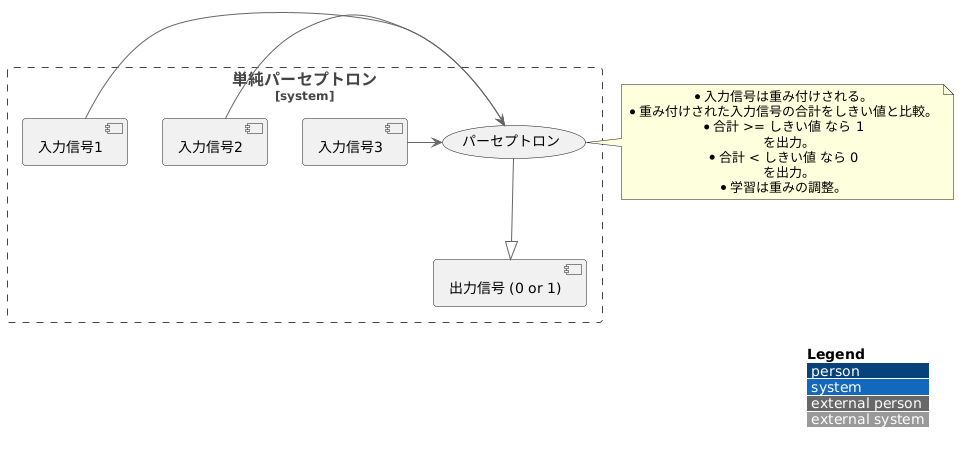
人工知能の分野でよく使われる『単純パーセプトロン』という言葉について説明します。人間の脳には神経細胞(ニューロン)がありますが、その仕組みをまねて、まずは簡単な模型を作りました。この簡単な模型のことを単純パーセプトロンといいます。この模型は、複数の入力それぞれに重み付けをして、最終的に一つの値を出力します。
単純パーセプトロンとは

単純パーセプトロンは、人間の脳の神経細胞であるニューロンの働きをまねた、基本的な計算の模型です。まるで生き物の神経細胞のように、たくさんの入力信号を受け取り、それぞれの信号に重みをつけて、最後に一つの出力信号を作ります。これは、人間の脳が様々な情報を処理して、一つの判断を下す過程とよく似ています。
具体的には、複数の入力信号がそれぞれ異なる重みを持つ接続でパーセプトロンに送られます。これらの入力信号と重みの積の合計が、パーセプトロン内部である値と比較されます。この値のことをしきい値といいます。もし、合計がしきい値よりも大きければ、パーセプトロンは「1」を出力し、小さければ「0」を出力します。この出力は、まるで脳のニューロンが発火するかしないかを表しているようです。
パーセプトロンの学習とは、この重みを調整する過程を指します。適切な重みを見つけることで、パーセプトロンは入力データに対して正しい出力を返すことができるようになります。例えば、猫と犬の画像を見分けるパーセプトロンを考えると、学習を通して「耳の形」や「鼻の形」など、猫と犬を区別する特徴に大きな重みがつけられます。
単純パーセプトロンは、線形分離可能な問題、つまり、直線や平面で綺麗に区切ることができる問題を解くことができます。しかし、線形分離不可能な問題、例えば、排他的論理和のような複雑な問題は解くことができません。それでも、単純パーセプトロンは、より複雑なニューラルネットワークの基礎となる重要な概念であり、人工知能の発展に大きく貢献しました。このシンプルな仕組みが、様々な情報を処理し、複雑な判断を下す人工知能の土台となっているのです。
仕組みを詳しく

もう少し詳しく仕組みを見ていきましょう。パーセプトロンは、複数の入り口から情報を受け取ります。それぞれの入り口には、情報の重要度を示す重みが割り当てられています。この重みは、まるで天秤の分銅のような役割を果たします。例えば、りんごの甘さを判断する場合を考えてみましょう。りんごの甘さを決める要素として、糖度と色があります。糖度は甘さに大きく影響するため、糖度という入り口には重い分銅、つまり大きな重みを付けます。一方、色は甘さへの影響が小さいため、色という入り口には軽い分銅、つまり小さな重みを付けます。
パーセプトロンは、それぞれの入り口から受け取った情報に、対応する重みを掛け合わせます。これは、それぞれの要素がどれほど甘さに貢献するかを計算しているようなものです。例えば、糖度が10で重みが5の場合、糖度による甘さへの貢献度は50と計算されます。同様に、色が赤で重みが1の場合、色による甘さへの貢献度は1となります。
次に、パーセプトロンはこれらの値を全て足し合わせます。この合計値は、りんごの甘さの総合評価を表しています。この総合評価がある基準値を超えた場合、パーセプトロンは「このりんごは甘い」と判断し、「1」を出力します。逆に、基準値を超えなかった場合は「このりんごは甘くない」と判断し、「0」を出力します。この基準値は、あらかじめ設定されたもので、しきい値と呼ばれます。
つまり、パーセプトロンは、入力された情報の重要度を重みによって調整し、総合的に判断を下しているのです。これは、人間が複数の情報を考慮して判断を下す過程と似ています。パーセプトロンは、このように単純な仕組みながらも、様々な問題を解決する能力を持っています。
学習という過程

学ぶということは、まるで種から芽が出て、ゆっくりと育っていく木のようなものです。 最初は小さな種のように、何も知らない状態から始まります。パーセプトロンという仕組みに関しても同じことが言えます。生まれたばかりのパーセプトロンは、白紙の状態です。どんな情報も持っていませんし、正しい判断もできません。
パーセプトロンが学ぶために必要なのは、経験です。具体的には、たくさんの情報と、その情報に対する正しい答えの組み合わせを繰り返し与える必要があります。例えば、猫の画像を見せて、「これは猫です」と教えます。犬の画像を見せて、「これは犬です」と教えます。この作業を何度も繰り返すことで、パーセプトロンは、猫の特徴や犬の特徴を少しずつ掴んでいきます。
この学習の過程で重要な役割を果たすのが、重み付けです。重み付けとは、それぞれの情報がどれくらい重要なのかを数値で表したものです。最初は、すべての情報に同じ重みが割り当てられています。しかし、学習が進むにつれて、重要な情報には大きな重みが、重要でない情報には小さな重みが付けられるようになります。例えば、猫を判別する際に、「耳の形」は重要な情報ですが、「背景の色」は重要でない情報です。ですから、「耳の形」には大きな重みが、「背景の色」には小さな重みが付けられるようになります。
このように、パーセプトロンは、たくさんの経験を通して、適切な重み付けを自ら学んでいきます。最初は間違った判断をすることもありますが、正しい答えを知ることで、重み付けを修正し、徐々に精度を高めていきます。まるで、何度も転びながら歩くことを覚える子供のように、パーセプトロンも試行錯誤を繰り返しながら、複雑な情報を正しく認識し、分類できるようになっていくのです。
出力の決め方

脳の神経細胞の働きをまねた仕組みであるパーセプトロンは、情報を受け取り、それを処理して結果を返す仕組みです。この結果は、どのように決まるのでしょうか。パーセプトロンは、たくさんの入り口から情報を受け取ります。それぞれの入り口には、情報の重要度を示す重みがついています。入り口から入ってきた情報は、この重みと掛け合わされます。すべての入り口からの情報を重みと掛け合わせて合計した値を、重み付き合計と呼びます。
パーセプトロンの中には、閾値と呼ばれる基準となる値が設定されています。この閾値と、先ほど計算した重み付き合計を比べます。重み付き合計が閾値より大きい場合は「1」、小さい場合は「0」を出力します。この「1」と「0」は、あらかじめ決められた意味を持ちます。
例えば、パーセプトロンを使って写真に猫がいるかどうかを判断する場合を考えてみましょう。「1」を猫がいる、「0」を猫がいないと決めておきます。パーセプトロンは、写真の情報をたくさんの入り口から受け取ります。写真の様々な特徴が、それぞれの入り口に対応しています。それぞれの入り口には重みがついており、猫の特徴と強く結びつく入り口には大きな重みが、そうでない入り口には小さな重みが設定されているとします。
パーセプトロンは、受け取った情報と重みを掛け合わせて合計し、閾値と比較します。もし、写真に猫の特徴が多く含まれていれば、重み付き合計は大きくなり、閾値を超えて「1」を出力します。つまり、「猫がいる」と判断します。逆に、猫の特徴が少なければ、重み付き合計は小さくなり、閾値を超えず「0」を出力します。つまり、「猫がいない」と判断します。このように、パーセプトロンは、二つの選択肢から一つを選ぶ問題を解くための、役に立つ道具となります。
限界と発展

単純パーセプトロンは、人間の脳の神経細胞の働きを模倣した画期的な計算モデルでした。これは、入力された情報に重みをつけて合計し、その結果があるしきい値を超えた場合にのみ出力を出すというシンプルな仕組みです。この仕組みにより、様々なパターンを認識し、分類することが可能になりました。しかし、この単純パーセプトロンには、線形分離可能な問題しか解けないという大きな限界がありました。線形分離可能とは、平面上にあるデータ群を一本の直線で綺麗に二分できることを意味します。
例えば、「排他的論理和」と呼ばれるXORという単純な論理演算を考えてみましょう。XORは、二つの入力が異なる場合にのみ「真」を返し、同じ場合には「偽」を返します。このXORの入出力の関係を平面上にプロットすると、一本の直線で二分することができません。つまり、単純パーセプトロンではXORのような問題を正しく学習することができないのです。この事実は、単純パーセプトロンの適用範囲を狭める大きな壁となりました。
しかし、研究者たちは諦めませんでした。この限界を克服するために、新たなモデルが開発されました。それが、多層パーセプトロンです。多層パーセプトロンは、入力層と出力層の間に隠れ層と呼ばれる層を複数挿入することで、より複雑な表現が可能になりました。隠れ層を追加することで、非線形な問題も解けるようになり、XORのような論理演算も学習できるようになりました。さらに、多層パーセプトロンをさらに発展させた、より複雑な構造を持つニューラルネットワークも登場しました。
単純パーセプトロンは、それ自体が万能ではありませんでしたが、これらの高度な技術の礎となりました。単純パーセプトロンの限界を認識し、それを乗り越えようとする努力が、人工知能の発展を大きく前進させたのです。現代の深層学習技術も、この単純パーセプトロンの概念を拡張したものであり、画像認識や自然言語処理など、様々な分野で目覚ましい成果を上げています。単純パーセプトロンの影響力は計り知れず、今後も人工知能の発展に貢献していくことでしょう。
| モデル | 説明 | 限界 | 解決策 |
|---|---|---|---|
| 単純パーセプトロン | 入力に重みをつけて合計し、しきい値を超えたら出力 | 線形分離可能な問題しか解けない (例: XORを学習できない) | 多層パーセプトロン |
| 多層パーセプトロン | 入力層と出力層の間に隠れ層を挿入 | – | – |
まとめとして

単純パーセプトロンは、人間の脳の神経細胞の働きを模倣した、人工知能の最も基本的な仕組みの一つです。複数の入力信号を受け取り、それぞれの信号に特定の重みをかけて足し合わせ、その合計値がある閾値を超えた場合にのみ信号を出力する、という単純な仕組みです。まるで、複数の情報源からの意見を聞き、それぞれの意見の重要度を考慮して最終的な判断を下す人間の思考過程のようです。
学習の過程では、パーセプトロンは入力データと正解データの組み合わせから、それぞれの入力信号に対する適切な重みを自動的に調整していきます。これは、過去の経験から学習し、より正確な判断を下せるように成長していく人間の学習過程と似ています。具体的には、出力結果が正解と異なる場合、重みを調整することで、次回同じ入力を受けた際に正解を出力できるように修正します。この学習プロセスを繰り返すことで、パーセプトロンは次第に精度を高めていきます。
単純パーセプトロンは線形分離可能な問題、つまり、直線や平面で綺麗に分類できる問題しか解くことができないという制限があります。これは、複雑な現実世界の問題を解決するには不十分な場合が多いです。しかし、この単純なモデルが、より複雑で高性能な人工知能技術の基礎となっています。例えば、複数のパーセプトロンを層状に積み重ねた多層パーセプトロンは、より複雑な問題を解決することができます。
単純パーセプトロンを理解することは、人工知能の仕組みを理解する上で非常に重要です。現代の高度な人工知能技術も、この単純なモデルの考え方を発展させたものと言えます。複雑なシステムも、基本的な要素の組み合わせから成り立っていることを理解することで、人工知能の全体像をより深く理解することができます。単純パーセプトロンは、まさに人工知能の出発点であり、その重要性を改めて認識する必要があります。
