機械学習における誤差関数

AIを知りたい
先生、「誤差関数」って、よく聞くんですけど、どんなものか教えてもらえますか?

AIエンジニア
いいかい? 機械学習では、コンピュータにたくさんのデータを見せて、そこからパターンを学ばせるんだ。そのとき、コンピュータの予測と本当の答えとの違いを測るものさしのようなものが「誤差関数」なんだよ。

AIを知りたい
ものさし、ですか?

AIエンジニア
そう。このものさしの値が小さいほど、コンピュータの予測が正確だということになる。だから、学習の目標はこの誤差関数の値をできるだけ小さくすることなんだ。値が小さくなるように、コンピュータは自分の予測の仕方を少しずつ変えていくんだよ。
誤差関数とは。
人工知能の話でよく出てくる「誤差関数」について説明します。機械学習では、誤差関数は損失関数とも呼ばれます。これは、作った模型が予想した値と、本当の値との違い具合を表す関数です。学習を進めていく際には、この誤差関数の値がなるべく小さくなるように、模型の細かい部分を少しずつ変えていきます。そうすることで、より正確な模型を作ることができるのです。
誤差関数の役割

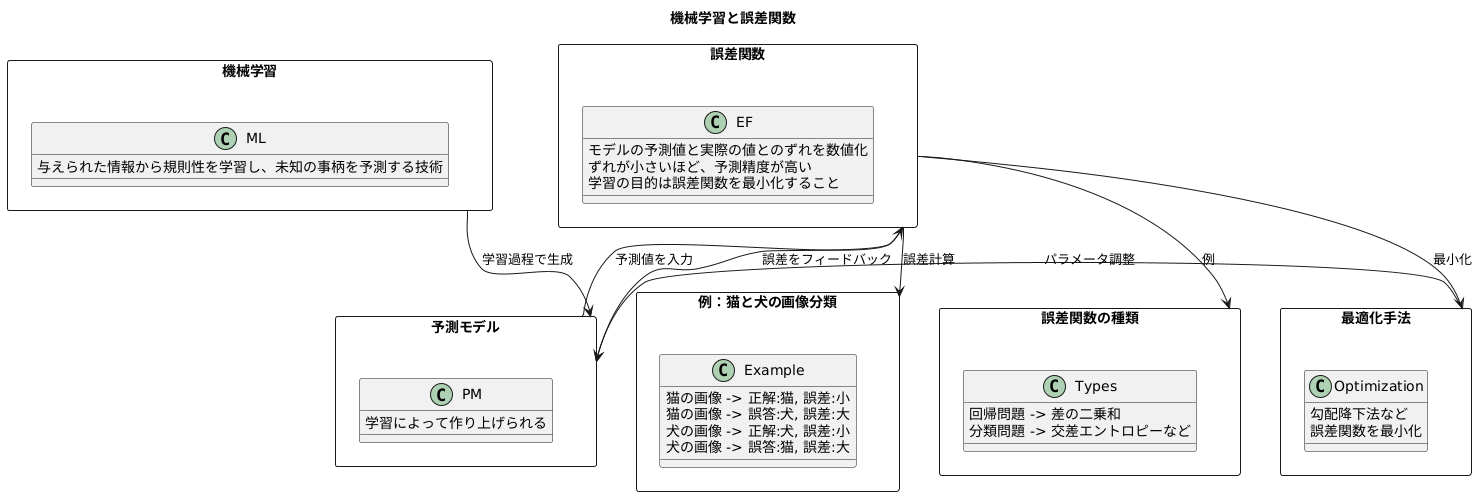
機械学習は、まるで人間の学習のように、与えられた情報から規則性を、それを元に未知の事柄について予測する技術です。この学習の過程で、作り上げた予測モデルがどれほど正確なのかを評価する必要があります。その評価の尺度となるのが誤差関数です。
誤差関数は、モデルが予測した値と、実際の正しい値との間のずれを数値で表すものです。このずれが小さければ小さいほど、モデルの予測精度が高いと判断できます。学習の目的は、この誤差関数の値を可能な限り小さくすること、つまりモデルの予測と真実の値との間のずれを縮めることなのです。
例として、猫と犬の画像を見分けるモデルを学習させる場面を考えてみましょう。このモデルに猫の画像を見せて「猫」と正しく判断できれば誤差は小さく、逆に犬と誤って判断すれば誤差は大きくなります。犬の画像を見せた場合も同様です。誤差関数は、これらの誤判断の数を基に計算されます。学習を進める中で、誤差関数の値が小さくなるようにモデルを調整することで、猫と犬の画像をより正確に見分けられるモデルへと成長させていくのです。
誤差関数の種類は様々で、扱うデータの種類やモデルの特性に合わせて適切なものを選択する必要があります。例えば、回帰問題では予測値と実測値の差の二乗和を誤差関数として用いることが一般的です。一方、分類問題では、予測の確信度を確率で表し、その確率に基づいて誤差を計算する交差エントロピーなどがよく用いられます。適切な誤差関数の選択は、モデルの学習効率と最終的な性能に大きく影響します。そして、誤差関数を最小化するために、様々な最適化手法が用いられます。これらの手法は、勾配降下法を基本としており、誤差関数の値が小さくなる方向へモデルのパラメータを調整していきます。
さまざまな誤差関数

機械学習では、モデルの予測と実際の値との間のずれを測るために誤差関数が使われます。このずれを小さくするようにモデルを調整していくことで、より精度の高い予測ができるようになります。誤差関数の種類は様々で、扱う問題の種類やデータの特性に合わせて適切なものを選ばなければなりません。代表的な誤差関数として、平均二乗誤差と交差エントロピー誤差について説明します。
平均二乗誤差は、主に数値を予測する回帰問題で使われます。例えば、家の価格や気温など、連続的な値を予測する際に用いられます。この誤差関数は、予測値と実際の値の差を二乗したものの平均を計算します。二乗することで、大きなずれはより大きな値となり、小さなずれは小さな値となります。例えば、家の価格を予測するモデルで、実際の価格が1億円、予測価格が9千万円だった場合、ずれは1千万円で、これを二乗した値が誤差の一部となります。複数のデータに対してこの計算を行い、平均することで全体の誤差を求めます。
一方、交差エントロピー誤差は、主に分類問題で使われます。例えば、画像に写っているものが猫か犬か、あるいは手書きの数字が何なのかを判別するような場合です。この誤差関数は、予測された確率分布と実際の確率分布との差を測ります。例えば、猫の画像をモデルに入力したとき、モデルは猫である確率0.8、犬である確率0.2と予測したとします。もし、画像が実際に猫であった場合、猫である確率が高いほど誤差は小さくなり、逆に犬である確率が高いほど誤差は大きくなります。複数のクラスがある場合、それぞれのクラスに対する予測確率と実際の確率から誤差を計算し、その合計を全体の誤差とします。このように、平均二乗誤差と交差エントロピー誤差はそれぞれ異なる場面で使われ、計算方法も異なります。適切な誤差関数を選ぶことで、モデルの学習効率や予測精度を向上させることができます。
| 誤差関数 | 説明 | 使用場面 | 計算方法 |
|---|---|---|---|
| 平均二乗誤差 | 予測値と実際の値の差を二乗したものの平均を計算 | 数値を予測する回帰問題(例: 家の価格、気温) | (予測値 – 実数値)^2 の平均 |
| 交差エントロピー誤差 | 予測された確率分布と実際の確率分布との差を測る | 分類問題(例: 画像認識、手書き数字認識) | 各クラスの予測確率と実際確率から誤差を計算し、合計 |
誤差関数の最小化

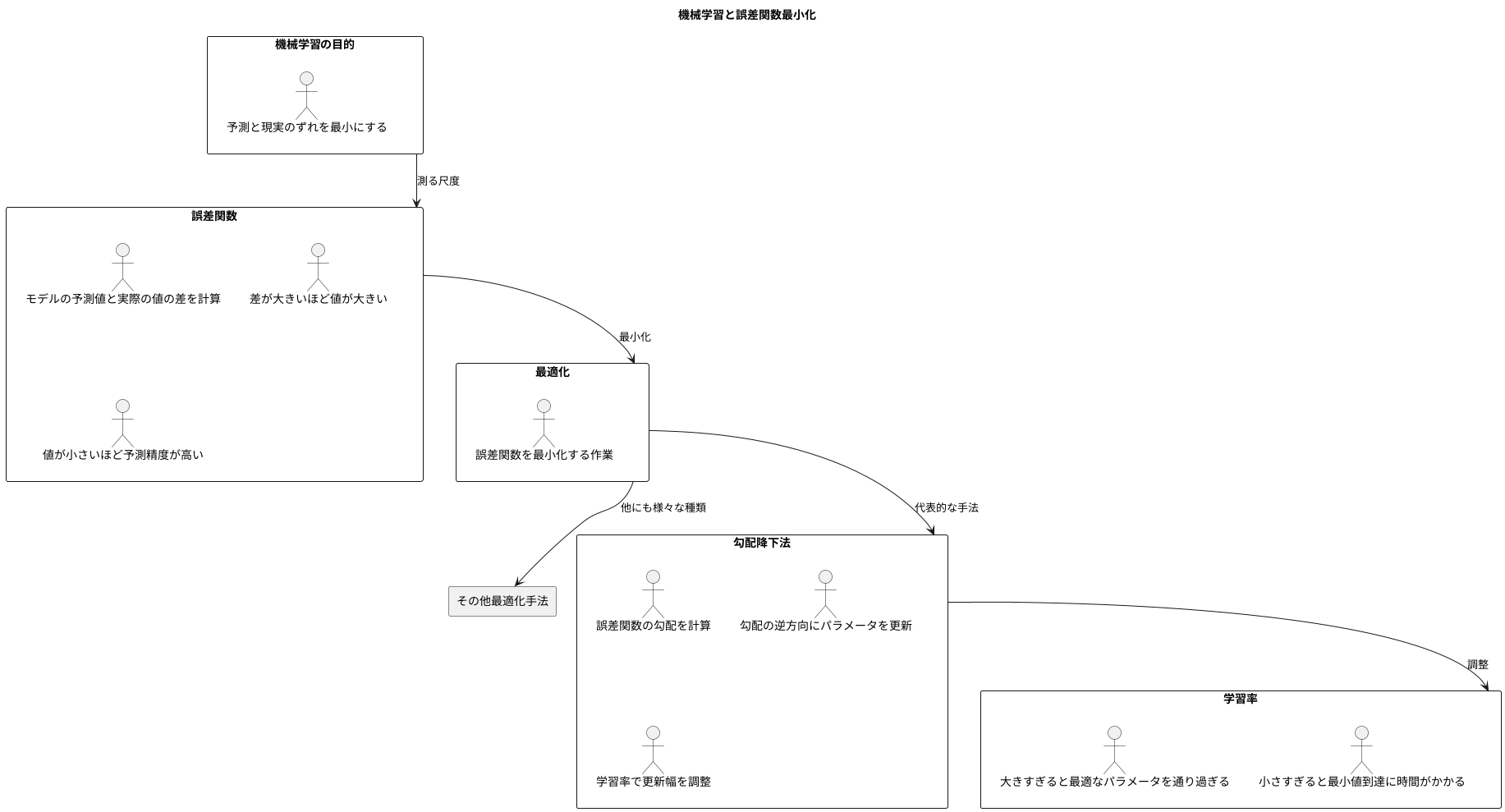
機械学習の目的は、予測と現実のずれを最小にすることです。このずれを測る尺度となるのが誤差関数です。誤差関数は、モデルの予測値と実際の値の差を計算し、その差が大きいほど値が大きくなります。つまり、誤差関数の値が小さいほど、モデルの予測精度が高いと言えます。機械学習では、この誤差関数を最小にするモデルのパラメータ、つまりモデルの挙動を調整する数値を見つけ出すことが重要になります。
この誤差関数を最小化する作業は、最適化と呼ばれます。最適化を行うための代表的な手法の一つに、勾配降下法があります。勾配降下法は、山の斜面を下るように、徐々に谷底を目指すイメージです。山全体が誤差関数だとすると、谷底は誤差関数が最小となる点です。勾配降下法では、現在の地点から少しだけ低い方向へ移動することを繰り返すことで、最終的に谷底、つまり誤差関数の最小値にたどり着きます。
具体的には、勾配降下法は誤差関数の勾配を計算します。勾配とは、関数の値が最も急激に減少する方向を示すものです。この勾配の逆方向にパラメータを少しずつ更新していくことで、誤差関数の値を減少させていきます。このパラメータの更新幅は学習率と呼ばれる値で調整されます。学習率が大きすぎると、最適なパラメータを通り過ぎてしまう可能性があり、小さすぎると、最小値に到達するまでに時間がかかってしまいます。
最適化の手法は勾配降下法以外にも様々な種類が存在し、問題の性質やデータ量、計算資源などを考慮して適切な手法を選択する必要があります。最適なパラメータを見つけることで、モデルの予測精度は向上し、より精度の高い予測を行うことができるようになります。
過学習への対処

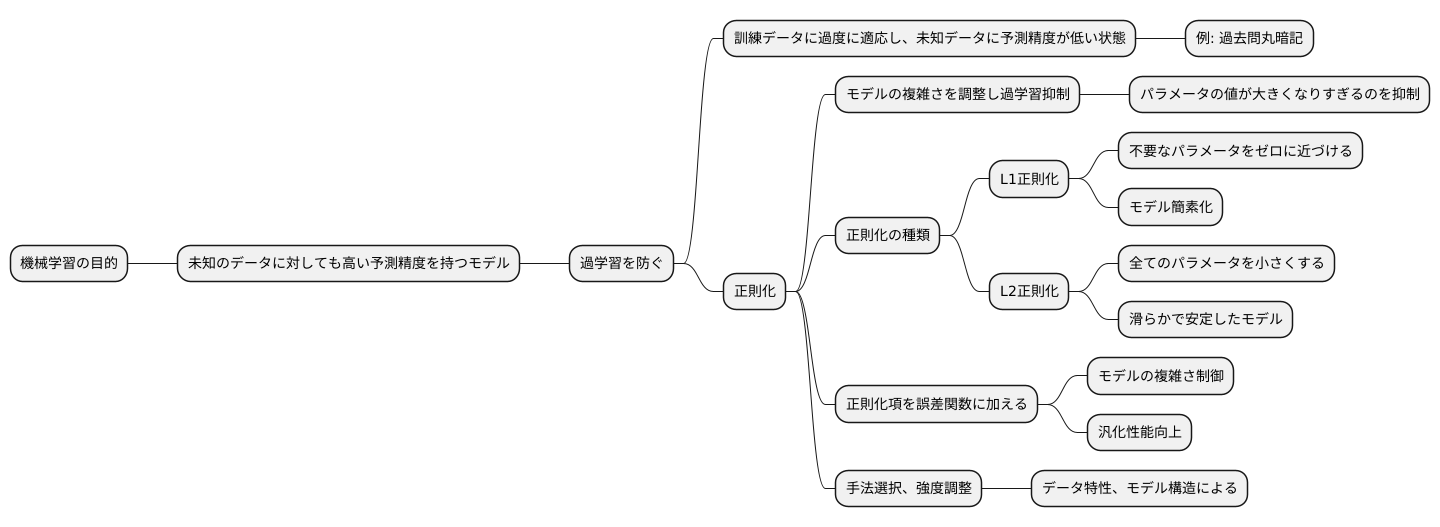
機械学習の目的は、未知のデータに対しても高い予測精度を持つモデルを構築することです。しかし、ただ単に訓練データの誤差を最小化するだけでは、必ずしも良いモデルが得られるとは限りません。訓練データに過度に適応し、未知のデータに対しては予測精度が低い状態、つまり過学習が起こる可能性があるからです。
過学習は、モデルが訓練データの個別の特徴やノイズまで学習してしまうことで発生します。例えるなら、試験対策として過去問を丸暗記するようなものです。過去問と同じ問題が出れば満点を取れますが、少しでも問題が変わると対応できません。
この過学習を防ぐための有効な手段の一つが正則化です。正則化とは、モデルの複雑さを調整することで、過学習を抑制する手法です。モデルが複雑になりすぎると、訓練データの些細な変化にも過剰に反応してしまいます。正則化は、これを防ぐためにモデルのパラメータの値が大きくなりすぎるのを抑制します。
正則化にはいくつかの種類があり、よく使われるものとしてL1正則化とL2正則化が挙げられます。L1正則化は、不要なパラメータをゼロに近づける効果があり、モデルを簡素化するのに役立ちます。一方、L2正則化は、全てのパラメータを小さくするように働き、滑らかで安定したモデルを生成する傾向があります。これらの正則化項を誤差関数に加えることで、モデルの複雑さを制御し、汎化性能を向上させることができます。
どの正則化手法を用いるかは、データの特性やモデルの構造によって異なります。適切な正則化手法を選択し、その強さを調整することで、訓練データだけでなく、未知のデータに対しても高い予測精度を持つ、より汎用的なモデルを構築することが可能になります。
誤差関数の評価

機械学習のモデルを作る際、その良し悪しを測ることはとても大切です。この良し悪しを測る方法の一つとして、誤差関数というものがあります。誤差関数は、モデルの予測と実際の値との違いを数値化したものですが、誤差関数だけを見てモデルの性能を判断するのは、少し早計と言えるでしょう。他の様々な尺度も合わせて見ていく必要があります。
例えば、写真を見てそれが猫か犬かを判断するような問題を想像してみてください。この場合、全体の予測のうち、どれだけの割合で正しく猫や犬を判別できたかを示す正解率という尺度があります。正解率が高いほど、モデルの性能が良いと言えるでしょう。しかし、正解率だけでは不十分な場合があります。例えば、猫の写真が1枚だけで、犬の写真が99枚あるような状況を考えてみましょう。もしモデルが全ての写真を犬と予測したとすると、正解率は99%となります。しかし、これは猫を全く判別できていないため、良いモデルとは言えません。
そこで、適合率と再現率という尺度も重要になります。適合率は、犬と予測した写真のうち、実際に犬である写真の割合を表します。一方、再現率は、実際に犬である写真のうち、犬と予測できた写真の割合を表します。先ほどの例では、適合率は99%ですが、猫の再現率は0%となります。これらの値を見ることで、モデルの偏りを把握できます。
さらに、適合率と再現率を組み合わせたF値という尺度もよく使われます。F値は、適合率と再現率のバランスを考慮した値で、どちらか一方だけが極端に高い場合に低い値となります。このように、誤差関数だけでなく、正解率、適合率、再現率、F値など、複数の尺度を組み合わせてモデルを評価することで、より正確にモデルの性能を把握することができます。そして、その結果をもとに、モデルをさらに改良していくことが可能となります。誤差関数はモデル学習の道標となる重要な要素ですが、最終的なモデルの評価は多角的に行う必要があることを覚えておきましょう。
| 尺度 | 説明 | 例 |
|---|---|---|
| 誤差関数 | モデルの予測と実際の値との違いを数値化したもの | – |
| 正解率 | 全体の予測のうち、正しく判別できた割合 | 猫1枚、犬99枚で全て犬と予測した場合、99% |
| 適合率 | 犬と予測した写真のうち、実際に犬である写真の割合 | 猫1枚、犬99枚で全て犬と予測した場合、99% |
| 再現率 | 実際に犬である写真のうち、犬と予測できた写真の割合 | 猫1枚、犬99枚で全て犬と予測した場合、犬は100%、猫は0% |
| F値 | 適合率と再現率のバランスを考慮した値 | – |
