交差エントロピー:機械学習の要

AIを知りたい
先生、「交差エントロピー」ってよく聞くんですけど、何なのかイマイチ分かりません。教えてもらえますか?

AIエンジニア
そうだね。「交差エントロピー」は、AIがどれだけうまく学習できているかを測るためのものだよ。 例えば、猫の絵を見て「猫」と答えるべきところで、「犬」と答えてしまったら、間違いだよね?その間違いの大きさを測るのが「交差エントロピー」なんだ。

AIを知りたい
なるほど。間違いの大きさですか。でも、単に「正解か不正解か」を見るだけじゃダメなんですか?

AIエンジニア
正解/不正解だけでは、どのくらい間違っているかがわからないんだ。「犬」と答えたのと「ライオン」と答えたのでは、間違いの程度が違うよね?「交差エントロピー」を使うと、その違いを数値で表すことができる。そして、その数値が小さくなるようにAIを学習させていくんだよ。
交差エントロピーとは。
人工知能の分野でよく使われる言葉に「交差エントロピー」があります。これは、誤差の大きさを測る関数の中で、最もよく使われているもののひとつです。この交差エントロピーは、正解の確率の分布と、機械が推定した確率の分布を比べて、その違いを測るものです。具体的には、正解の確率の値と、推定された確率の値の対数を取り、それらを掛け合わせて、最後に全部足し合わせます。そして、その符号を反転させたものが交差エントロピーの値になります。この値が小さいほど、推定した確率分布が正解に近いことを意味します。他の誤差関数と同様に、この交差エントロピーも、値が小さくなるように調整することで、人工知能の性能を向上させます。
交差エントロピーとは

機械学習、とりわけ分類問題において、予測の正確さを測る物差しとして、交差エントロピーは欠かせないものとなっています。交差エントロピーとは、真の確率分布と、機械学習モデルが予測した確率分布との間の隔たりを測る尺度です。この値が小さければ小さいほど、予測の正確さが高いことを示します。
具体例を挙げると、画像認識で、ある写真に写っているのが猫である確率をモデルが予測する場合を考えてみましょう。この写真の正しいラベル(猫である)と、モデルが予測した値(猫である確率)を比較することで、モデルの性能を評価できます。この評価に用いられるのが交差エントロピーです。猫である確率が90%と予測し、実際に猫だった場合、交差エントロピーは低い値になります。逆に、猫である確率を10%と予測した場合、交差エントロピーは高い値になり、予測の正確さが低いことを示します。
交差エントロピーは、情報理論という考え方に基づいています。情報理論とは、情報の価値や量を数学的に扱う学問です。交差エントロピーは、真の分布と予測分布がどれほど違うかを、情報量の視点から評価します。つまり、予測が真の分布から離れているほど、交差エントロピーの値は大きくなり、予測が真の分布に近いほど、値は小さくなります。
この性質を利用して、機械学習モデルの学習過程では、交差エントロピーを最小にするように、様々な調整を行います。これにより、モデルの予測精度を高めることができます。交差エントロピーは単なる数値ではなく、モデルの改善に役立つ重要な指標なのです。
| 用語 | 説明 |
|---|---|
| 交差エントロピー | 真の確率分布とモデルの予測分布の間の差を測る尺度。値が小さいほど予測精度が高い。 |
| 情報理論 | 情報の価値や量を数学的に扱う学問。交差エントロピーはこの考え方に基づく。 |
| 機械学習モデルの学習 | 交差エントロピーを最小にするように調整を行い、予測精度を高める。 |
| 予測精度 | 交差エントロピーが低いほど、予測精度が高い。 |
| 例:画像認識 | 猫の画像を「猫」と予測する確率が高いほど、交差エントロピーは低く、予測精度が高い。 |
計算方法

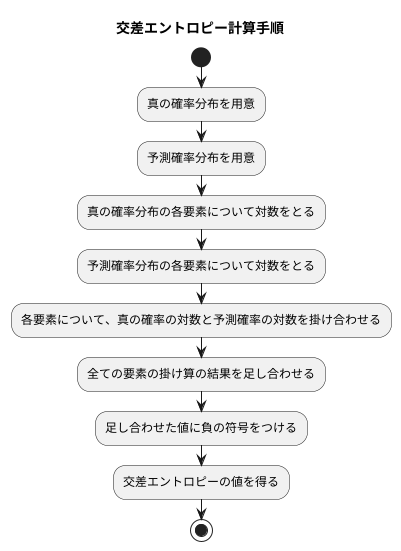
計算の手順を順を追って説明します。まず、計算に使うものとして真の確率分布と予測確率分布の二つがあります。真の確率分布とは、例えば画像に猫が写っていれば1、写っていなければ0といった具合に、正しい答えがどの程度確実なのかを表すものです。一方、予測確率分布とは、機械学習のモデルが各々の答えの可能性をどれくらいだと予測したかを表すものです。
交差エントロピーはこの二つの分布を使って計算します。具体的な手順としては、まず真の確率と予測確率のそれぞれについて対数をとります。次に、真の確率の対数と予測確率の対数の掛け算を行います。これを全ての答えの候補について行い、その結果を全て足し合わせます。最後に、足し合わせたものに負の符号を付ければ、交差エントロピーの値が得られます。
この計算によって、真の分布と予測分布がどれくらい離れているかを数値で測ることができます。計算結果は常に0かそれより大きな値になり、0に近いほど予測の正確さが高いことを示します。もし予測分布が真の分布と完全に一致していれば、交差エントロピーは0になります。つまり、交差エントロピーの値が小さいほど、モデルの予測が正しい答えに近いと言えるのです。
例として、画像に猫が写っているかいないかを判定するモデルを考えてみましょう。真の答えが「猫がいる」で、モデルが「猫がいる」と予測する確率を0.9、「猫がいない」と予測する確率を0.1とした場合、交差エントロピーはどのように計算されるでしょうか。真の確率分布は「猫がいる」が1、「猫がいない」が0です。これらの値と予測確率を使って計算を行うと、交差エントロピーの値が求まります。この値が小さければ小さいほど、モデルが正しく「猫がいる」と判断できていると言えるわけです。
最適化との関連

機械学習の模型を作る際には、その模型の良し悪しを測るための物差しが必要です。この物差しの一つに交差エントロピーというものがあります。交差エントロピーは、模型が作った答えと本当の答えとの間の違いを測る尺度で、この値が小さいほど、模型の答えが真実に近いことを示します。
模型の学習とは、この交差エントロピーをなるべく小さくするように、模型の中の部品(パラメータと呼ばれる)を調整していく作業です。ちょうど、職人が作品を少しずつ修正して完成度を高めていくように、機械学習の模型も、パラメータを調整することでより良い予測をするように学習していきます。
この調整作業を助けるのが最適化手法と呼ばれるものです。最適化手法は、交差エントロピーがどのくらい変化するかを調べながら、パラメータを効率的に調整する方法を提供します。具体的には、勾配と呼ばれる値を計算します。勾配とは、パラメータを少しだけ変えたときに、交差エントロピーがどれくらい変化するかを示す値です。勾配が大きい方向へパラメータを動かせば、交差エントロピーを大きく減らすことができ、逆に勾配が小さい方向では、交差エントロピーの変化も小さいです。
最適化手法は、この勾配情報を巧みに利用して、交差エントロピーを最小にする方向へパラメータを調整していきます。まるで山の斜面を下るように、勾配の急な方向へ進むことで、より速く谷底(最小値)にたどり着くことができます。
このように、最適化手法は、交差エントロピーと勾配という情報を手がかりに、模型のパラメータを調整し、模型が学習データからより正確な予測をできるように助ける重要な役割を果たしています。このおかげで、機械学習の模型は、与えられたデータから複雑なパターンを学習し、様々な問題を解決することができるようになります。
他の誤差関数との比較

機械学習では、目的とする問題の種類やデータの特性に合わせて、様々な誤差関数を使い分けます。誤差関数は、予測値と真の値との差を測る尺度であり、この差を小さくするように学習を進めていきます。
よく知られている誤差関数のひとつに、平均二乗誤差があります。これは、主に回帰問題で使用されます。回帰問題とは、連続的な数値を予測する問題で、例えば、気温の予測や株価の予測などが挙げられます。平均二乗誤差は、予測値と真の値の差を二乗し、その平均を計算することで求められます。このため、大きなずれを持つ予測に対しては、より大きなペナルティが課されることになります。
一方、分類問題では、交差エントロピー誤差関数がよく用いられます。分類問題とは、データがどの種類に属するかを予測する問題で、例えば、画像認識や迷惑メールの判別などが挙げられます。交差エントロピーは、予測された確率分布と真の確率分布との間の違いを表す尺度です。真の値と予測値が近いほど、交差エントロピーの値は小さくなります。
交差エントロピーには、計算上の利点があります。交差エントロピーの式には対数関数が含まれており、この対数関数の性質により、勾配の計算が容易になります。勾配とは、誤差関数を最小化する方向を示すものであり、学習アルゴリズムはこの勾配に基づいてモデルのパラメータを調整します。勾配計算が容易であるということは、学習の速度を向上させることに繋がります。
このように、平均二乗誤差と交差エントロピーは、それぞれ異なる問題に適した誤差関数です。平均二乗誤差は連続値の予測に適しており、交差エントロピーは分類問題に適しています。適切な誤差関数を選ぶことで、モデルの学習効率を高め、より精度の高い予測を行うことができます。それぞれの誤差関数の特性を理解し、問題に合わせて適切に選択することが重要です。
| 誤差関数 | 問題の種類 | 説明 | 計算上の利点 |
|---|---|---|---|
| 平均二乗誤差 | 回帰問題 (連続値予測, 例: 気温予測, 株価予測) | 予測値と真の値の差を二乗し、その平均を計算。大きなずれを持つ予測に大きなペナルティ。 | – |
| 交差エントロピー誤差関数 | 分類問題 (種類判別, 例: 画像認識, 迷惑メール判別) | 予測された確率分布と真の確率分布との間の違いを表す尺度。真の値と予測値が近いほど値は小さい。 | 対数関数により勾配の計算が容易になり、学習速度向上 |
具体的な使用例

交差エントロピーは、機械学習の様々な場面で活用されている、大切な指標の一つです。これは、ある事象の予測と実際の結果がどれだけ離れているかを示す尺度であり、この尺度を用いて、機械学習モデルの学習を進めていきます。
画像を認識するタスクを考えてみましょう。例えば、猫や犬、鳥などの動物の画像をコンピュータに見せて、それがどの動物なのかを自動的に判断させる場合を想像してみてください。この時、コンピュータは、それぞれの画像がどの動物であるかについて、確率を計算します。例えば、ある画像について「80%の確率で猫、15%の確率で犬、5%の確率で鳥」といった具合です。そして、交差エントロピーは、このコンピュータの予測と、実際の正解(例えば、その画像が実際に猫である)との間のずれを測るために使われます。ずれが小さければ小さいほど、コンピュータの予測精度は高いと言えます。
自然言語処理の分野でも、交差エントロピーは重要な役割を果たします。例えば、日本語の文章を英語に翻訳する機械翻訳システムを開発する場合を考えてみましょう。このシステムは、入力された日本語の文章に対して、様々な英語の訳を生成し、それぞれの訳がどれくらい適切かを確率で表します。そして、交差エントロピーを用いて、生成された英語の訳と、実際に正しい英語の訳との間のずれを計算し、システムの性能を評価します。このずれが小さくなるようにシステムを学習させることで、より精度の高い翻訳が可能になります。
音声認識も、交差エントロピーが活躍する分野の一つです。音声認識とは、人間の声をコンピュータが理解し、テキストデータに変換する技術です。例えば、スマートスピーカーに話しかけた言葉をテキストに変換する際に、コンピュータは、入力された音声データから、様々なテキスト候補を生成し、それぞれの候補がどれくらい正しいかを確率で表します。そして、交差エントロピーを用いて、生成されたテキスト候補と、実際に話された言葉との間のずれを計算し、システムの精度を評価します。
このように、交差エントロピーは、画像認識、自然言語処理、音声認識など、様々な機械学習タスクで、モデルの予測精度を評価し、学習を進めるために欠かせない指標となっています。そして、その汎用性の高さから、今後も様々な分野での活用が期待されています。
| 分野 | タスク例 | 交差エントロピーの役割 |
|---|---|---|
| 画像認識 | 動物の画像分類 | コンピュータの予測(各動物の確率)と正解とのずれを測定 |
| 自然言語処理 | 機械翻訳(日本語から英語) | 生成された英語訳と正しい英語訳とのずれを計算し、システム性能を評価 |
| 音声認識 | 音声のテキスト変換 | 生成されたテキスト候補と話された言葉とのずれを計算し、システム精度を評価 |
