予測精度を測る指標たち

AIを知りたい
先生、正解率・適合率・再現率・F値って、どれも似たように聞こえるんですが、違いがよく分かりません。教えてください。

AIエンジニア
そうだね、似ている用語で紛らわしいよね。例えば、病気かどうかを診断する機械を考えてみよう。正解率は、診断全体のうち、正しく診断できた割合だよ。適合率は、病気と診断された人の中で、実際に病気だった人の割合。再現率は、実際に病気の人の中で、機械が病気と診断できた人の割合だよ。

AIを知りたい
なるほど。それぞれ注目するところが違うんですね。では、F値はどういうものでしょうか?

AIエンジニア
F値は、適合率と再現率のバランスを測る値だよ。病気の診断のように、どちらか一方だけが高ければ良いというわけではない場合に、F値が高いほど、バランス良く予測できていると言えるんだ。
正解率・適合率・再現率・F 値とは。
二つの値で結果を分ける予測において、人工知能の性能を測る指標として『正解率・適合率・再現率・F値』があります。全体の予測のうち、どれくらい正しく予測できたかを表すのが正解率です。人工知能が「正しい」と判断したものの中で、実際に正しいものの割合が適合率です。本当に正しいもの全体の中で、人工知能が「正しい」と判断できたものの割合が再現率です。そして、適合率と再現率のバランスをとった値がF値です。
指標たちの紹介

機械学習の世界では、学習した模型の良し悪しを測る物差しがいくつかあります。特に、二つの答えからどちらかを選ぶ問題では、正解率、適合率、再現率、そしてF値といった物差しがよく使われます。これらはそれぞれ違った角度から模型の出来栄えを調べており、全体的な良し悪しを判断する上で大切な役割を担っています。この記事では、これらの物差しについて詳しく説明し、それぞれの意味やどのように使い分けるのかを深く理解することを目指します。
まず、正解率は、全体の中でどれだけの割合で正解できたかを示す最も基本的な物差しです。しかし、正解と不正解の数が大きく偏っている場合には、正解率だけでは模型の真の実力を測れないことがあります。例えば、めったに起こらない病気の診断では、常に「病気ではない」と答える模型でも高い正解率が出てしまう可能性があります。そこで、適合率が登場します。適合率は、模型が「病気である」と判断した中で、実際に病気だった人の割合を示します。これは、誤った診断を減らす上で重要な指標となります。一方、再現率は、実際に病気だった人の中で、模型が正しく「病気である」と診断できた人の割合を示します。これは、見落としを少なくする上で重要な指標となります。
適合率と再現率は、トレードオフの関係にあることが多く、どちらかを高くしようとすると、もう一方が低くなってしまう傾向があります。例えば、病気の診断で、少しでも疑わしければ「病気である」と判断する模型は、再現率は高くなりますが、適合率は低くなります。逆に、確実な場合のみ「病気である」と判断する模型は、適合率は高くなりますが、再現率は低くなります。そこで、適合率と再現率のバランスを考えた指標がF値です。F値は、適合率と再現率の調和平均であり、両方の指標を同時に高くすることを目指す際に役立ちます。これらの指標の特性を理解することで、より適切な模型選びや改良に繋げることが可能になります。それぞれの指標が持つ意味合いを理解し、状況に応じて適切な指標を用いることで、より精度の高い機械学習模型を構築することができます。
| 指標 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| 正解率 | 全体の中でどれだけの割合で正解できたかを示す。 | 最も基本的な指標。理解しやすい。 | 正解と不正解の数が大きく偏っている場合、真の実力を測れない。 |
| 適合率 | モデルが「陽性」と判断した中で、実際に陽性だったものの割合。 | 誤った陽性診断を減らす上で重要。 | 実際に陽性だったものを見逃す可能性がある。 |
| 再現率 | 実際に陽性だったものの中で、モデルが正しく「陽性」と診断できたものの割合。 | 見落としを少なくする上で重要。 | 誤った陽性診断が増える可能性がある。 |
| F値 | 適合率と再現率の調和平均。 | 適合率と再現率のバランスを考慮。 | 単独ではどちらが高いか低いかわからない。 |
正解率とは

正解率とは、機械学習モデルの性能を測る基本的な指標の一つです。簡単に言うと、モデルがどれだけの割合で正しい予測を行えたかを示す数値です。例えば、100枚の画像から猫と犬を見分けるモデルを作ったとします。このモデルに100枚の画像を見せて、80枚を正しく猫または犬に分類できた場合、このモデルの正解率は80%となります。計算方法は、正解した数 ÷ 全体の予測数 × 100で求められます。
一見すると、正解率が高ければ高いほど良いモデルのように思えます。しかし、扱うデータの性質によっては、正解率だけではモデルの真の性能を正しく評価できない場合があります。例えば、非常に珍しい病気の診断を考えましょう。この病気の患者は全体の1%しかいないとします。もし、常に「病気ではない」と予測するモデルを作った場合、全体の99%の人は実際病気ではないので、このモデルの正解率は99%になります。一見素晴らしいモデルのように見えますが、このモデルは病気の患者を一人も見つけることができません。つまり、病気の早期発見という本来の目的を達成できないのです。
このように、データに偏りがある場合、正解率が高いだけでは不十分です。病気の例のように、少ない割合のデータこそ正しく予測することが重要である場合も多いため、正解率以外の指標も合わせて見て、モデルの性能を総合的に判断する必要があります。
| 指標 | 説明 | 例 | 問題点 |
|---|---|---|---|
| 正解率 | モデルが正しい予測を行えた割合 | 猫と犬の画像分類で80/100枚正解なら正解率80% | データに偏りがある場合、真の性能を反映しない場合がある |
| 正解数 ÷ 全体の予測数 × 100 | 珍しい病気の診断で常に「病気ではない」と予測するモデルは正解率99%だが、患者を一人も見つけられない |
適合率とは
適合率とは、機械学習モデルの性能を測る大切な指標のひとつです。簡単に言うと、ある事柄が「そうだ」と予測されたもののうち、実際に「そうだ」であったものの割合を示します。たとえば、ある果物が「りんご」だと判断された中から、実際にりんごであった割合が適合率にあたります。
もう少し詳しく説明するために、りんごやりんご以外の果物が混ざったかごを想像してみてください。このかごから、りんごと思われるものを選び出す機械があるとします。この機械がりんごを10個選び出し、そのうち8個が本当にりんごだったとしましょう。この場合、機械のりんごに関する適合率は8割、つまり80%となります。残りの2個は、もしかしたらみかんや梨かもしれません。これらは機械がりんごだと誤って判断したものです。
適合率が高いほど、機械が「そうだ」と判断したものの信頼性が高いと言えます。りんごの例で言えば、適合率が高い機械は、りんごだと判断したものが本当にりんごである可能性が高いということです。逆に適合率が低い機械は、りんごではないものをりんごだと誤って判断する可能性が高くなります。
別の例として、迷惑メールの判定を考えてみましょう。迷惑メール判定システムが100通のメールを迷惑メールだと判断し、そのうち80通が実際に迷惑メールだったとします。このシステムの適合率は80%です。残りの20通は、本当は大切なメールだったかもしれません。迷惑メール判定システムでは、高い適合率が求められます。なぜなら、大切なメールを誤って迷惑メールと判断してしまうと、重要な情報を見逃してしまう可能性があるからです。
このように、適合率は様々な場面で活用される重要な指標です。目的や状況に合わせて、他の指標と組み合わせて使うことで、より正確にモデルの性能を評価することができます。
| 例 | 予測が「そうだ」 | 実際に「そうだ」 | 適合率 |
|---|---|---|---|
| りんご判別 | 10個 | 8個 | 80% |
| 迷惑メール判別 | 100通 | 80通 | 80% |
再現率とは

再現率とは、本来あるべきものを見つける能力を測る指標です。具体的には、実際に「正しい」とされるデータ全体の中で、機械学習モデルが「正しい」と予測できた割合を示します。
例えば、ある工場で不良品を見つける検査システムを開発したとします。このシステムで100個の製品を検査し、実際に不良品だったものが10個あったとしましょう。この中で、システムが不良品と正しく判定できた数が8個だった場合、再現率は8/10 = 0.8、つまり80%となります。この数値は、実際に不良品であるもののうち、80%をシステムが見つけられたことを意味します。
別の例として、病院での病気の診断を考えてみましょう。100人の患者を検査し、実際に病気を患っている人が10人いたとします。この中で、医師が正しく病気を診断できた人が8人だった場合、この医師の診断における再現率は80%です。つまり、実際に病気の患者10人のうち、8人を正しく診断できたことになります。
再現率が高いほど、見落としが少なくなるという利点があります。病気の診断で言えば、再現率が高いほど、実際に病気を患っている人を見逃すリスクが低くなります。これは、命に関わるような重大な病気の場合、特に重要です。しかし、再現率だけを高くしようとすると、本来は正常なデータも誤って「正しい」と判定してしまう可能性が高まります。工場の例では、正常な製品を不良品と判定してしまうことが増え、無駄な廃棄につながるかもしれません。病院の例では、健康な人を誤って病気と診断してしまう可能性が高まり、不要な検査や治療につながる可能性があります。そのため、再現率だけでなく、正しいものだけを正しく見つける能力を示す適合率も合わせて考慮することが重要です。両者のバランスをとり、目的に合った適切なモデルを選ぶ必要があります。
| ケース | 全体 | 実際に正しいもの | 正しく予測できたもの | 再現率 |
|---|---|---|---|---|
| 不良品検査 | 100個の製品 | 10個の不良品 | 8個の不良品 | 8/10 = 80% |
| 病気診断 | 100人の患者 | 10人の患者 | 8人の患者 | 8/10 = 80% |
F値とは

「F値」とは、機械学習モデルの性能を測るための大切な指標のひとつです。この指標は、主に分類問題で使われ、「適合率」と「再現率」という二つの指標を組み合わせて計算されます。
まず、「適合率」とは、モデルが「正しい」と判断したものの中で、実際にどれだけが本当に正しかったのかを表す割合です。例えば、あるモデルが10個のリンゴを「赤い」と判断し、そのうち8個が実際に赤いリンゴだった場合、適合率は80%となります。次に、「再現率」とは、実際に「正しい」もの全体の中で、モデルがどれだけの割合を正しく「正しい」と判断できたのかを表す割合です。例えば、全部で15個の赤いリンゴがあり、モデルがそのうち8個を「赤い」と正しく判断できた場合、再現率は約53%となります。
多くの場合、適合率と再現率は、一方を高くしようとするともう一方が低くなるという、いわばシーソーのような関係にあります。例えば、モデルがより多くのリンゴを「赤い」と判断するようにすれば、より多くの赤いリンゴを見つけることができますが、同時に誤って赤いと判断されるリンゴも増えて、適合率は下がる可能性があります。逆に、モデルが「赤い」と判断する基準を厳しくすれば、誤って赤いと判断されるリンゴは減りますが、実際に赤いリンゴを見逃す可能性が高くなり、再現率は下がる可能性があります。
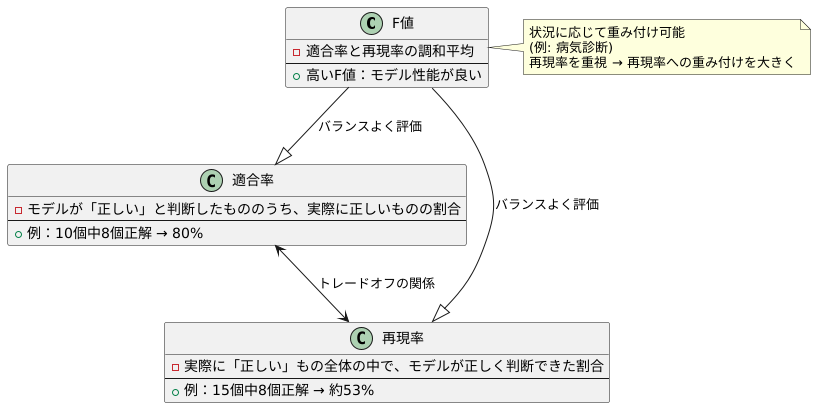
そこで、適合率と再現率の両方をバランスよく評価するために用いられるのが「F値」です。F値は、適合率と再現率の調和平均として計算されます。調和平均は、普通の平均よりも低い値が出やすく、適合率と再現率のどちらか一方が極端に低い場合、F値も低くなります。つまり、F値が高いほど、適合率と再現率のバランスが良く、総合的に見て優れた性能を持つモデルと言えるわけです。
さらに、状況によっては、適合率と再現率に重み付けをしたF値を用いることもあります。例えば、病気の診断のように、たとえ健康な人を誤って病気と診断することがあったとしても、病気の人を見逃さないことが非常に重要な場合、再現率をより重視する必要があります。このような場合には、再現率への重み付けを大きくしたF値を用いることで、より目的に合ったモデル評価を行うことが可能になります。
指標のまとめ

これまで、二値分類問題におけるモデルの性能を測る代表的な指標をいくつか見てきました。具体的には、全体の予測に対する正解の割合を示す正解率、正と予測したデータのうち実際に正であった割合を示す適合率、実際に正であるデータのうち正と予測できた割合を示す再現率、そして適合率と再現率の調和平均であるF値について説明しました。これらの指標はそれぞれ異なる視点からモデルの良し悪しを評価するため、どれか一つだけを見るのではなく、組み合わせて総合的に判断することが大切です。
たとえば、正解率が高いモデルだからといって必ずしも良いモデルとは言えません。なぜなら、データに偏りがある場合、つまり正と負のデータの数が大きく異なる場合、多数派のクラスを常に予測するだけの単純なモデルでも高い正解率が出てしまうからです。このような状況では、正解率はモデルの真の性能を反映しているとは言えません。そこで、適合率や再現率といった他の指標も合わせて検討する必要があるのです。
扱うデータの性質や、モデルを使って何をしたいかによっても、どの指標を重視するかが変わってきます。例えば、健康診断のように病気を見逃すことを極力避けたい、つまり実際に病気の人を病気と診断できる割合を高めたい場合は、再現率を重視すべきです。一方で、迷惑メールの判別のように、普通のメールを誤って迷惑メールと判断してしまうことを減らしたい、つまり迷惑メールと予測したメールが実際に迷惑メールである割合を高めたい場合は、適合率を重視すべきです。このように、それぞれの指標の意味と特徴を正しく理解し、状況に応じて適切な指標を選ぶことで、より良いモデル作りと評価を行うことができます。
| 指標名 | 説明 | 重視する状況 |
|---|---|---|
| 正解率 | 全体の予測に対する正解の割合 | データの偏りがなく、全体的な予測精度を上げたい場合 |
| 適合率 | 正と予測したデータのうち実際に正であった割合 | 偽陽性を減らしたい場合(例: 迷惑メール判別) |
| 再現率 | 実際に正であるデータのうち正と予測できた割合 | 偽陰性を減らしたい場合(例: 健康診断) |
| F値 | 適合率と再現率の調和平均 | 適合率と再現率のバランスを取りたい場合 |
