コスト関数:機械学習モデル最適化の鍵

AIを知りたい
先生、コスト関数ってなんですか?よく聞くんですけど、難しそうでよくわからないです。

AIエンジニア
そうだね。コスト関数は、機械学習のモデルがどれくらい間違っているかを測るものだよ。 例えば、犬と猫を見分けるモデルを作るとするね。このモデルが犬を猫と間違えたら、コスト関数の値は大きくなる。逆に、ちゃんと見分けられたら、値は小さくなるんだ。

AIを知りたい
なるほど。間違えれば値が大きくなって、正解すれば値が小さくなるんですね。でも、その値はどうやって使うんですか?

AIエンジニア
いい質問だね。その値を使って、モデルをより賢くしていくんだ。 コスト関数の値が小さくなるように、モデルのパラメータを調整していく。 例えば、犬と猫を見分けるモデルで、耳の形が重要だとわかったら、耳の形に関するパラメータを調整して、コスト関数の値を小さくしていくんだよ。
コスト関数とは。
人工知能の分野でよく使われる「コスト関数」という言葉について説明します。コスト関数は、機械学習のモデルがどれくらい正確に学習できているかを測るためのものです。学習の際に、正解とのずれ(損失)を計算するための関数で、このずれをできるだけ小さく、あるいは大きくすることで、モデルの精度を上げていきます。
はじめに

機械学習という技術は、まるで人が学ぶように、与えられた情報から隠れた規則や繋がりを見つける力を持っています。膨大な情報の中から法則を掴み取ることで、未来の予測や判断に役立てることができるのです。この機械学習の肝となるのが、学習モデルの良し悪しを測る物差し、すなわちコスト関数です。
コスト関数は、現在の学習モデルがどれくらい正確に予測できているかを数値で表す役割を担っています。学習モデルは、情報から規則性を導き出すために、様々な計算方法を試行錯誤します。この試行錯誤の中で、コスト関数が指し示す数値が小さくなるように、より正確な予測ができるように学習モデルは調整されていきます。
コスト関数の種類は様々で、扱う情報の種類や目的によって使い分けられます。例えば、正解が二択である場合に用いるものや、数値のずれを測るものなど、状況に応じて適切なコスト関数を選ぶことが重要です。
具体的な例を挙げると、明日の気温を予測する学習モデルを考えてみましょう。過去の気温や気象情報から学習し、明日の気温を予測します。この時、実際の気温と予測した気温の差が小さいほど、予測の精度は高いと言えます。この差を計算するのがコスト関数です。学習モデルは、コスト関数の値が小さくなるように、つまり予測のずれが小さくなるように、計算方法を調整していきます。
このように、コスト関数は機械学習の精度向上に欠かせない要素です。コスト関数を理解することで、機械学習の仕組みをより深く理解し、その可能性を最大限に引き出すことができるでしょう。
コスト関数の役割

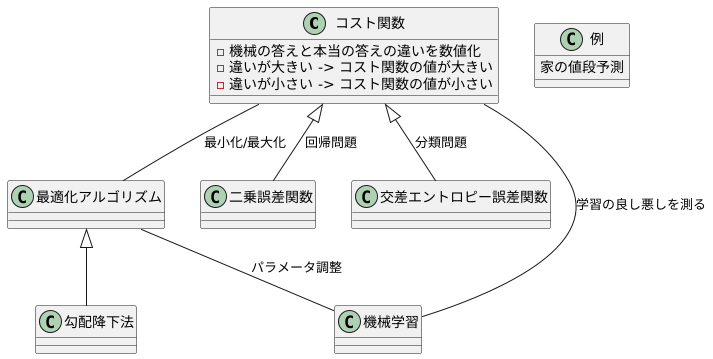
学習する機械の良し悪しを測るものさしとして、コスト関数というものがあります。このものさしは、機械が出した答えと本当の答えとの違いを数値で表すものです。この違いが大きいほど、機械の答えは不正確なので、コスト関数の値も大きくなります。逆に、違いが小さいほど、機械の答えは正確なので、コスト関数の値は小さくなります。
機械学習の目的は、このコスト関数の値をできるだけ小さく、あるいは場合によっては大きくすることです。値を小さくすることで、より正確な答えを出せる機械を作ることができます。例えば、家の値段を予測する機械を考えてみましょう。この機械が予測した値段と実際に売れた値段との差がコスト関数になります。この差を最小にすることで、より正確な値段予測ができる機械を作ることができます。
コスト関数の種類は様々で、状況に合わせて適切なものを選ぶ必要があります。例えば、二乗誤差関数や交差エントロピー誤差関数などがあります。二乗誤差関数は、予測値と実測値の差の二乗の和を計算するもので、回帰問題によく用いられます。一方、交差エントロピー誤差関数は、分類問題によく用いられ、予測された確率分布と実際の確率分布との違いを測るものです。
コスト関数を最小にするためには、最適化アルゴリズムと呼ばれる手法を用います。この手法は、少しずつ機械の調整を行いながら、コスト関数の値が最小になる方向を探し出すものです。代表的な最適化アルゴリズムとしては、勾配降下法などがあります。勾配降下法は、山を下るように、コスト関数が最小になる方向へ少しずつパラメータを調整していく方法です。
このように、コスト関数は機械学習において重要な役割を果たしており、適切なコスト関数と最適化アルゴリズムを選ぶことで、より精度の高い機械を作ることができます。
様々な種類のコスト関数

機械学習において、コスト関数はモデルの性能を評価する重要な指標です。この関数は、モデルの予測値と実際の値との差を数値化し、モデルの学習において最適なパラメータを見つけるために利用されます。様々な種類のコスト関数があり、それぞれ異なる特性と用途を持っています。
まず、代表的なコスト関数の一つに平均二乗誤差があります。これは、予測値と実測値の差を二乗し、その平均を計算することで得られます。この関数は、誤差を二乗することで大きな誤差をより強調するため、外れ値の影響を受けやすいという特徴があります。主に、連続値を予測する回帰問題で使用されます。例えば、住宅価格の予測や売上予測など、実数値を予測する際に用いられます。
次に、分類問題でよく用いられるのが交差エントロピー誤差です。これは、予測された確率分布と実際の確率分布の差を測定するものです。複数の選択肢から一つを選ぶような多クラス分類問題に適しており、画像認識や自然言語処理などで広く使われています。例えば、手書き数字認識において、モデルが数字「3」を「8」と誤認識した場合、この誤差は大きくなります。
コスト関数の選択は、解く問題の種類やデータの特性によって大きく影響を受けます。例えば、外れ値の影響が少ないロバストな推定をしたい場合は、平均絶対誤差を用いることが適切です。また、画像認識のように多数のクラスに分類する問題では、交差エントロピー誤差が有効です。これらの関数の特性を理解し、適切な関数を選択することで、より精度の高いモデルを構築することができます。
さらに、コスト関数には、上記以外にも、ヒンジ損失やハミング損失など様々な種類が存在します。それぞれの関数の特性を理解し、問題に合わせて適切なコスト関数を選択することが、機械学習モデルの性能向上に不可欠です。
| コスト関数名 | 説明 | 用途 | 例 | 特徴 |
|---|---|---|---|---|
| 平均二乗誤差 | 予測値と実測値の差を二乗し、その平均を計算。 | 回帰問題(連続値予測) | 住宅価格予測、売上予測 | 大きな誤差を強調、外れ値の影響を受けやすい |
| 交差エントロピー誤差 | 予測された確率分布と実際の確率分布の差を測定。 | 分類問題(多クラス分類) | 画像認識、自然言語処理、手書き数字認識 | 複数の選択肢から一つを選ぶ問題に適している |
| 平均絶対誤差 | 予測値と実測値の差の絶対値の平均を計算。 | 回帰問題(連続値予測) | 外れ値の影響を受けにくい推定 | 外れ値の影響が少ないロバストな推定 |
| ヒンジ損失 | – | – | – | – |
| ハミング損失 | – | – | – | – |
最適化手法との関連

望ましい結果を得るための手順を最適化手法と呼びます。この手法は、ある特定の値を最小にしたり最大にすることを目指します。この特定の値は、状況や目的によって様々ですが、一般的には費用や損失、あるいは利益や効率といったものに対応します。
最適化を行うための代表的な方法として、勾配降下法と確率的勾配降下法が挙げられます。これらの方法は、特定の値が小さくなるように少しずつ調整を繰り返すことで最適な状態を見つけ出します。
勾配降下法は、山の斜面を下る動きに例えることができます。山頂から谷底に向かうには、常に最も急な斜面を下るのが近道です。この最も急な斜面の方向は、勾配と呼ばれる数値で表されます。勾配が大きい、つまり斜面が急な場合は大きく一歩を踏み出し、勾配が小さい、つまり斜面が緩やかな場合は小さく一歩を踏み出します。この一歩一歩の大きさで調整の度合いを決め、少しずつ谷底に近づいていくのです。そして最終的に谷底、つまり最も低い場所にたどり着いた時に、目的としていた値も最小となります。これが勾配降下法による最適化です。
確率的勾配降下法も、基本的な考え方は勾配降下法と同じです。しかし、毎回全ての情報を用いて勾配を計算するのではなく、一部の情報だけを使って勾配を計算し調整を行います。そのため、計算の手間が少なく、効率的に最適化を進めることができます。ただし、一部の情報だけを使うため、勾配の計算に誤差が生じる可能性があり、その結果、最適な値にたどり着くまでに時間がかかったり、少しずれた値に落ち着いてしまうこともあります。どの手法が適しているかは、状況に応じて判断する必要があります。
過学習と正則化

機械学習の目的は、未知のデータに対して正確な予測を行うことです。しかし、学習に用いるデータに過剰に適合しすぎてしまうと、新しいデータへの対応力が失われ、期待通りの予測精度が得られなくなってしまいます。これが過学習と呼ばれる現象です。まるで、特定の問題集の解答だけを暗記してしまい、応用問題が解けなくなってしまう生徒のような状態です。
過学習は、モデルが学習データの細かな特徴や、本来は無視すべき雑音までも学習してしまうことで起こります。例えるなら、木の葉一枚一枚の形まで覚えて森全体を把握しようとするようなものです。これでは、新しい森を見た時に、葉の形の違いに惑わされて森全体を見失ってしまいます。
この過学習を防ぐための有効な手段として、正則化という手法があります。正則化は、モデルの複雑さを抑えることで、過学習を抑制する役割を果たします。具体的には、モデルのパラメータの値が大きくなりすぎるのを防ぎ、滑らかで汎化性能の高いモデルを構築します。これは、森全体の形を把握することに集中し、個々の木の葉の詳細に囚われ過ぎないようにするようなものです。
正則化には様々な種類があり、代表的なものとしてL1正則化とL2正則化が挙げられます。L1正則化は、不要なパラメータをゼロに近づける効果があり、モデルを簡素化するのに役立ちます。一方、L2正則化は、全てのパラメータをバランス良く小さくすることで、モデルの滑らかさを促進します。どの正則化手法を用いるかは、扱うデータやモデルの特性によって適切に選択する必要があります。
正則化は、過学習を防ぎ、未知のデータに対する予測精度を向上させるための重要な技術です。適切な正則化手法を用いることで、より信頼性の高い機械学習モデルを構築することができます。
| 問題 | 過学習 | 対策 | 手法 | 効果 |
|---|---|---|---|---|
| 未知のデータに対する予測精度を高めたい | 学習データに過剰に適合し、新しいデータへの対応力が失われる | 正則化 | L1正則化 | 不要なパラメータをゼロに近づけ、モデルを簡素化 |
| L2正則化 | 全てのパラメータをバランス良く小さくし、モデルの滑らかさを促進 |
まとめ

機械学習は、まるで人間の学習と同じように、コンピュータにデータからパターンを見つける能力を与える技術です。この学習プロセスにおいて、コンピュータがどれだけうまく学習できているかを測るための重要な尺度となるのが「コスト関数」です。コスト関数は、予測値と実際の値との間のずれを数値化し、このずれが小さいほど、モデルの精度が高いことを示します。
コスト関数の種類は様々で、目的に応じて使い分ける必要があります。例えば、回帰問題では、予測値と実測値の差の二乗和を計算する「二乗誤差」がよく用いられます。一方、分類問題では、予測の確からしさを表す確率を用いて計算する「対数損失」などが使われます。どのコスト関数を採用するかは、扱うデータの性質や、解決したい問題の種類によって慎重に検討する必要があります。
コスト関数の値を最小にすることが、機械学習の目標です。そのためには、様々な計算方法を用いて、モデルのパラメータを調整していきます。この調整作業は「最適化」と呼ばれ、勾配降下法などの手法が用いられます。勾配降下法は、山を下るように、コスト関数の値が最も小さくなる方向へパラメータを少しずつ調整していく方法です。
さらに、モデルが学習データに過剰に適応してしまう「過学習」を防ぐために、正則化という技術が用いられます。正則化は、モデルのパラメータが大きくなりすぎるのを防ぎ、汎化性能を高める効果があります。コスト関数に正則化項を加えることで、過学習を抑え、未知のデータに対しても精度高く予測できるモデルを作ることができます。
つまり、コスト関数は単なる評価指標ではなく、機械学習モデルの学習プロセスの中核を担う重要な要素なのです。コスト関数の種類や仕組みを理解し、最適化手法や正則化と組み合わせることで、より高精度で実用的な機械学習モデルを構築することが可能になります。
