自己符号化器:データの圧縮と復元

AIを知りたい
先生、「自己符号化器」って、入力したものと同じものを出力するように学習するんですよね?でも、それってただ同じものを返すだけで、何か意味があるんですか?

AIエンジニア
いい質問だね。確かに、ただ同じものを返すだけだと意味がないように見えるよね。ポイントは「隠れ層」にあるんだ。隠れ層の大きさは入力層より小さい。つまり、少ない情報で元の情報を復元しようとしているんだよ。

AIを知りたい
少ない情報で復元する?それって、どういうことですか?

AIエンジニア
たとえば、たくさんの数字の列から重要な特徴だけを抜き出して、少ない数字で元の数字の列を復元するようなイメージだよ。だから、自己符号化器はデータの重要な特徴を学習するのに役立つんだ。
自己符号化器とは。
人工知能の用語で『自己符号化器』というものがあります。これは、入力されたものと同じものを出力するように学習する方法です。一般的には、入力層よりも隠れ層の次元数が小さくなるような構造をしています。このような構造のため、入力されたデータの情報が圧縮され(符号化)、その圧縮されたデータから元のデータを復元する(復号化)という働きをしています。
自己符号化器とは

自己符号化器とは、機械学習の中でも、教師なし学習と呼ばれる分野に属する技術です。まるで写し鏡のように、入力された情報をそのまま出力するように学習することで、データの隠れた特徴を捉えることができます。
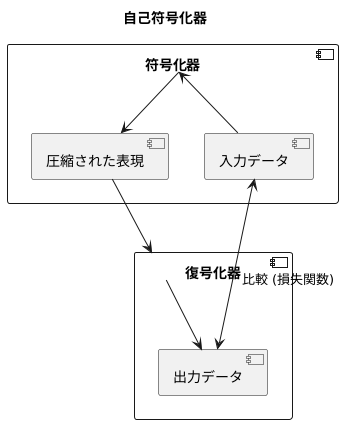
具体的には、自己符号化器は符号化器と復号化器という二つの部分から構成されています。まず、符号化器が入力データを受け取り、それをより小さな次元、つまり圧縮された表現に変換します。この圧縮された表現は、入力データの本質的な特徴を抽出したものと考えることができます。次に、復号化器がこの圧縮された表現を受け取り、元の入力データとできるだけ同じになるように復元します。
学習の過程では、入力データと復号化器が出力したデータの違いを小さくするように、符号化器と復号化器のパラメータを調整していきます。この違いは、一般的に損失関数と呼ばれるもので測られます。損失関数の値が小さくなるように学習を進めることで、自己符号化器はデータの特徴を効果的に捉えることができるようになります。
自己符号化器は、一見単純な仕組みながら、様々な応用が可能です。例えば、高次元データの次元を削減することで、計算コストを削減したり、データの可視化を容易にすることができます。また、ノイズの多いデータからノイズを取り除いたり、正常なデータとは異なる異常なデータを検知するのにも利用できます。さらに、画像の生成や欠損データの補完など、より高度なタスクにも応用されています。このように、自己符号化器はデータ分析において強力な道具となるため、幅広い分野で活用が期待されています。
データの圧縮

情報の詰め込みすぎは、時に物事を分かりにくくしてしまいます。膨大な資料の山の中から必要な情報を探し出すのは大変な作業ですし、大きな荷物を運ぶのも一苦労です。コンピュータの世界でも同じことが言えます。データ量が大きすぎると、保存するための場所がたくさん必要になり、処理にも時間がかかってしまいます。そこで役立つのが「データの圧縮」です。
自己符号化器は、このデータ圧縮において重要な役割を担っています。自己符号化器とは、入力されたデータの特徴を学習し、それをより少ない情報量で表現する技術です。例えるなら、長い文章を要約するようなものです。元の文章と同じ内容を、より短い言葉で表現することで、情報量は減りますが、重要な点はしっかりと残ります。
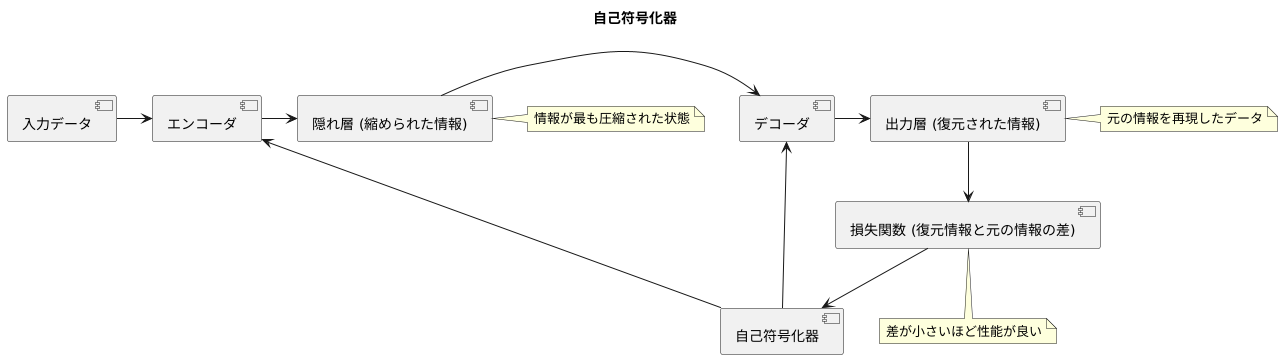
自己符号化器の仕組みは、少し複雑です。まず、入力データは「符号化」という過程を経て、より少ない次元、つまり情報量を持つ「隠れ層」と呼ばれる部分へと変換されます。この隠れ層は、入力データの持つ本質的な情報のみを抽出した、いわば「要点」のようなものです。そして、この「要点」から元のデータにできるだけ近い情報を復元する「復号化」という過程を経て、出力データが生成されます。
隠れ層の次元数は、入力データの次元数よりも小さくなっています。これがデータ圧縮の鍵です。高次元データ、つまり情報量の多いデータは、隠れ層を通して低次元データ、つまり情報量の少ないデータに変換されることで、容量が小さくなり、処理も速くなります。まるで、大きな荷物を小さな箱に詰め替えるようなものです。
このように、自己符号化器はデータの要点だけを抽出して表現することで、データの圧縮を実現し、保存容量の削減や処理速度の向上に貢献しています。これは、膨大なデータを扱う現代社会において、大変重要な技術と言えるでしょう。
データの復元

縮められた情報は、元の形に戻すことができます。 この作業は、自己符号化器と呼ばれる仕組みを使って行います。自己符号化器は、縮められた情報を元の情報に近づけるように、段階的に情報を広げていきます。
まず、情報はギュッと詰め込まれた状態になっています。 これを、自己符号化器の中間地点である隠れ層と呼びます。隠れ層から出力層と呼ばれる最後の段階まで、情報は徐々に広げられていきます。この広げる過程で、自己符号化器は、縮められた情報から元の情報の大切な特徴を再現しようとします。
しかし、完全に元の情報と同じように再現できるとは限りません。 例えるなら、折り紙を一度折ってから開くと、折り目が残ってしまうように、情報も縮める過程で多少の変化が起きてしまうからです。ただし、自己符号化器は学習を重ねることで、より元の情報に近い形に復元できるようになります。折り紙の達人が、より綺麗に折り目を目立たなくできるように、学習によって復元の精度が上がっていくのです。
復元された情報と元の情報の差が小さいほど、自己符号化器の性能が良いと言えます。 これは、自己符号化器が情報の大切な特徴をうまく捉え、上手に縮めて、そして元に戻せていることを示しているからです。この差を小さくするために、自己符号化器は損失関数と呼ばれる指標を用いて、常に性能の向上を目指して学習を続けていきます。 損失関数は、復元された情報と元の情報の差を数値で表したもので、この数値が小さいほど、復元の精度が高いことを意味します。自己符号化器は、この損失関数を最小にするように学習することで、より正確に情報を復元できるようになるのです。
次元削減

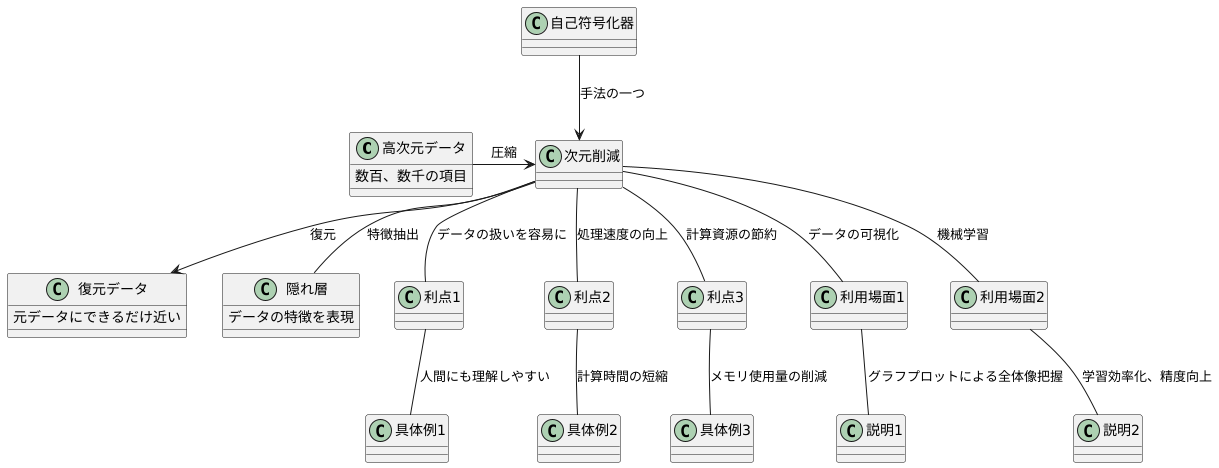
多くの情報を持つデータは、そのままでは扱うのが難しい場合があります。 例えば、数百、数千もの項目について情報を持っているデータは、全体像を把握しにくく、計算にも時間がかかります。このような高次元データを、重要な情報だけを保ったまま、より少ない項目数で表現する方法が次元削減です。
次元削減を実現する技術の一つとして、自己符号化器があります。自己符号化器は、入力されたデータを一度圧縮し、その後、元のデータにできるだけ近い形に復元するように学習します。この学習過程で、データの特徴を最もよく表す隠れ層と呼ばれる部分が形成されます。この隠れ層は、元のデータよりも少ない項目数で表現されているため、次元削減を実現できます。
次元削減の利点は、データの扱いを容易にすることです。例えば、数百の項目で表されていたデータを数十の項目に削減できれば、人間にも理解しやすくなります。また、計算に用いるデータ量が減るため、処理速度の向上や計算資源の節約に繋がります。
次元削減されたデータは、様々な場面で役立ちます。複雑なデータの関係性を視覚的に捉えたい場合、次元削減によって2次元や3次元までデータの項目数を減らすことで、グラフなどにプロットして全体像を把握できます。また、機械学習のアルゴリズムにデータを入力する際にも、次元削減は有効です。項目数が減ることで学習が効率化され、精度の向上が期待できます。
このように、次元削減は、データ解析において重要な役割を担う技術と言えるでしょう。
応用例

自己符号化器は、様々な分野で応用されています。まるで写し絵のように、入力された情報を一度圧縮し、それから元の形に戻す仕組みを持つこの技術は、多くの場面で力を発揮しています。
まず、画像処理の分野を見てみましょう。写真に写り込んだ不要なノイズ、例えば小さなゴミやざらつきを取り除くのに、自己符号化器は役立ちます。ノイズを含んだ画像を入力すると、自己符号化器はその特徴を学習し、ノイズを取り除いた綺麗な画像を生成します。まるで職人のように、画像の細部まで丁寧に修正してくれるのです。また、画像を新しく作り出す、いわゆる画像生成の分野でも活躍しています。学習データに基づいて、新しい画像を生み出すことができるため、芸術創作やデザインの分野でも期待されています。
次に、異常検知の分野です。工場の機械やシステムの監視など、正常な状態からの逸脱をいち早く察知することは非常に重要です。自己符号化器は、あらかじめ正常なデータの特徴を学習します。そして、新たなデータが入力された際に、学習した正常なデータと比較し、大きな違いがあれば異常と判断します。例えば、いつもと違う機械の振動やシステムの負荷などを検知し、故障の予兆を掴むことができます。これはまるで番人のように、システムの安全を守っていると言えるでしょう。
さらに、ネットショッピングなどでよく見かける推薦システムにも、自己符号化器は活用されています。膨大な商品データの中から、個々のユーザーの好みに合った商品を選び出すのは至難の業です。自己符号化器は、ユーザーの過去の購買履歴や閲覧履歴などのデータから、そのユーザーが好むであろう潜在的な特徴を捉えます。そして、その特徴に合致する商品を推薦することで、ユーザーの購買体験を向上させます。まるで優秀な販売員のように、一人ひとりの顧客に最適な商品を提案してくれるのです。
このように、自己符号化器は様々な分野で応用され、私たちの生活を豊かにしています。今後、技術の進歩とともに、さらに多くの分野で活躍していくことでしょう。
| 分野 | 用途 | 説明 |
|---|---|---|
| 画像処理 | ノイズ除去 | ノイズを含んだ画像を入力し、ノイズを取り除いた綺麗な画像を生成 |
| 画像処理 | 画像生成 | 学習データに基づいて新しい画像を生成 |
| 異常検知 | システム監視 | 正常なデータから学習し、異常なデータとの違いを検知 |
| 推薦システム | 商品推薦 | ユーザーのデータから潜在的な特徴を捉え、商品を推薦 |
学習方法

自己符号化器の学習には、教師なし学習と呼ばれる手法が使われます。教師なし学習とは、名前の通り教師となるデータ、つまり正解となる出力データ無しで学習を進める方法です。通常の学習では入力データと正解となる出力データの組をいくつも与えて学習しますが、教師なし学習では入力データのみを与えます。自己符号化器の場合、入力データがそのまま出力データの代わりとなるため、教師なし学習が使えるのです。
では、どのように学習を進めるのでしょうか。自己符号化器は、入力データを受け取ると、それをいったんより少ない情報量で表現するように圧縮します。この圧縮された表現は、いわばデータの重要な特徴を抽出したものと言えます。そして、この圧縮された情報から元の入力データを復元しようと試みます。学習の目的は、復元されたデータが入力データになるべく近づくようにすることです。
入力データと復元されたデータの差を損失と言い、この損失を小さくすることが学習の目標となります。損失を計算する方法は様々ですが、一般的には二乗誤差などが用いられます。二乗誤差とは、入力データと復元されたデータの各要素の差を二乗し、それらをすべて足し合わせたものです。この損失の値が小さければ小さいほど、復元されたデータが入力データに近く、うまく学習が進んでいることを示します。
損失を小さくするために、自己符号化器は内部のパラメータを調整します。このパラメータは、人間の脳でいうシナプスの結合の強さに相当するもので、入力データがどのように処理されるかを決定づけます。パラメータの調整には、逆誤差伝播法などの最適化手法が用いられます。逆誤差伝播法は、損失の値に基づいて、どのパラメータをどのように調整すれば損失がより小さくなるかを計算する、効率的なアルゴリズムです。
このように、自己符号化器は入力データと復元されたデータの差を小さくするように、何度もパラメータを調整し学習を進めることで、データの特徴をうまく捉えられるようになります。学習が完了した自己符号化器は、データの圧縮と復元を高い精度で行えるようになり、様々な応用が期待できます。