データの自動分類:クラスタ分析入門

AIを知りたい
先生、クラスタ分析ってなんですか?

AIエンジニア
クラスタ分析とは、似ているもの同士をグループ分けする手法のことだよ。例えば、果物を大きさや色でグループ分けすると、りんご、みかん、ぶどうなどのグループができるようなイメージだね。これをデータに対して行うのがクラスタ分析だ。

AIを知りたい
k-means法というのは、どういうものなのでしょうか?

AIエンジニア
k-means法は、あらかじめいくつのグループに分けるか(k個)を決めて、データをk個のグループに分ける方法だよ。それぞれのグループの中心点を計算し、データがどの中心点に一番近いかでグループ分けするんだ。中心点はデータの配置によって移動していくから、最終的に最適なグループ分けができるように計算を繰り返すんだよ。
クラスタ分析とは。
人工知能にまつわる言葉で「集団分け分析」というものがあります。これは、人間が教えなくてもコンピューターが自分で学習するタイプの分析方法の一つです。データをいくつかの集団(かたまり)に分けるやり方の一つに、k平均法と呼ばれるものがあり、この方法を使った分析を「集団分け分析」と呼びます。
集団分けの仕組み

集団分けの仕組みは、多くの情報を整理し、意味のあるまとまりを見つけるための方法です。物事の集まりを、似ているもの同士でグループ化する作業を、集団分けと呼びます。この集団分けは、私たちの日常の中でも、例えばスーパーマーケットの商品棚のように、無意識に行われています。野菜売り場、果物売り場、肉売り場など、商品を種類ごとに並べることで、買い物客は目的の品を簡単に見つけることができます。
データの分析においても、集団分けは重要な役割を果たします。膨大なデータの中から、隠れた規則性や特徴を見つけるために、似た性質を持つデータを自動的にグループ化する技術が、集団分けの仕組みです。この仕組みは、専門的には「集団分析」と呼ばれ、様々な分野で活用されています。
例えば、顧客の購買履歴を分析する場合、集団分けによって顧客をいくつかのグループに分類できます。過去の購入商品や購入金額などから、似たような購買傾向を持つ顧客を同じグループにまとめることで、それぞれのグループに合わせた販売戦略を立てることができます。あるグループには新商品の案内を、別のグループには割引情報を提供するなど、より効果的な販売促進活動が可能になります。
また、医療の分野でも、集団分けは病気の診断に役立てられています。患者の症状や検査結果などのデータから、似たような症状を持つ患者をグループ分けすることで、病気の種類を特定しやすくなります。さらに、新しい薬の開発にも、集団分けは欠かせません。薬の効果を検証する際、被験者を適切なグループに分けることで、より正確な結果を得ることができます。
このように、集団分けは、大量のデータの中から価値ある情報を見つけ出すための強力な道具と言えるでしょう。様々な計算方法を用いて、データ間の「近さ」を測り、最適なグループ分けを実現します。データの性質や分析の目的に合わせて、適切な方法を選ぶことが重要です。
| 分野 | 集団分けの例 | 利点 |
|---|---|---|
| 日常生活 | スーパーマーケットの商品棚 (野菜、果物、肉など) | 買い物客が目的の品を簡単に見つけられる |
| データ分析 (顧客分析) | 顧客の購買履歴に基づいたグループ分け (購入商品、購入金額など) | グループに合わせた販売戦略が可能 (新商品案内、割引情報など) |
| 医療 | 患者の症状や検査結果に基づいたグループ分け | 病気の診断、新薬開発 |
代表的手法:k-means法

集団をいくつかの似た者同士の小さな集団に分ける作業、すなわち集団分け分析には様々なやり方がありますが、その中でもよく知られて広く使われているのが、今回の話題である「k平均法」です。k平均法は、まず初めにいくつの小さな集団に分けたいか、その数を決めます。この数を「k」という記号で表します。例えば、全体を3つの集団に分けたい場合は、kに3という値を指定します。
次に、分けたい対象となるデータの中から、無作為にk個のデータを選び出します。kが3であれば、3つのデータを選び出すことになります。これらの選ばれたデータは、それぞれの小さな集団の中心となる点、つまり中心点の最初の位置として扱われます。
中心点が定まると、今度はそれぞれのデータがどの小さな集団に属するかを調べます。具体的な手順としては、個々のデータと中心点との間の距離を計算し、どのデータも自分に一番近い中心点の小さな集団に所属するように割り振ります。
全てのデータの所属先が決まったら、各集団に属するデータの平均値を計算し、それを新たな中心点とします。中心点が移動したため、もう一度各データと中心点との距離を計算し、最も近い中心点の集団に再度割り当てを行います。
この、中心点の再計算とデータの再割り当てという一連の作業を、中心点が動かなくなるか、あらかじめ決めておいた回数繰り返すことで、最終的にデータの集団分けが完了します。k平均法は計算方法が比較的単純で、大量のデータにも対応できるため、様々な分野で活用されています。
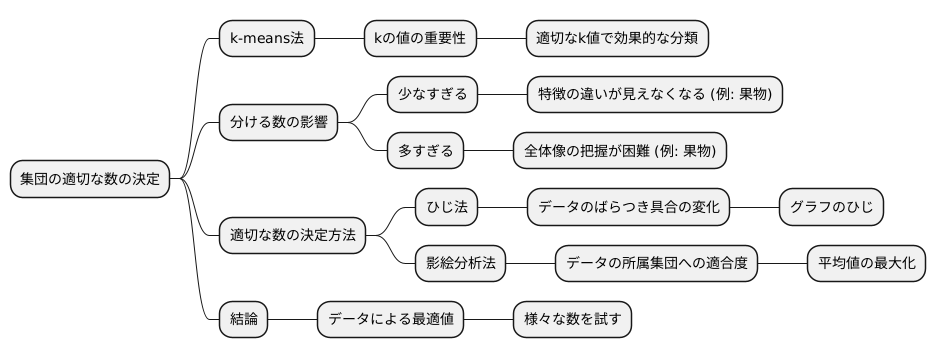
適切な集団数の決め方

集団を適切な数に分割することは、物事を分類する上で非常に大切です。例えば、顧客をグループ分けして販売戦略を立てたり、商品の種類分けで在庫管理をしたりする際に、集団の数が適切でないと、効果的な分析や管理をすることができません。
「k-means法」という、データを自動的に分類する便利な手法がありますが、この手法で重要なのは、あらかじめいくつの集団に分けるか(kの値)を決めておくことです。この数を適切に選ばないと、せっかくの分類作業がうまくいかないことがあります。
もし、分ける数が少なすぎると、本来は別々の特徴を持つデータが同じ集団にまとめられてしまい、重要な違いが見えなくなってしまう可能性があります。例えば、様々な種類の果物を「甘い」と「酸っぱい」の二つの集団に分けるだけでは、りんご、みかん、ぶどうといった果物ごとの特徴を捉えることができません。
反対に、分ける数が多すぎると、似ているデータが別々の集団に分けられてしまい、全体像が把握しにくくなります。果物を「赤いりんご」「青いりんご」「赤いみかん」など、細かく分けすぎると、果物全体の傾向を掴むのが難しくなります。
では、どうやって適切な集団の数を見つけるのでしょうか?「ひじ法」と「影絵分析法」という二つの方法がよく使われます。「ひじ法」は、集団の数を変えながら、各集団の中でのデータのばらつき具合を測り、その変化が最も大きいところが適切な集団の数だと判断する方法です。グラフにすると、ちょうどひじのように折れ曲がっているところが最適な数になります。「影絵分析法」は、それぞれのデータが、自分が所属する集団にどれだけうまく当てはまっているかを数値化し、その平均値が最も高くなる集団の数が最適だと判断する方法です。
最適な集団の数は、扱うデータによって様々です。そのため、色々な数を試してみて、データの特徴をうまく捉えられる数を見つけることが大切です。
データの準備と注意点

集団分けの分析を行うにあたって、適切な準備と注意すべき点があります。まず、分析に使う情報の準備です。集めた情報の中に欠けている部分がある場合は、その部分を補うか、欠けている情報を含むデータ自体を取り除く必要があります。データに欠損があると、分析結果に悪影響を与える可能性があります。
次に、情報の単位や大きさが異なる場合の対応です。例えば、あるデータはキロメートル単位、別のデータはメートル単位で記録されている場合、そのままでは比較できません。このような場合は、標準化や正規化といった処理で、データの単位や大きさを揃える必要があります。データの尺度が揃っていないと、分析結果が歪んでしまう可能性があります。
また、集めた情報の中に、他の値から大きく外れた値、いわゆる外れ値が含まれている場合があります。外れ値は分析結果に大きな影響を与えるため、外れ値を取り除くか、外れ値の影響を受けにくい分析手法を用いる必要があります。具体的には、外れ値を特定し、分析対象から除外するか、外れ値の影響を軽減するような特別な計算方法を使う必要があります。
さらに、よく使われる「K平均法」という集団分けの方法では、集団の中心となる点の選び方によって結果が変わるという特性があります。そのため、分析を複数回実行し、その結果を比較することで、より信頼性の高い結果を得ることができます。
最後に、K平均法は、丸い形の集団を想定した分析手法です。そのため、複雑な形の集団にはうまく対応できない場合があります。もし、分析対象の集団が複雑な形をしている場合は、K平均法以外の、より適切な分析手法を検討する必要があります。色々な手法を試すことで、データの特性に合った最適な分析結果を得ることができます。
| 手順 | 注意点 | 対応策 |
|---|---|---|
| 情報の準備 | 欠損値 | 欠損値を補完するか、欠損データを除外 |
| 情報の準備 | 単位・大きさの不一致 | 標準化または正規化 |
| 情報の準備 | 外れ値 | 外れ値を除外、または外れ値の影響を受けにくい分析手法 |
| K平均法の実行 | 中心点の選び方で結果が変わる | 複数回実行し結果を比較 |
| K平均法の実行 | 丸い形の集団を想定 | 複雑な形の集団には不向き。別の分析手法を検討 |
活用の場

集団分けの技法は、様々な場所で役立っています。販売促進の場では、顧客をいくつかの集団に分け、的を絞った広告や商品の提案に用いられています。例えば、顧客の過去の買い物や顧客の特徴から集団分けを行い、顧客の要望に合ったサービスを提供することで、顧客の満足度を高め、売り上げを伸ばすことに繋がります。
医療の場では、患者の症状から病気の種類を見分け、診断や治療方針を決めるのに役立っています。例えば、似た症状を持つ患者を同じ集団にまとめることで、病気の進行度合いを予測したり、より効果的な治療法を見つけ出すのに役立ちます。
写真の解析の場では、写真を小さな点ごとに調べ、写真の領域分けや物の認識に役立っています。例えば、空や木、建物といった異なる領域を自動的に見分けることができます。また、写真に写っている物体が何かを判断するのにも役立ちます。
お金のやり取りの場では、顧客の信用度を評価したり、不正を見つけるのにも役立っています。例えば、過去の取引履歴や返済能力から顧客をグループ分けし、融資の可否判断などに活用されています。また、普段と異なる取引パターンを検知することで、不正利用の可能性を早期に発見することが可能になります。
このように、集団分けの技法は多くの場所で重要な役割を担っており、これからさらに活用範囲が広がることが見込まれます。情報がどんどん増える現代社会において、集団分けの技法は情報の奥にある隠れた規則性を見つけ、より良い判断をするための強力な道具となるでしょう。
| 分野 | 活用例 | 効果 |
|---|---|---|
| 販売促進 | 顧客をグループ分けし、ターゲットを絞った広告や商品提案を行う。 | 顧客満足度向上、売上増加 |
| 医療 | 患者の症状から病気の種類を見分け、診断や治療方針を決める。 | 病気の進行予測、効果的な治療法の発見 |
| 写真の解析 | 写真の領域分け、物の認識 | 空や木、建物といった異なる領域の自動判別、写真に写っている物体の判断 |
| お金のやり取り | 顧客の信用度評価、不正検知 | 融資の可否判断、不正利用の早期発見 |
