ウォード法:データの分類を最適化

AIを知りたい
先生、「ウォード法」ってよく聞くんですけど、具体的にどんなものなんですか?

AIエンジニア
簡単に言うと、データの集まりを似たもの同士でグループ分けする時の方法の1つだよ。例えば、果物を種類ごとにまとめていくようなイメージだね。ウォード法は、グループ分けする際に、グループ全体のばらつきがなるべく小さくなるようにするんだ。

AIを知りたい
ばらつきを小さくする、というのはどういうことですか?

AIエンジニア
例えば、りんご同士、みかん同士でグループを作る際に、りんごの中にみかんが1つ混ざってしまうと、そのグループのばらつきは大きくなるよね?ウォード法は、そういったばらつきが最小になるように、グループを作っていく方法なんだ。計算に時間はかかるけど、精度の高いグループ分けができるから、よく使われているんだよ。
ウォード法とは。
人工知能でよく使われる言葉に『ウォード法』というものがあります。これは、階層的に集団を分けていく分析方法のひとつです。まず、『集団分け』とは、簡単に言うとデータなどの集まりを、役割や種類ごとに分けて集めることです。集団分けをするためのやり方には大きく分けて2種類あり、そのうちの1つが階層的に集団を分けていく分析方法です。ウォード法では、2つの集団(仮にPとQとします)をくっつけたと考えてみます。くっつけたことで、集団の中心と、集団の中のそれぞれのデータとの間の距離の二乗を合計した値(これをくっつけた後の集団P∪QでL(P∪Q)とします)と、元々の2つの集団PとQそれぞれで、中心とそれぞれのデータとの間の距離の二乗を合計した値、L(P)とL(Q)を比べてみます。くっつけた後の値L(P∪Q)から、くっつける前の値L(P)とL(Q)をひいた差が、できるだけ小さくなるように集団同士をくっつけていくのがウォード法です。計算に時間はかかりますが、分ける精度がとても良いので、よく使われています。
分類の基礎

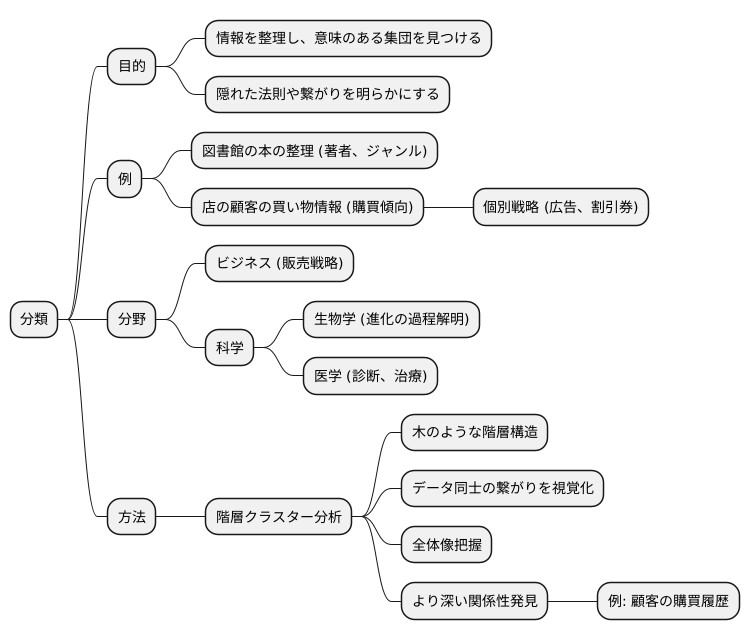
情報を整理し、意味のある集団を見つける作業は、データ分析においてとても重要です。この作業を分類と言い、大量の情報から隠れた法則や繋がりを明らかにするのに役立ちます。分類は、まるで図書館でたくさんの本を著者やジャンルごとに整理して並べるようなものです。整理されていない大量の本の中から目的の本を見つけるのは大変ですが、きちんと分類されていれば探し出すのも容易になります。
例えば、お店の顧客の買い物情報を考えてみましょう。誰が何をいつ買ったのかというバラバラの情報は、そのままでは宝の持ち腐れです。しかし、顧客を買い物傾向に基づいてグループ分けすれば、それぞれの集団に合わせた販売戦略を立てることができます。よくお菓子を買う集団には新商品のお菓子の広告を、健康食品をよく買う集団には健康に良い商品の割引券を送るといった具合です。このように、分類は商売の戦略を考える上で大きな武器となります。
分類の使い道はビジネスに限らず、科学の分野でも様々です。例えば、生物学では生物を様々な特徴に基づいて分類することで進化の過程を解明したり、医学では患者の症状を基に病気を分類することで診断や治療に役立てたりしています。
分類を行うための方法はいくつかありますが、階層クラスター分析はその中でも有力な方法の一つです。これは、データを木のような階層構造で分類する方法で、まるで家系図のようにデータ同士の繋がりを視覚的に分かりやすく示してくれます。階層クラスター分析を使うことで、全体像を把握しながら、データのより深い関係性を発見することができます。例えば、顧客の購買履歴を階層クラスター分析で分類すれば、一見バラバラに見える顧客集団の中に、共通の購買パターンを持つ小さな集団が隠れていることを見つけることができるかもしれません。このように、階層クラスター分析はデータ分析において強力な道具となるのです。
階層クラスター分析とは

階層クラスター分析は、多くのデータをいくつかの集団(クラスター)に分けるための統計的な手法です。この手法は、データ同士の似ている度合いを測り、似ているもの同士をまとめていくことで、データ全体の構造を把握することを目的としています。分析を行う際には、まず個々のデータがそれぞれ独立した集団として扱われます。そして、最も似ている二つの集団を一つにまとめて、新たな集団を作ります。この手順を繰り返し行うことで、最終的には全てのデータが一つの大きな集団に統合されます。
この一連のグループ化の過程は、樹形図と呼ばれる図で表現されます。樹形図は、木の枝のように階層的な構造を持っており、データ間の関係性を視覚的に理解するのに役立ちます。図の下の方では、個々のデータが小さな枝として表現され、上に行くほど枝が合わさり、最終的には一つの太い幹へと繋がります。枝の分岐点の高さを見ていくことで、どの集団がどれくらい似ているのかを判断することができます。分岐点が高いほど、二つの集団の類似度は低く、分岐点が低いほど、類似度は高いと言えます。
階層クラスター分析には、集団同士の似ている度合いを測る方法や、集団をまとめる方法など、様々な手法が存在します。その中でも、ウォード法はよく使われる手法の一つです。ウォード法は、集団をまとめる際に、集団内のばらつきが最小になるように工夫された手法です。ばらつきが小さい集団は、内部のデータ同士が似ている傾向があるため、より質の高い集団分けを行うことができます。階層クラスター分析は、マーケティング調査や生物学など、様々な分野で活用されています。
ウォード法の仕組み

ウォード法は、階層的なクラスター分析の手法の一つで、データの集合を似たもの同士で段階的にグループ化していく方法です。この手法の特徴は、グループを結合する際に、グループ内のばらつきの増加量を最小にするように最適化していく点にあります。
具体的には、まず全てのデータがそれぞれ一つのグループとして扱われます。次に、全てのグループのペアについて、それらを結合した場合にどれだけばらつきが増えるかを計算します。ばらつきとは、グループ内の各データと、そのグループの重心(平均値)との距離の二乗和で表されます。このばらつきの増加量が最も小さくなるグループのペアを選び、それらを結合して一つのグループにします。
この手順を繰り返すことで、最終的に全てのデータが一つの大きなグループになるまで結合を続けます。結合の過程は、樹形図と呼ばれる図で視覚的に表現できます。樹形図を見ると、どの段階でどのグループが結合されたのか、またグループ間の類似度がどの程度なのかを把握することができます。
ウォード法は、グループ内のばらつきを最小にすることを重視するため、大きさの均等なグループを作りやすい傾向があります。これは、他の階層クラスター分析の手法、例えば最短距離法や最長距離法などと比較した場合の大きな違いです。最短距離法や最長距離法は、グループ間の距離のみに基づいて結合を行うため、一つの大きなグループに次々とデータが吸収されていく、連鎖的な結合が起こりやすいという欠点があります。
ウォード法は、様々な分野で活用されています。例えば、マーケティングでは顧客をセグメント化するために、生物学では生物の分類を行うために用いられることがあります。ウォード法を用いることで、データの構造を理解し、より効果的な意思決定を行うための手助けとなります。
| 項目 | 内容 |
|---|---|
| 手法名 | ウォード法 |
| 種類 | 階層的クラスター分析 |
| 目的 | データの集合を似たもの同士で段階的にグループ化 |
| 特徴 | グループ結合時にばらつきの増加量を最小にするよう最適化 |
| ばらつき | グループ内の各データと重心(平均値)との距離の二乗和 |
| 手順 | 1. 全データを個別グループとして扱う 2. 全グループペアの結合によるばらつき増加量を計算 3. 増加量が最小のペアを結合 4. 全データが1グループになるまで繰り返す |
| 出力 | 樹形図(結合過程とグループ間類似度を視覚化) |
| 利点 | 大きさの均等なグループを作りやすい |
| 他手法との比較 | 最短・最長距離法は連鎖的な結合が起こりやすい |
| 応用分野 | マーケティング(顧客セグメント化)、生物学(生物分類)など |
ウォード法の利点

ウォード法は、異なる集団を段階的に結合していくことで分類を行う手法であり、その利点は多岐に渡ります。まず分類の精度が高いことが挙げられます。ウォード法は、集団をまとめる際に、集団内のばらつきが最小になるように結合を行います。ばらつきが小さい集団は、構成要素が互いに似通っていることを示すため、結果としてデータの特性をより正確に反映した集団分けが可能となります。これは他の分類手法と比較しても大きな強みです。
次に、樹形図によって視覚的にデータの構造を把握できる点も大きな利点です。ウォード法を用いると、どの集団がどの段階で結合されたのか、またその際にばらつきがどのように変化したのかを樹形図の形で表現できます。この樹形図を見ることで、データ全体の階層構造や集団間の関係性、データの類似度などを直感的に理解することが容易になります。データ分析において、視覚的な理解は非常に重要であり、複雑なデータの構造であっても、樹形図を用いることで容易に全体像を把握することが可能となります。
さらに、ウォード法は様々な種類のデータに適用できる汎用性の高さも魅力です。データの性質や尺度に大きな制約がなく、多様な分野のデータ分析に活用できます。例えば、市場調査における顧客の分類、生物学における種の分類、画像認識におけるパターンの分類など、応用範囲は非常に広いです。このように、精度の高さ、視覚的な分かりやすさ、そして汎用性の高さといった多くの利点を持つウォード法は、データ分析において強力な手法として幅広く活用されています。
| 利点 | 説明 |
|---|---|
| 分類の精度が高い | 集団内のばらつきが最小になるように結合するため、データの特性をより正確に反映した集団分けが可能。 |
| 視覚的な理解 | 樹形図によって、どの集団がどの段階で結合されたのか、ばらつきがどのように変化したのかを視覚的に把握できる。データ全体の階層構造や集団間の関係性、データの類似度を直感的に理解可能。 |
| 汎用性の高さ | データの性質や尺度に大きな制約がなく、多様な分野のデータ分析に活用できる。例:市場調査、生物学、画像認識など。 |
ウォード法の計算量

階層型クラスター分析の中で、ウォード法は計算に時間がかかる手法として知られています。他の手法、例えば、最短距離法や最長距離法などと比べると、ウォード法はデータ量の増加に伴い計算時間が急激に増える傾向があります。具体的には、扱うデータの数が増えると、計算時間は指数関数的に増加します。これは、ウォード法が、全てのクラスターの組み合わせを考慮して、クラスター間のばらつきが最小となるように併合していくためです。それぞれの併合ステップで、全ての組み合わせを評価する必要があるため、データの数が増えると計算量が爆発的に増えてしまうのです。
このような計算量の多さから、従来はウォード法を大規模なデータに適用することは困難でした。数万、数十万といったデータになると、計算が終わるまでに膨大な時間がかかってしまい、現実的ではありませんでした。しかし、近年ではコンピューターの処理能力が飛躍的に向上しています。それと同時に、ウォード法の計算アルゴリズムも改良されてきています。これらの進歩のおかげで、以前は不可能だった規模のデータに対しても、ウォード法を適用できるようになってきています。
計算に時間はかかりますが、ウォード法は精度の高い分類結果を期待できます。他の階層型クラスター分析の手法と比較すると、ウォード法はより均等な大きさのクラスターを作り出す傾向があります。これは、クラスター内のばらつきを最小にするという基準に基づいて併合を行うためです。そのため、データの構造をより正確に反映した分類結果を得られる可能性が高まります。ただし、計算時間と精度のバランスを考える必要があります。時間的な制約が厳しい場合や、データの規模が非常に大きい場合は、他の計算量の少ない手法を検討する方が良い場合もあります。状況に応じて、どの手法が適切なのかを見極めることが大切です。
| 手法 | 計算時間 | 特徴 | 利点 | 欠点 |
|---|---|---|---|---|
| ウォード法 | データ量の増加に伴い指数関数的に増加 | 全てのクラスターの組み合わせを考慮し、クラスター間のばらつきが最小となるように併合 | 精度の高い分類結果、均等な大きさのクラスター | 計算時間がかかる |
| 最短距離法、最長距離法など | ウォード法より計算時間が短い | – | 計算時間が短い | ウォード法より精度が低い可能性がある |
ウォード法の適用事例

ウォード法は、異なる集団をまとめる際に、集団内のばらつきが最小になるようにグループ分けを行う手法です。この手法は、様々な分野で活用され、データの背後にある隠れた構造や関係性を明らかにするのに役立っています。具体的にどのような分野でどのように活用されているのか、幾つかの事例を交えて見ていきましょう。
まず、販売戦略においては、顧客をいくつかの集団に分類するためにウォード法が用いられています。顧客の購買履歴や属性などのデータに基づいて集団分けを行うことで、それぞれの集団に合わせた販売促進活動を行うことが可能になります。例えば、ある商品を頻繁に購入する集団には、その商品の関連商品を勧めるといった具合です。このような顧客の集団分けは、効率的な販売促進活動につながり、売上向上に貢献します。
医療分野では、患者の症状や検査結果などのデータに基づいて、患者の類型化にウォード法が活用されています。例えば、ある病気の患者を症状の重さによって幾つかのグループに分け、それぞれのグループに最適な治療法を検討することができます。これにより、患者一人ひとりに合わせたより効果的な治療を提供することが期待されます。また、新しい病気の診断基準や治療法の開発にも役立つ可能性があります。
生物学の分野でもウォード法は活躍しています。遺伝子の働きに関するデータ分析にウォード法を適用することで、遺伝子の機能や相互作用の解明に役立っています。膨大な遺伝子データの中から関連性の高い遺伝子を見つけ出すことで、病気の原因究明や新薬開発に繋がることが期待されています。
このように、ウォード法は様々な分野で応用されており、データ分析を通じて新たな知見や発見をもたらしています。今後、データの蓄積が進むにつれて、ウォード法の活用範囲はますます広がり、様々な分野での発展に貢献していくと考えられます。
| 分野 | 活用例 | 効果 |
|---|---|---|
| 販売戦略 | 顧客の購買履歴や属性データに基づいた顧客の集団分け | 集団に合わせた販売促進活動、売上向上 |
| 医療 | 患者の症状や検査結果データに基づいた患者の類型化 | 患者に最適な治療法の検討、新薬開発 |
| 生物学 | 遺伝子の働きに関するデータ分析 | 遺伝子の機能や相互作用の解明、病気の原因究明 |
