ウォード法:データの集まりを作る賢い方法

AIを知りたい
先生、「ウォード法」って、たくさんのデータが集まっている時に使える便利な方法だっていうのはなんとなくわかったんですけど、具体的にどんな風に便利なんですか?

AIエンジニア
良い質問だね。たとえば、顧客をいくつかのグループに分けたいとしよう。ウォード法を使うと、顧客の購買履歴といったデータに基づいて、似たような行動をする顧客同士を自動的にグループ化してくれるんだ。

AIを知りたい
なるほど。でも、ただグループ分けするだけなら他の方法でもできそうですよね?ウォード法ならではの良さってなんでしょうか?

AIエンジニア
ウォード法は、グループ分けした後に、それぞれのグループの性質がはっきりと異なり、かつ、グループ内のばらつきが小さくなるようにしてくれる。つまり、より質の高いグループ分けができるんだ。だから、顧客への適切な広告配信や商品の推奨など、様々なマーケティング戦略に役立つんだよ。
ウォード法とは。
データの集まりをいくつかのグループに分ける方法の一つに、『ウォード法』というものがあります。この方法は、グループ分けしたときに、それぞれのグループ内のデータのばらつきが möglichst小さくなるように工夫されています。
まず、はじめの状態では、すべてのデータがそれぞれ独立したグループとして扱われます。そこから、グループ内のデータのばらつき(それぞれのデータの値と、グループ全体の平均値との差の二乗の合計)が最も小さくなるように、近いデータ同士をまとめて一つのグループにしていきます。
この作業を、あらかじめ決めておいたグループの数になるまで、あるいはすべてのデータを一つのグループにまとめるまで繰り返します。この方法は、比較的簡単な計算でグループ分けができるため、データがたくさんある場合に特に役立ちます。
ウォード法とは

ウォード法は、たくさんの情報から似た特徴を持つものの集まり(集団)を見つける方法です。階層的集団化と呼ばれる方法の一つで、情報の散らばり具合を最も小さくするように集団を作っていきます。
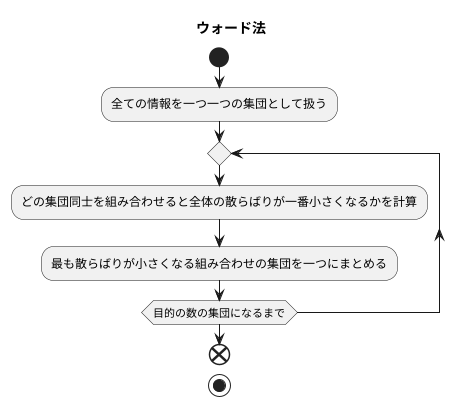
まず、全ての情報を一つ一つの集団として扱います。まるで、一人ひとりが独立した小さなグループのようですね。次に、どの集団同士を組み合わせると全体の散らばりが一番小さくなるかを計算します。例えば、東京都に住んでいる人、大阪府に住んでいる人、北海道に住んでいる人という三つの集団があったとします。東京都と大阪府の集団を組み合わせた場合の散らばり具合と、東京都と北海道の集団を組み合わせた場合の散らばり具合を計算し、より散らばりが小さくなる方を選びます。
最も散らばりが小さくなる組み合わせの集団を一つにまとめます。この手順を何度も繰り返すことで、最終的に目的の数の集団にまとめ上げます。三つの集団を一つにまとめることも、十個の集団を三つにまとめることも可能です。
ウォード法の特徴は、それぞれの段階で最も散らばりが小さくなるように集団を結合していくことです。そのため、似た性質の情報がきれいにまとまりやすいです。例えば、同じ趣味を持つ人々が自然と一つの集団になるように、データも似た者同士で集まるのです。
この方法は、情報の分布を図表などで分かりやすく把握しやすく、情報同士のつながりを理解するのに役立ちます。例えば、顧客の購買履歴を分析することで、どのような商品が一緒に買われているか、顧客の年齢や地域によってどのような購買傾向があるかを明らかにすることができます。このように、ウォード法は様々な分野で活用できる強力な情報分析手法と言えるでしょう。
散らばりを最小にする

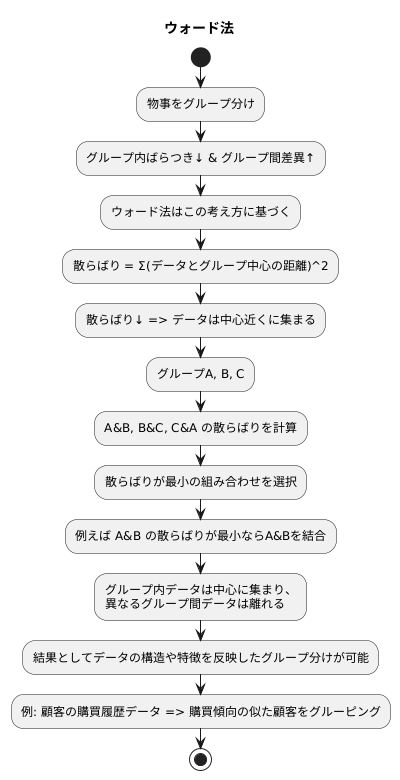
物事をいくつかのグループに分ける時、グループ内のばらつきを少なく、グループ同士の違いをはっきりさせることが重要です。ウォード法と呼ばれる方法は、まさにこの考え方に基づいてグループ分けを行います。「散らばり」とは、各データと所属するグループの中心との距離の二乗を合計した値で表されます。この値が小さいほど、データはグループの中心近くに集まっていることを示します。例えるなら、学校のクラスで、生徒たちが教室の真ん中に集まっているか、それとも教室の隅々に散らばっているかを測るようなものです。真ん中に集まっているほど、散らばりは小さくなります。
ウォード法では、二つのグループを一つにまとめる際に、この「散らばり」が最小になる組み合わせを選びます。例えば、A、B、Cという三つのグループがあったとします。AとBを合わせた場合の散らばり、BとCを合わせた場合の散らばり、CとAを合わせた場合の散らばりをそれぞれ計算し、最も散らばりが小さくなる組み合わせを選びます。もしAとBを合わせた場合の散らばりが最も小さければ、AとBを一つのグループにします。
このようにしてグループをまとめていくことで、各グループ内のデータはできるだけ中心に集まり、異なるグループ間のデータはできるだけ離れるように配置されます。これは、先ほどの学校のクラスの例で言えば、各クラスの生徒は教室の真ん中に集まっており、他のクラスの生徒とは教室が違うため、はっきりと区別できる状態です。
結果として、データの持つ本来の構造や特徴をうまく反映したグループ分けが可能になります。例えば、顧客の購買履歴データにウォード法を適用すれば、購買傾向の似た顧客を同じグループにまとめることができます。これは、より効果的な販売戦略を立てる上で役立ちます。
階層的クラスタリング

階層的クラスタリングは、データの集まりを類似性に基づいて階層構造で分類する手法です。まるで木が枝分かれするように、小さな集団が次第に大きな集団へと統合されていく様子を想像してみてください。この手法は、データの全体像を把握し、隠れた関係性を発見するのに役立ちます。
階層的クラスタリングは、最初は各データが一つの小さな集団を形成している状態から始まります。そして、最も似ている集団同士が段階的に結合されていきます。この結合のプロセスは、最終的にすべてのデータが一つの大きな集団になるまで、あるいはあらかじめ決めた集団の数になるまで続きます。
ウォード法はこの階層的クラスタリングの一種です。ウォード法は、集団を結合する際に、集団内のばらつきが最小になるように工夫されています。それぞれの集団は、できるだけ均質になるようにまとめられます。このため、ウォード法はデータの分類に偏りが少なく、正確な結果を得られることが期待されます。
階層的クラスタリングの利点の一つは、樹形図と呼ばれる図で結果を表せることです。樹形図は、データの階層構造を視覚的に表現したもので、どのデータがどの程度似ているかを一目で理解するのに役立ちます。また、集団の数を事前に決める必要がないことも利点です。樹形図を見ながら、データの特性に合った適切な集団の数を見つけることができます。これは、データの性質が事前にわからない場合に特に便利です。
このように、階層的クラスタリングは、データの関係性を理解し、柔軟な分類を行うための強力な手法と言えるでしょう。

大量データへの適用

ウォード法は、たくさんのデータに対しても有効に活用できる方法です。これは、計算方法が比較的簡単であることが理由です。データの集まりをいくつかのグループに分ける作業は、データの量が増えると計算が複雑になり、時間がかかるものもあります。しかし、ウォード法はデータが増えても計算時間の増加はそれほど大きくありません。つまり、大規模なデータ分析でも効率的にグループ分けを行うことができるのです。
例えば、お店の顧客の買い物データや、ホームページへのアクセス記録のような、たくさんのデータから顧客のグループ分けやホームページの利用状況を調べることができます。具体的には、顧客の買い物データから、よく似た商品を買う人のグループを見つけ、それぞれのグループに合わせたおすすめ商品を提示することで、売上向上につなげることができます。また、ホームページへのアクセス記録からは、どのページがよく見られているか、どのページから他のページへ移動しているかなどを分析し、ホームページの構成を改善することで、より使いやすくすることができます。
ウォード法を使うことで、たくさんのデータの中に隠れている規則性や関係性を見つけることができます。例えば、ある商品をよく買う人は、別の特定の商品もよく買うといった関係性や、特定の年齢層の顧客がよくアクセスするページといった規則性を見つけ出すことが可能です。これらの発見は、商品の仕入れ計画や販売戦略、ホームページのデザイン改善といった、事業の意思決定に役立てることができます。ウォード法は、データの量に左右されずに安定した結果を得られるため、信頼性の高い分析手法として、幅広い分野で活用されています。
| 項目 | 説明 |
|---|---|
| 手法名 | ウォード法 |
| 特徴 | 大規模データにも効率的に適用可能、計算が比較的簡単 |
| メリット | データ量の増加による計算時間の増加が少ない、安定した結果を得られる、信頼性が高い |
| 用途 | 顧客のグループ分け、ホームページの利用状況分析、商品の仕入れ計画、販売戦略、ホームページのデザイン改善 |
| 適用例1 | 顧客の買い物データからよく似た商品を買う人のグループを見つけ、おすすめ商品を提示 |
| 適用例2 | ホームページへのアクセス記録から、よく見られているページやページ間の移動を分析し、構成を改善 |
| 効果 | 売上向上、ホームページの使いやすさの向上、事業の意思決定支援 |
他の手法との比較

データの集まりをいくつかのグループに分ける方法、つまりクラスタリングには、様々なやり方があります。その中で、よく知られているものにウォード法とK平均法があります。これらの二つの方法を比べてみましょう。
K平均法では、最初にいくつのグループに分けるかを決めておく必要があります。そして、それぞれのグループの中心点を適当に決めます。次に、データの一つ一つを見て、どのグループの中心点に近いかによってグループ分けをします。グループ分けが終わったら、それぞれの中心点をグループの中のデータの平均の位置に移動させます。この作業を、中心点がほとんど動かなくなるまで繰り返します。このように、あらかじめグループの数を決めておく必要があることと、最初の中心点の決め方によって結果が変わってしまうことがK平均法の弱点です。
一方、ウォード法では、階層的にグループを作っていきます。最初は、それぞれのデータが一つのグループだと考えます。次に、最も似ている二つのグループをくっつけて一つのグループにします。これを繰り返していくと、最終的に全てのデータが一つのグループになります。その過程で、どの段階でグループ分けを止めるかによって、グループの数を調整できます。K平均法のように最初の中心点を決める必要がないため、結果が安定しているという利点があります。
また、K平均法は丸い形のグループを作りやすいという特徴があります。これは、中心点からの距離でグループ分けをするためです。一方、ウォード法は様々な形のグループを作ることができます。
どの方法を使うのが良いかは、データの形や分析の目的によって異なります。データが丸い形に集まっている場合はK平均法が適しているかもしれません。しかし、データの形が複雑な場合やグループの中にさらに小さなグループがあるような階層構造を調べたい場合は、ウォード法の方が良い結果を得られるでしょう。
| 項目 | K平均法 | ウォード法 |
|---|---|---|
| グループ数 | あらかじめ決める必要がある | 階層的にグループを作成し、どの段階で止めるかで調整可能 |
| 初期値 | 中心点を最初に決める必要があるため、結果が初期値に依存する | 初期値の設定が不要で、結果が安定している |
| グループの形 | 丸い形のグループを作りやすい | 様々な形のグループを作ることができる |
| 適したデータ | データが丸い形に集まっている場合 | データの形が複雑な場合や階層構造を持つデータ |
まとめ

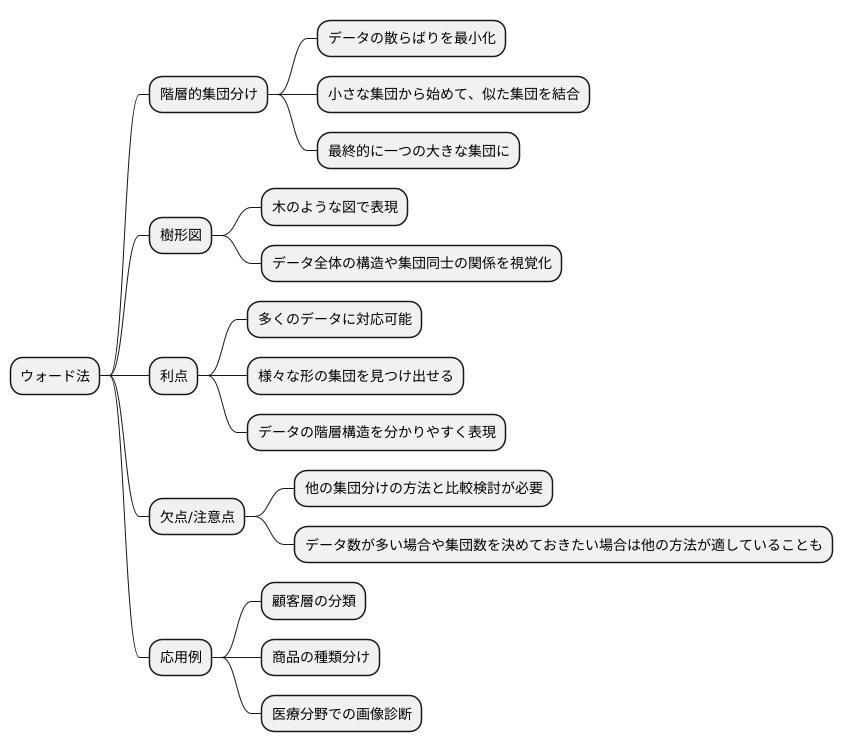
まとめとして、ウォード法はデータの散らばりを最小にすることを目指す、階層的な集団分けの方法です。階層的とは、集団を段階的にまとめていくことを意味します。小さな集団から始めて、似た集団同士を順次結合し、最終的に一つの大きな集団になるまで繰り返します。この過程は、まるで木が枝分かれしていくように図示化され、これを樹形図と呼びます。樹形図を見ることで、データ全体の構造や集団同士の関係が視覚的に理解できます。
ウォード法の利点は、多くのデータにも対応できる点と、様々な形の集団を見つけ出せる点です。丸い形だけでなく、複雑な形の集団にも対応できるため、データの特性に合わせて柔軟に適用できます。また、樹形図によってデータの階層構造が分かりやすく表現されるため、データ全体を把握しやすくなります。
ただし、ウォード法は他の集団分けの方法と比較検討した上で、データの性質や分析の目的に合ったものを選ぶことが大切です。例えば、データの数が非常に多い場合や、あらかじめ集団の数を決めておきたい場合は、他の方法が適していることもあります。
ウォード法は、様々な分野で活用されています。例えば、販売促進のための顧客層の分類や、膨大な商品の種類分け、医療分野での画像診断など、応用範囲は多岐に渡ります。データに隠された規則性や構造を見つけ出し、新たな発見に繋がる強力な分析手法と言えるでしょう。