ウォード法:データの分類手法

AIを知りたい
先生、「ウォード法」って、データがいっぱいあるときに役立つって書いてあるけど、どうしてそうなの?

AIエンジニア
いい質問だね。ウォード法は、計算が比較的簡単だから、たくさんのデータがあってもあまり時間がかからないんだ。他の複雑な方法だと、データが多いと計算にすごく時間がかかってしまうことがあるからね。

AIを知りたい
なるほど。計算が簡単なのは、具体的にどういうこと?

AIエンジニア
ウォード法では、どのデータをまとめるかを決めるのに、グループ全体でどれくらいデータがばらついているか、っていうのを計算する。この計算が比較的単純で、コンピュータでも速く処理できるんだ。だからデータが多いときにも使いやすいんだよ。
ウォード法とは。
データの集まりを似た者同士でまとめていく方法の一つに『ウォード法』というものがあります。この方法は、データがバラバラに散らばる程度をできるだけ小さくするようにグループ分けしていくやり方です。はじめは、それぞれのデータが全部別々のグループとして扱われます。そこから、データ同士の散らばりが一番小さくなるように、似たデータを集めて一つのグループにしていきます。この作業を、あらかじめ決めておいたグループの数になるまで、あるいは全てのデータが一つの大きなグループになるまで繰り返します。この方法は簡単に計算できるので、たくさんのデータがあるときに役立ちます。
はじめに

近頃では、あらゆる分野で情報の集まりを扱うことが欠かせなくなってきています。集めた情報の中から価値あるものを探し出し、それを基に次の行動を決めるということが、仕事でも研究でも必要とされているのです。このような状況の中で、情報の集まりを扱う技術の中でも、特に「集まり分け」という手法が重要になってきています。「集まり分け」とは、情報同士がどれくらい似ているかを基準にして、情報の集まりをいくつかのグループに分ける方法です。この方法を使うことで、情報の集まりの構造や隠れた規則性を見つけることができるのです。
情報の集まりをいくつかのグループに分ける方法はたくさんありますが、今回はその中でも「寄り合い分け」と呼ばれる方法について詳しく説明します。「寄り合い分け」は、グループ同士の似ている度合いを測る方法の一つで、グループ内の情報のばらつきが小さいほど、グループ同士が似ていると判断します。具体的には、それぞれのグループの中の情報が、そのグループの中心からどれくらい離れているかを計算し、その平均値を「ばらつき」として扱います。そして、グループ同士をくっつけて新しいグループを作ったときに、この「ばらつき」がどれくらい増えるかを計算します。「ばらつき」の増え方が小さいグループ同士から順番にくっつけていくことで、最終的に最適なグループ分けを行うことができるのです。
「寄り合い分け」は、グループ内の情報のばらつきを最小にするという明確な基準に基づいているため、結果の解釈がしやすいという利点があります。また、計算方法も比較的単純であるため、大規模な情報の集まりにも適用しやすいという特徴があります。しかし、あらかじめグループの数を決めておく必要があるため、適切なグループ数が分からない場合には、試行錯誤が必要となる場合があります。さらに、データの種類によっては、適切なグループ分けができない場合もあるため、注意が必要です。
このように、「寄り合い分け」は情報の集まりを扱う上で非常に強力な手法ですが、その特性を理解した上で適切に利用することが重要です。今後、様々な場面で「寄り合い分け」を活用していくために、まずは基本的な考え方と計算方法をしっかりと理解しておきましょう。
| 手法 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| 集まり分け | 情報同士の類似度を基準に、情報の集まりをいくつかのグループに分ける方法。情報の集まりの構造や隠れた規則性を見つけることができる。 | ||
| 寄り合い分け | グループ内の情報のばらつきが小さいほど、グループ同士が似ていると判断する「集まり分け」の一種。グループ内の情報の中心からの距離の平均値を「ばらつき」として、ばらつきの増え方が小さいグループ同士からくっつけていく。 |
|
|
ウォード法とは

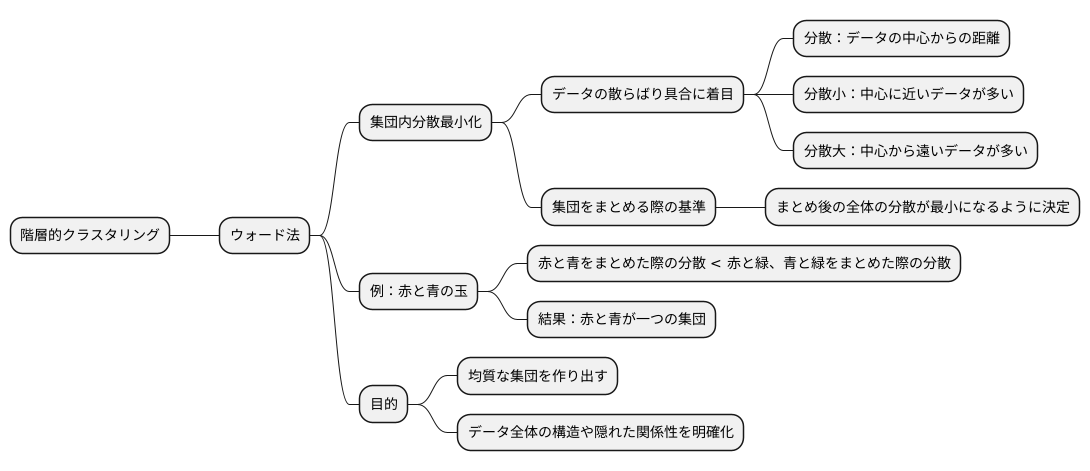
ウォード法は、階層的クラスタリングという手法を用いた分析方法の一つです。階層的クラスタリングとは、まるで木が枝分かれしていくように、データを小さな集団から徐々に大きな集団へとまとめていく方法です。データ同士の繋がりを段階的に明らかにしていくことで、最終的に階層構造を持った集団、つまりクラスタを形成します。
様々な階層的クラスタリングの手法の中でも、ウォード法は集団内のデータの散らばり具合、すなわち分散に着目します。分散とは、データが中心からどれくらい離れているかを表す指標です。中心に近いデータが多いほど分散は小さく、中心から遠いデータが多いほど分散は大きくなります。ウォード法では、二つの集団を一つにまとめる際、まとめた後の集団全体の分散が最小になるように、どの集団同士をまとめるかを決定します。
例えば、赤い玉の集団と青い玉の集団があるとします。ウォード法では、この二つの集団を一つにまとめた際に、赤と青の玉がなるべく狭い範囲に収まるように、つまり分散が小さくなるようにまとめます。もし近くに緑の玉の集団があったとしても、赤と青の玉をまとめた時よりも、赤と緑、あるいは青と緑の玉をまとめた時の方が分散が大きくなる場合は、赤と青の玉が一つの集団として扱われます。
このように、ウォード法は集団内のばらつきを最小限にすることで、似た性質を持つデータ同士を的確にまとめ、より均質な集団を作り出すことを目指します。結果として、データ全体の構造や隠れた関係性をより明確に理解することが可能になります。
計算の手順

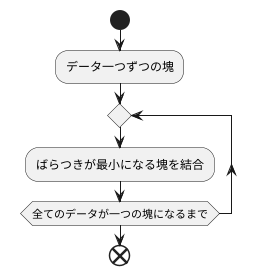
計算の手順を具体的に見ていきましょう。まず、全てのデータを一つずつの塊として考えます。それぞれの塊にはデータが一つだけ入っている状態です。これが最初の状態です。次に、これらの塊をどのようにまとめていくかを考えます。塊同士を繋げることで、より大きな塊を作っていくのです。
どの塊とどの塊を繋げるかを決めるために、塊を繋げた時に増えるばらつきを調べます。ばらつきとは、データの散らばり具合のことです。例えば、同じような値のデータが集まっている場合はばらつきが小さく、様々な値のデータが混ざっている場合はばらつきが大きくなります。
ばらつきが最も小さくなるように塊を繋げることで、似たデータ同士をまとめていくことができます。この手順を繰り返すことで、階層構造を持った塊が作られます。最初はデータが一つずつバラバラに入っていた小さな塊が、徐々に大きな塊へと成長していく様子を思い浮かべてみてください。
この作業を全てのデータが一つの大きな塊になるまで続けるのが基本的な手順です。ただし、場合によっては、あらかじめ決めておいた数の塊になるまで続けることもあります。例えば、三つの塊に分けたい場合は、塊の数が三つになるまで繋げる作業を繰り返します。このようにして、ウォード法では似たデータ同士をまとめていくことで、データ全体の構造を明らかにしていきます。
利点と欠点

ウォード法は、大量の情報を扱う際に役立つ手法であり、複数の情報のかたまりを形成する際に用いられます。この手法には、良い点と悪い点の両方が存在します。まず、良い点としては、計算の手間が比較的少ないことが挙げられます。多くの情報を扱う場合でも、効率的に処理することができるため、時間と労力を節約できます。また、情報のかたまりのばらつき具合を基準に形成するため、結果としてできるかたまりの中の情報は互いに似たものになる傾向があります。これは、かたまりごとの特徴がはっきりし、分析結果を理解しやすくなることを意味します。
一方で、ウォード法には注意すべき点もいくつかあります。大きな欠点として、一度情報のかたまりをくっつけてしまうと、それを取り消すことができない点が挙げられます。くっつける順番を間違えると、最終的な結果に大きな影響を与えてしまう可能性があります。例えば、本来別々のかたまりに属するべき情報がくっついてしまうと、分析結果の正確性が損なわれます。また、ウォード法は、全てのかたまりが同じくらいの大きさになることを前提としているため、大きさの異なるかたまりが混在するデータには不向きです。このようなデータにウォード法を適用すると、適切なかたまりの形成が難しくなり、誤った結果が導き出される可能性があります。
そのため、ウォード法を用いる際には、データの特性を十分に理解し、適切なかたまりの数を設定することが非常に重要です。情報のかたまりの数を事前に決める必要がありますが、その数を適切に設定しないと、結果の解釈が難しくなります。もし、かたまりが多すぎると、それぞれの特徴が不明瞭になり、全体像の把握が困難になります。逆に、かたまりが少なすぎると、重要な情報が見落とされる可能性があります。このように、ウォード法は強力な手法ですが、その特性を理解し、適切に利用することが重要です。
| 項目 | 内容 |
|---|---|
| 良い点 | – 計算の手間が少ない – かたまり内の情報は互いに似たものになる傾向がある |
| 悪い点 | – 一度くっつけたかたまりは取り消せない – 全てのかたまりが同じくらいの大きさになることを前提としている – かたまりの数を事前に決定する必要がある |
| 注意点 | – データの特性を理解する – 適切なかたまりの数を設定する |
応用例

ウォード法は、多様な分野で活用されている、データ分析の手法です。その応用範囲の広さから、多くの事例が見られます。具体的にどのような場面で役立っているのか、いくつか見ていきましょう。まず、事業の場では、顧客をいくつかの集団に分類するために使われています。例えば、顧客の購買履歴や商品の閲覧履歴といったデータから、顧客の行動パターンを見つけ出し、似た行動をする顧客同士をまとめていくことで、顧客層を明確にすることができます。それぞれの顧客層に合わせた販売戦略を立てることで、より効果的な販売促進活動を行うことができます。
次に、生き物の研究分野でも、ウォード法は活用されています。細胞の種類を判別するために、遺伝子の働き方のデータを用いて細胞を分類します。似た働き方をする遺伝子を持つ細胞をグループ化することで、細胞の種類や役割を理解することができます。この手法は、病気の仕組みを解明したり、新しい治療法を開発したりする上で重要な役割を果たしています。
さらに、画像を扱う分野でも、ウォード法は力を発揮します。画像認識技術において、画像の特徴を捉え、似た特徴を持つ画像をまとめてグループ分けすることで、画像の分類や整理を行うことができます。大量の画像データを扱う際に、ウォード法を用いることで、効率的に画像を管理し、必要な情報を取り出すことができます。
このように、ウォード法は、データの構造を把握し、隠れた関係性を見つけ出すための強力な道具です。データの種類や分析の目的に合わせて適切に使うことで、様々な分野で有益な知見を得ることができ、新たな発見につながる可能性を秘めています。 ウォード法は、これからも様々な分野で応用され、発展していくことが期待される手法です。
| 分野 | 活用例 | データ例 | 目的 |
|---|---|---|---|
| 事業 | 顧客の分類 | 購買履歴、商品の閲覧履歴 | 顧客層を明確化し、効果的な販売戦略を立てる |
| 生き物の研究 | 細胞の種類の判別 | 遺伝子の働き方のデータ | 細胞の種類や役割の理解、病気の仕組みの解明、新しい治療法の開発 |
| 画像処理 | 画像の分類・整理 | 画像の特徴データ | 効率的な画像管理、必要な情報の抽出 |
まとめ

まとめとして、ウォード法はデータの集まりをいくつかのグループ(かたまり)に分ける手法であり、その分け方には明確なルールがあります。具体的には、グループ分けの際に、それぞれのグループ内のデータのばらつきが最小になるように工夫されています。これは、同じグループに属するデータは互いに似ているべきという考え方に基づいています。
この手法の大きな利点は、計算の手間が比較的少ないことです。そのため、たくさんのデータでも速やかに処理できます。また、出来上がるグループはそれぞれ中身が似通っており、グループの特徴をつかみやすいという良さもあります。例えば、顧客を購買行動に基づいてグループ分けする場合、ウォード法を用いることで、似たような購買行動をする顧客をまとめてグループ化し、それぞれのグループに適した販売戦略を立てることができます。
しかし、ウォード法には、一度グループをまとめてしまうと、後から分割できないという弱点もあります。例えば、一度「果物」と「野菜」をまとめて「農産物」というグループにしてしまうと、後から「果物」と「野菜」を別々のグループとして扱うことはできません。このように、一度行ったグループ分けは取り消せないため、最初のグループ分けを慎重に行う必要があります。具体的には、データの性質をよく理解し、適切なグループ数を決めることが重要です。
ウォード法は、販売戦略の立案や生物の分類など、様々な分野で広く使われています。データに隠された構造を明らかにし、新しい発見に繋がるウォード法は、これからも様々な分野で役立つ手法と言えるでしょう。
| 項目 | 内容 |
|---|---|
| 手法名 | ウォード法 |
| 目的 | データの集まりをいくつかのグループ(かたまり)に分ける |
| ルール | グループ内のデータのばらつきが最小になるようにグループ分け |
| 利点 | 計算の手間が少なく、大量データの処理に適している グループの特徴をつかみやすい |
| 例 | 顧客を購買行動に基づいてグループ分けし、販売戦略を立てる |
| 欠点 | 一度グループをまとめると、後から分割できない |
| 注意点 | データの性質をよく理解し、適切なグループ数を決める |
| 応用例 | 販売戦略の立案、生物の分類など |
