様々なサンプリング手法

AIを知りたい
『サンプリング手法』って、たくさんのデータから一部を取り出す方法ですよね?でも、どうして色々な種類があるんですか?

AIエンジニア
そうだね、一部を取り出す方法で合ってるよ。色々な種類があるのは、データの性質や、取り出したいデータの特徴によって、最適な方法が違うからなんだ。たとえば、くじ引きのように、全部が同じ確率で選ばれるようにしたい場合と、偏りがあるデータから、その偏りを反映した一部を取り出したい場合では、使う方法が変わるよね。

AIを知りたい
なるほど。じゃあ、偏りがあるデータから、その偏りを反映した一部を取り出す方法ってどんなものがありますか?

AIエンジニア
例えば、マルコフ連鎖モンテカルロ法っていうのがあるよ。これは、複雑な確率分布を持つデータから、その分布に合った形でデータを取り出すことができるんだ。他にも、逆関数法など、色々な方法があるよ。
サンプリング手法とは。
人工知能でよく使われる『抽出方法』について説明します。抽出方法とは、たくさんのデータが集まったものから、一部のデータを取り出す方法のことです。データの集まり方には、均等に散らばっているものや、中心に集まっているものなど、様々な種類があります。人工知能が新しいデータを作る場合は、もとになったデータの散らばり方を学習し、それと似たような散らばり方になるように新しいデータを作ります。抽出方法には、マルコフ連鎖モンテカルロ法や逆関数法など色々な種類があり、どの方法を使うかによって、作られるデータも変わってきます。
サンプリング手法とは

統計や機械学習といった分野では、膨大な量の情報を扱うことがしばしばあります。これらの情報を全て調べるのは、時間や費用がかかりすぎるため、現実的ではありません。そこで、全体の性質をできる限り反映した一部の情報だけを取り出して、全体の様子を推測するという方法がよく用いられます。この手法を、サンプリング手法といいます。
全ての情報を集めたものを母集団、母集団から取り出した一部の情報を標本といいます。たとえば、ある池にいる魚全ての数を調べたいとします。池の水を全て抜いて魚を数えるのは大変な作業です。そこで、網を使って魚を何匹か捕まえ、その捕まえた魚の数を基に、池にいる魚全体の数を推測することができます。この場合、池にいる魚全てが母集団、網で捕まえた魚が標本にあたります。
サンプリング手法は、母集団の特徴を正しく捉えた標本を得るための様々な方法です。例えば、無作為抽出という手法では、母集団から偏りなく標本を選び出します。これは、くじ引きのように、どの情報も等しい確率で選ばれるようにする方法です。一方、層化抽出という手法では、母集団をいくつかのグループに分け、それぞれのグループから標本を抽出します。これは、例えば、年齢層別にグループ分けして、各年齢層から標本を抽出するような場合に用いられます。
適切なサンプリング手法を選ぶことは、母集団の性質を正しく推測するために非常に重要です。もし、標本が母集団の特徴を正しく反映していなければ、得られる推測結果も不正確なものになってしまいます。機械学習の分野では、学習に用いるデータを選んだり、データを新しく作る際に、サンプリング手法が欠かせないものとなっています。
| 用語 | 説明 | 例 |
|---|---|---|
| 母集団 | 調査対象の全体 | 池にいる魚全て |
| 標本 | 母集団から取り出した一部の情報 | 網で捕まえた魚 |
| サンプリング手法 | 母集団の特徴を正しく捉えた標本を得るための方法 | 無作為抽出、層化抽出 |
| 無作為抽出 | 母集団から偏りなく標本を選び出す方法 | くじ引き |
| 層化抽出 | 母集団をいくつかのグループに分け、それぞれのグループから標本を抽出する方法 | 年齢層別にグループ分けして、各年齢層から標本を抽出 |
確率分布からのサンプリング

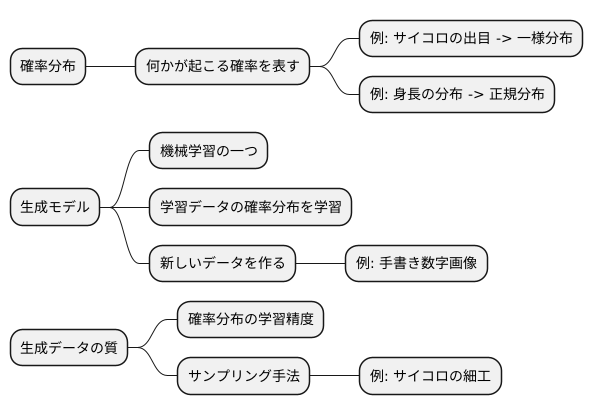
物事の起こりやすさを表すものとして、確率分布というものがあります。確率分布とは、ある出来事がどれくらいの確率で起こるかを示す数式のようなものです。例えば、正しく作られたサイコロを振ると、どの目も1/6の確率で出るため、これは一様分布と呼ばれる確率分布で表されます。また、多くの人の身長の分布は、平均値付近に人が集まり、平均から離れるほど人数が少なくなる釣鐘型の分布になり、これは正規分布という確率分布で近似できます。
近年の機械学習の分野では、学習したデータと同じような新しいデータを作る生成モデルというものが注目されています。この生成モデルは、学習データがどのような確率分布に従っているかを学習し、その学習した確率分布を使って新しいデータを作るのです。例えば、沢山の手書き数字の画像を学習データとして与えると、生成モデルは手書き数字の画像の分布を学習します。そして、学習した分布に基づいて、新しい手書き数字の画像を生成することができるようになります。
生成モデルで生成されるデータの質は、確率分布をどれだけ正確に学習できたかと、学習した確率分布からどのようにデータをサンプリングするかの2つの点に大きく左右されます。確率分布の学習が不十分だと、生成されるデータが学習データと全く異なるものになってしまう可能性があります。また、たとえ確率分布の学習が完璧であったとしても、サンプリングのやり方がまずければ、やはり生成データの質は悪くなってしまいます。例えば、サイコロを振る場合、特定の目が出るように細工されていると、本来の一様分布から得られるデータとは異なるデータが得られてしまいます。同様に、生成モデルにおいても、より良いサンプリング手法を用いることで、学習データに近い、質の高いデータを生成することが可能になるのです。
代表的なサンプリング手法

調べたい集団全体から一部を取り出して調べる方法を、標本調査と言います。この調査方法で大切なのは、どのように一部を取り出すかということです。取り出し方を工夫することで、全体の特徴を正しく反映した結果を得ることができます。この取り出し方をサンプリング手法と言い、いくつかの種類があります。
まず、単純無作為抽出法は、くじ引きのように、どの要素にも同じ確率で選ばれる機会が与えられる方法です。例えば、壺の中にたくさんの玉が入っていて、そこから目隠しをしていくつか取り出す様子を想像してみてください。この方法は、調べたい集団全体の特徴がほぼ同じである場合に適しています。
次に、層化抽出法は、調べたい集団をいくつかのグループに分けて、それぞれのグループから一部を取り出す方法です。例えば、男女比や年齢層など、あらかじめグループ分けしたうえで、各グループから同じ割合で取り出します。これは、調べたい集団全体が、異なる特徴を持つグループで構成されている場合に適しています。全体の特徴を正しく反映するためには、グループ分けが重要です。
最後に、集落抽出法は、調べたい集団をいくつかの集まりに分けて、その中からいくつかを選び、選ばれた集まりに属するものをすべて調べる方法です。例えば、学校をいくつかの地区に分けて、その中からいくつかの地区を選び、選ばれた地区のすべての学校を調べる様子を想像してみてください。この方法は、調べたい集団全体に多くの集まりがあり、それぞれの集まりの特徴が似ている場合に、費用や時間を節約できるという利点があります。
どのサンプリング手法を選ぶかは、調べたい集団の特徴や、調査の目的、使える費用や時間などを考えて決めることが大切です。
| サンプリング手法 | 説明 | 例 | 適切な状況 |
|---|---|---|---|
| 単純無作為抽出法 | どの要素にも同じ確率で選ばれる機会が与えられる方法 | 壺の中から目隠しをして玉を取り出す | 調べたい集団全体の特徴がほぼ同じである場合 |
| 層化抽出法 | 調べたい集団をいくつかのグループに分けて、それぞれのグループから一部を取り出す方法 | 男女比や年齢層など、あらかじめグループ分けしたうえで、各グループから同じ割合で取り出す | 調べたい集団全体が、異なる特徴を持つグループで構成されている場合 |
| 集落抽出法 | 調べたい集団をいくつかの集まりに分けて、その中からいくつかを選び、選ばれた集まりに属するものをすべて調べる方法 | いくつかの地区に分けた学校から、いくつかを選び、選ばれた地区のすべての学校を調べる | 調べたい集団全体に多くの集まりがあり、それぞれの集まりの特徴が似ている場合。費用や時間を節約できる。 |
機械学習におけるサンプリング手法

計算機を使って学ぶ仕組みの中でも、見本を選ぶやり方はとても大切です。色々な見本を選ぶやり方があり、それぞれに特徴があります。ここでは代表的なやり方をいくつか詳しく見ていきましょう。まず、マルコフ連鎖モンテカルロ法は、鎖のようにつながった一連の見本を作り出す方法です。前の見本の情報をもとに次の見本を作り、これを繰り返すことで、複雑な分布からでも見本を集めることができます。まるで鎖が目的の場所にたどり着くように、徐々に望みの分布に近づいていくのです。この方法は、特に形が複雑で捉えにくい分布を扱う時に役立ちます。次に、逆関数法は、一様分布という、どの値も同じ確率で現れる分布を利用します。この一様分布から作った見本を、目的の分布の形に合わせて変形することで、望みの分布に従う見本を作り出します。言ってみれば、型に合わせて材料を切り抜くような方法で、比較的簡単な分布から複雑な分布の見本を作ることができます。そして、棄却サンプリングは、別の分布を使って見本を作り、それを基準に従って選別する方法です。まず、簡単に作れる別の分布から見本をたくさん作ります。次に、作った見本が目的の分布に合うかどうかを調べ、合わないものは捨てます。残った見本は目的の分布の特徴をよく表しているので、これを使うことで複雑な分布の見本を得ることができるのです。これは、ふるいにかけて必要なものだけを残すようなイメージです。これらの方法は、それぞれに得意な分布や計算の手間などが違います。そのため、扱う問題によって最適な方法を選ぶことが重要になります。最近は、深層学習と呼ばれる、人間の脳をまねた仕組みを使った新しい見本を選ぶ方法も研究されています。この方法は、より複雑なデータを作ることを可能にし、今後の発展が期待されています。
| 手法名 | 説明 | 特徴 | イメージ |
|---|---|---|---|
| マルコフ連鎖モンテカルロ法 | 前の見本の情報をもとに次の見本を作り、鎖のように繋げることで目的の分布からの見本を得る方法。 | 複雑な分布を扱うのに適している。 | 鎖が目的の場所にたどり着くように、徐々に望みの分布に近づく。 |
| 逆関数法 | 一様分布から作った見本を、目的の分布の形に合わせて変形することで見本を得る方法。 | 比較的簡単な分布から複雑な分布の見本を作ることができる。 | 型に合わせて材料を切り抜く。 |
| 棄却サンプリング | 別の分布から見本を作り、それを基準に従って選別することで見本を得る方法。 | 複雑な分布の見本を得ることができる。 | ふるいにかけて必要なものだけを残す。 |
| 深層学習 | 人間の脳をまねた仕組みを使った新しい見本を選ぶ方法。 | より複雑なデータを作ることを可能にする。今後の発展が期待される。 | (記載なし) |
サンプリング手法の選択

調査や研究を行う上で、母集団全体を調べることは時間や費用がかかりすぎるため、母集団から一部を抜き取って調べるサンプリングという手法がよく用いられます。どのサンプリング手法を選ぶかは、調査の目的や得られる結果の正確さに大きく影響するため、慎重に検討する必要があります。
まず、母集団の特徴を把握することが重要です。母集団の大きさが比較的小さく、全ての要素を調べることが容易な場合は、全数調査が可能です。しかし、大規模な母集団の場合は、サンプリングが不可欠となります。母集団の構成要素に偏りがある場合は、その偏りを考慮したサンプリング手法を選ぶ必要があります。例えば、特定の属性を持つ要素が多く存在する場合、それらを適切な割合で含めるように工夫する必要があります。
次に、利用できる資源も考慮しなければなりません。限られた時間や費用の中で調査を行う必要がある場合、計算に時間のかからない単純なサンプリング手法を選ぶ方が良いでしょう。また、使える人材や機材も制限要因となるため、それらに見合った手法を選択する必要があります。
さらに、どの程度の正確さが必要かも重要な判断基準です。高い精度を求める場合は、より複雑で高度なサンプリング手法を用いる必要があります。ただし、精度の向上は計算量の増加を伴うため、費用や時間とのバランスを考える必要があります。例えば、許容できる誤差範囲をあらかじめ設定し、それを満たす範囲でなるべく簡素な手法を選択することで、効率的な調査を実現できるでしょう。
目的に最適なサンプリング手法を選択することで、限られた資源を有効活用しながら、信頼性の高い結果を得ることが可能になります。調査の計画段階で、これらの要素を十分に検討し、最適な手法を選び出すことが、調査全体の成功を左右すると言えるでしょう。
| 考慮事項 | 詳細 | 対応 |
|---|---|---|
| 母集団の特徴 |
|
|
| 利用できる資源 |
|
資源に見合った手法を選択 |
| 必要な正確さ | 許容できる誤差範囲 |
|
