予測精度指標RMSPEを理解する

AIを知りたい
先生、「RMSPE」(機械学習における平均二乗パーセント誤差の平方根)って、何ですか?よくわからないです。

AIエンジニア
そうですね。「RMSPE」は予測の正確さを評価する尺度の一つです。たとえば、来月の商品の売り上げ個数を予測したとします。実際の売り上げ個数と予測した売り上げ個数の差が小さいほど、予測の精度は高いですよね。この差をパーセントで表し、その平均を計算して平方根をとったものがRMSPEです。

AIを知りたい
パーセントで表すというのは、実際の売り上げ個数に対する誤差の割合ということですか?

AIエンジニア
その通りです。割合を使うことで、異なる規模の予測でも比較しやすくなります。例えば、100個売れるものを10個多く予測するのと、1000個売れるものを100個多く予測するのは、同じ10%の誤差ということになります。RMSPEは誤差の割合をベースにしているので、こうした比較を可能にするのです。
RMSPEとは。
人工知能の分野で使われる言葉、『RMSPE』(機械学習でよく使われる、予測の誤差の大きさをパーセントで表し、その二乗平均の平方根をとったもの)について説明します。
はじめに

機械学習のモデルを評価することは、どのモデルを選ぶか、また、どう改良していくかを決める上でとても大切です。適切な評価の尺度を使うことで、モデルの長所と短所を理解し、より正確な予測ができるモデルを作ることができます。たくさんの評価尺度の中でも、平均二乗パーセント誤差の平方根(RMSPE)は、予測値と実際の値の差を比率で捉えることができるため、特に商品の需要予測や売上の予測といったビジネスの場面で広く使われています。
このRMSPEは、誤差をパーセントで表すため、異なる規模のデータでも比較しやすいという長所があります。たとえば、値段の高い商品と値段の低い商品の売上予測を比較する場合、誤差の絶対値を見るRMSEのような尺度を使うと、値段の高い商品の誤差が大きく見えてしまうことがあります。しかし、RMSPEを使うことで、それぞれの商品の売上に対する誤差の比率を評価できるため、より公平な比較ができます。
RMSPEの計算は、まずそれぞれのデータについて、実際の値と予測値の差を実際の値で割ります。これを二乗し、全てのデータで平均を取った後、平方根を求めます。この計算方法により、パーセント単位での誤差が平均的にどのくらいかを把握できます。
他の指標と比較すると、RMSPEは相対的な誤差を見るため、RMSEのように絶対的な誤差を見る指標とは使い分けが必要です。RMSEは全体の誤差の大きさを捉えるのに適していますが、データの規模に影響を受けやすいという欠点があります。一方、RMSPEは規模の影響を受けにくいですが、実際の値がゼロに近い場合、計算が不安定になる可能性があります。
RMSPEは様々な場面で活用されています。例えば、小売業では商品の需要予測に、製造業では生産量の調整に、金融業界では株価の予測などに利用されています。これらの事例からも、RMSPEが実用的な指標であることが分かります。本稿では、これからRMSPEの計算方法や他の指標との比較、そして実際の活用事例を通じて、その有用性を詳しく説明していきます。
| 評価尺度 | 説明 | 長所 | 短所 | 使用例 |
|---|---|---|---|---|
| RMSPE (平均二乗パーセント誤差の平方根) | 予測値と実際の値の差を比率で捉える | 異なる規模のデータでも比較しやすい | 実際の値がゼロに近い場合、計算が不安定になる可能性がある | 商品の需要予測、売上の予測、株価の予測 |
| RMSE (平均二乗誤差の平方根) | 全体の誤差の大きさを捉える | – | データの規模に影響を受けやすい | – |
計算方法

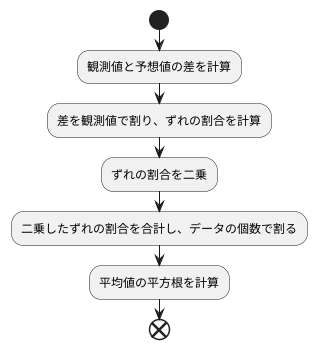
計算方法は、名前が示す通り、いくつかの段階を踏みます。まず、観測された数値と予想された数値の差を計算します。これは、観測値を基準として、予想がどれほどずれているかを示すものです。このずれを、観測された数値で割ることで、ずれの割合を求めます。この割合は、観測値に対するずれの大きさを相対的に示すもので、百分率で表されます。
次に、それぞれのデータ点について計算したずれの割合を二乗します。二乗することにより、ずれの大きさが強調され、大きなずれを持つデータ点が計算結果に与える影響が大きくなります。また、正負の符号が打ち消し合うのを防ぐ効果もあります。そして、二乗したずれの割合をすべて合計し、データの個数で割ります。これで、二乗したずれの割合の平均値が求まります。
最後に、求めた平均値の平方根を計算します。平方根を計算することで、二乗によって強調されたずれの大きさを元のスケールに戻し、ずれの割合の平均的な大きさを示す値が得られます。これが、計算方法の最終的な結果であり、二乗平均平方根誤差と呼ばれます。
数式で表すと、予想値をyᵢ、観測値をŷᵢ、データの個数をnとした場合、二乗平均平方根誤差 = √(1/n * Σᵢ((yᵢ – ŷᵢ)/ŷᵢ)² )となります。この式からもわかるように、二乗平均平方根誤差は、観測値に対するずれの割合を評価しているため、観測値がゼロに近い場合には、計算結果が不安定になることがあります。このような場合には、分母に小さな定数を加えるなどの工夫が必要です。一方で、二乗平均平方根誤差は百分率で表されるため、計算結果の意味を理解しやすいという利点があります。たとえば、二乗平均平方根誤差が10%であれば、予想値は平均的に観測値から10%ずれていると解釈できます。
他の指標との比較

様々な計算方法で誤差を評価する指標が存在します。それぞれの指標には異なる特性があり、状況に応じて適切な指標を選ぶ必要があります。代表的な指標である平均二乗誤差の平方根、平均絶対誤差、そして平均二乗パーセント誤差を比較してみましょう。
平均二乗誤差の平方根は、誤差を二乗してから平均をとり、最後に平方根を計算します。このため、大きな誤差はより大きな値となり、結果に大きく影響します。例えば、ある商品の売上げ数を予測する際に、大きく外れた予測は、在庫管理などに大きな影響を与えるため、この指標を用いることで、大きな誤差を避けるようにモデルを調整できます。
一方、平均絶対誤差は、誤差の絶対値を平均するだけのシンプルな計算方法です。そのため、平均二乗誤差の平方根と比べると、大きな誤差の影響は少なくなります。多少の誤差は許容できるが、全体的な予測の正確さを重視したい場合に適しています。
平均二乗パーセント誤差は、誤差を実際の値で割るという点で、前述の二つの指標とは大きく異なります。これは、相対的な誤差を評価することを意味します。例えば、高額な商品の売上げ予測と、安価な商品の売上げ予測を比較する場合、単純な誤差の大きさだけでは比較できません。高額な商品は、少数の誤差でも金額が大きくなりやすいからです。平均二乗パーセント誤差を用いることで、それぞれの商品の予測精度を相対的に比較することができます。
このように、どの指標を用いるかは、データの性質や分析の目的に大きく依存します。それぞれの指標の特徴を理解し、適切な指標を選択することで、より正確で意味のある分析を行うことができます。
| 指標 | 計算方法 | 特徴 | 適用例 |
|---|---|---|---|
| 平均二乗誤差の平方根 (RMSE) | 誤差を二乗し平均、平方根 | 大きな誤差の影響大 | 大きな誤差を避けたい場合 (在庫管理など) |
| 平均絶対誤差 (MAE) | 誤差の絶対値の平均 | 大きな誤差の影響小、全体的な正確さ重視 | 多少の誤差は許容できる場合 |
| 平均二乗パーセント誤差 (RMSPE) | 誤差を実際の値で割る、相対的な誤差 | 金額が異なる商品の比較 | 高額商品と安価商品の予測比較など |
適用事例

需要予測や売上予測といった、将来の値を推測する場面で、予測の確からしさを測ることはとても大切です。予測の良し悪しを測る尺度の一つとして、平均平方二乗誤差率(RMSPE)という方法があります。これは、実際の値と予測値のずれを、実際の値の大きさで割ることで、ずれの割合を計算し、その平均を見ることで、予測の精度を評価するものです。
例えば、小売店で、ある商品の売れ行きを予測することを考えてみましょう。RMSPEを使うことで、過去の売れ行きデータと予測値を比較し、予測の精度を調べることができます。もしRMSPEの値が小さければ、予測が実際の売れ行きに近いと言えるでしょう。逆に値が大きければ、予測が外れている可能性が高く、予測モデルの見直しが必要となります。
製造業でもRMSPEは役立ちます。工場で作られる製品の数を予測する場合、RMSPEを使って予測の正確さを評価することができます。製品の数が多ければ、予測の誤差も大きくなる可能性がありますが、RMSPEは割合で考えるため、製品数の大小に関わらず、予測の精度を一貫して評価することができます。
金融の世界でもRMSPEは使われています。株の値段や為替のレートは、日々大きく変動します。これらの変動を予測するモデルを作る際、RMSPEを使ってモデルの精度を測ることができます。変動の幅が大きい場合でも、RMSPEは相対的な誤差を見るため、安定した評価を行うことができます。
季節によって売上が大きく変わる商品を扱う場合、通常の誤差計算では、売上の多い時期の誤差が全体の評価に大きく影響してしまう可能性があります。しかし、RMSPEを使うことで、それぞれの時期の売上に対する相対的な誤差を評価できるため、より正確な予測モデルの評価が可能となります。このように、RMSPEは様々な分野で予測モデルの評価に役立っています。
| 分野 | RMSPEの活用例 | メリット |
|---|---|---|
| 小売 | 商品の売れ行き予測 | 過去の売れ行きデータと予測値を比較し、予測精度を評価 |
| 製造業 | 製品数の予測 | 製品数の大小に関わらず、予測精度を一貫して評価 |
| 金融 | 株価や為替レートの予測 | 変動の幅が大きい場合でも、安定した評価が可能 |
| 季節性のある商品 | 季節変動のある商品の売上予測 | 売上の多い時期の誤差が全体の評価に大きく影響するのを防ぎ、より正確な評価が可能 |
注意点

予測の正確さを測る指標の一つである平方平均二乗誤差率(RMSPE)を使う際には、いくつか気を付けなければならない点があります。まず、実際の値がゼロに近い場合、計算結果が大きく変動してしまうことがあります。これは、RMSPEの計算式で、実際の値を分母に使っているためです。ゼロに近い値で割ると、結果が非常に大きくなってしまい、正確な評価ができなくなります。このような問題を防ぐためには、分母に小さな値を足すなどの工夫が必要です。
次に、RMSPEは大きく外れた値の影響を受けやすいという点にも注意が必要です。もし、データの中に極端に大きい値や小さい値が含まれていると、RMSPEの値がそれらの値に引っ張られてしまい、全体的な傾向を正しく反映しない可能性があります。ですから、データに外れた値が含まれている場合は、あらかじめそれらの値を取り除くか、他の指標も一緒に使って評価することが大切です。
さらに、RMSPEは相対的な誤差を評価する指標であるため、予測値の大きさそのものについては何も教えてくれません。例えば、RMSPEの値が小さくても、予測値が常に実際の値よりも小さくなっている場合、業務上の判断に悪い影響を与える可能性があります。RMSPEが小さいということは、実際の値に対する誤差の割合が小さいということを意味するだけで、予測値そのものの正確さを示すものではありません。
そのため、より正確な評価を行うためには、RMSPEだけでなく、平均絶対誤差(MAE)や平均二乗誤差(RMSE)といった他の指標も合わせて使うことが重要です。MAEは予測値と実際の値の差の絶対値の平均を、RMSEは予測値と実際の値の差の二乗の平均の平方根を表します。これらの指標も併用することで、予測モデルの性能を様々な角度から見て、より深く理解することができます。
| 注意点 | 説明 | 対策 |
|---|---|---|
| ゼロに近い値での不安定性 | 実際の値がゼロに近い場合、RMSPEの計算結果が大きく変動する。これは、RMSPEの計算式で、実際の値を分母に使っているため。 | 分母に小さな値を足す。 |
| 外れ値の影響を受けやすい | データの中に極端に大きい値や小さい値が含まれていると、RMSPEの値がそれらの値に引っ張られてしまい、全体的な傾向を正しく反映しない。 | 外れ値を取り除くか、他の指標も一緒に使う。 |
| 予測値の大きさの情報がない | RMSPEは相対的な誤差を評価する指標であるため、予測値の大きさそのものについては何も教えてくれない。RMSPEが小さくても、予測値が常に実際の値よりも小さくなっている場合、業務上の判断に悪い影響を与える可能性がある。 | MAE、RMSEなどの他の指標も合わせて使う。 |
まとめ

あらゆる分野で、機械学習の活用が進んでいます。そして、作成した学習器の良し悪しを測る評価指標は、学習器の改良や選定に欠かせません。数ある指標の中でも、平均二乗平方根誤差(RMSPE)は、相対的な誤差を評価できるという点で、大変有用です。
RMSPEは、実測値と予測値の差を二乗し、それを実測値で割った値の平均の平方根です。そのため、異なる規模のデータ群を比較する際に、その真価を発揮します。例えば、売上高のように、企業によって規模が大きく異なるデータを扱う場合、絶対的な誤差ではなく、相対的な誤差で評価することが大切です。RMSPEであれば、規模の差に左右されずに、予測の正確さを評価できます。また、実測値のばらつきが大きいデータ群を扱う場合にも、RMSPEは有効です。実測値が大きいほど、予測値との差も大きくなる傾向がありますが、RMSPEは実測値で割ることで、この影響を緩和し、より安定した評価を可能にします。
しかし、RMSPEを用いる際には、いくつか注意すべき点があります。実測値がゼロに近い場合、RMSPEの計算は不安定になる可能性があります。これは、ゼロで割ることになってしまうためです。このような場合は、RMSPE以外の指標を検討するか、データの前処理を行う必要があります。また、RMSPEは外れ値の影響を受けやすいという欠点もあります。極端に大きな、あるいは小さな実測値が存在する場合、RMSPEの値が大きく歪められる可能性があります。そのため、外れ値の処理も重要です。
RMSPEは万能ではありませんが、他の指標と併用することで、より的確なモデル評価を行うことができます。例えば、平均絶対誤差(MAE)や決定係数などと合わせて用いることで、モデルの特性を多角的に捉えることができます。目的に合った指標を選び、その特性を理解した上で活用することで、より精度の高い学習器の構築に繋がるでしょう。RMSPEは、今後も機械学習の発展に大きく貢献していくことが期待されます。
| 指標名 | 説明 | 利点 | 欠点 | 使用上の注意 |
|---|---|---|---|---|
| RMSPE (平均二乗平方根誤差) | 実測値と予測値の差を二乗し、それを実測値で割った値の平均の平方根 | ・相対的な誤差を評価できる ・異なる規模のデータ群を比較できる ・実測値のばらつきが大きいデータ群を扱う場合にも有効 |
・実測値がゼロに近い場合、計算が不安定になる ・外れ値の影響を受けやすい |
・実測値がゼロに近い場合は、他の指標を検討するか、データの前処理を行う ・外れ値の処理を行う ・他の指標(MAE、決定係数など)と併用する |
