次元の呪いとは?高次元データの課題と解決策

AIを知りたい
「次元の呪い」って、データの組み合わせが増えすぎるのが原因で起こるんですよね?でも、ビッグデータって、たくさんのデータがあるほど良いんじゃないんですか?

AIエンジニア
良い質問だね。確かにデータは多い方が良いんだけど、データの種類が増えすぎると、その分だけ組み合わせが爆発的に増えてしまうんだ。例えば、10種類のデータそれぞれに10個の値があるとすると、全部で100億通りの組み合わせになる。種類が増えれば増えるほど、組み合わせはもっとすごい勢いで増えていくんだよ。

AIを知りたい
なるほど。じゃあ、たくさんの種類のデータがあると、コンピュータの計算が追いつかなくなるってことですか?

AIエンジニア
その通り!計算に時間がかかりすぎるだけでなく、データの組み合わせが多すぎて、AIがうまく学習できないこともあるんだ。だから、「次元の呪い」を避けるには、本当に必要なデータだけを選ぶ必要があるんだよ。
次元の呪いとは。
人工知能に関わる言葉で「次元の呪い」というものがあります。これは、機械学習の方法を使う際に、うまく力を発揮できず、初めて見るデータに対してきちんと予測することが難しくなる状態のことです。なぜこうなるかというと、データの種類が多くなりすぎ、データの組み合わせが膨大になりすぎるためです。大量のデータを処理できる計算機を用意していても、「次元の呪い」に気をつけないと、計算に莫大な費用がかかるだけでなく、十分な学習結果が得られず、新しいデータにうまく対応できないといった問題が起こってしまいます。この「次元の呪い」を解決するには、データの特徴を作り出したり、必要な特徴を選び出す作業が必要になります。
次元の呪いとは

「次元の呪い」とは、機械学習の分野でよく耳にする言葉です。これは、扱うデータの次元数、つまり特徴量の数が多くなるにつれて、機械学習モデルの性能が思わぬ方向に悪くなっていく現象を指します。
一見すると、たくさんの情報を含む高次元データは、より的確な予測を導き出すための鍵のように思えます。データが多ければ多いほど、より現実に近い予測ができるはずだと考えるのは自然なことです。しかし、次元が増えるということは、データが存在する空間が想像を絶する速さで広がることを意味します。例えるなら、二次元の世界が平面だとすれば、三次元の世界は立体になり、さらに次元が増えると、私たちが認識できる空間の形を超えてしまいます。
このように広大なデータ空間では、たとえデータの量が多くても、それぞれのデータ点はまばらに散らばり、まるで宇宙の星のように希薄な存在になってしまいます。結果として、機械学習モデルはデータ全体の傾向を掴むのが難しくなり、全体像を見失ってしまいます。
この状態は、まるで広大な砂漠で小さな宝石を探すようなものです。いくら砂漠全体に宝石が散らばっていても、砂漠の広大さに阻まれて、なかなか宝石を見つけ出すことはできません。同様に、高次元データでは、データの量が豊富に見えても、実際にはデータ同士の関連性を見つけるのが難しく、有効な情報を取り出すのが困難になります。
さらに、データがまばらになると、わずかなノイズ(余計な情報)の影響を受けやすくなります。まるで静かな湖面に小石を投げ込んだ時に、波紋が広がるように、高次元データではノイズが予測結果を大きく歪めてしまう可能性があります。このため、せっかく大量のデータを集めても、かえって予測の正確さが失われてしまうという皮肉な結果につながるのです。つまり、「次元の呪い」とは、データ量の増加が必ずしも良い結果をもたらすとは限らないという、機械学習における重要な課題なのです。
| 項目 | 説明 |
|---|---|
| 次元の呪い | 機械学習において、データの次元数(特徴量の数)が増えることで、モデルの性能が劣化してしまう現象。 |
| 高次元データの問題点 | データ空間が膨大になり、データがまばらに分布するため、モデルが全体像を把握しにくくなる。 |
| 高次元データの例え | 広大な砂漠で宝石を探すようなもの。データは豊富だが、関連性を見つけるのが困難。 |
| ノイズの影響 | データがまばらなため、ノイズの影響を受けやすく、予測結果が歪みやすい。 |
| 結論 | データ量の増加は必ずしも良い結果につながらない。 |
次元の呪いがもたらす問題点

高次元データを取り扱う際に現れる「次元の呪い」は、機械学習の様々な場面で問題を引き起こします。この現象は、データの次元数が大きくなるにつれて、データ空間が加速度的に広がってしまうことに起因します。この空間の広がりは、一見問題ないように思えるかもしれませんが、実際には様々な困難をもたらします。
まず、計算量の増大という深刻な問題があります。次元が増えるごとに、モデルの学習や予測に必要な計算量は指数関数的に増加します。例えば、ある計算が2次元データで1分かかるとすると、同じ計算を3次元データで行うと、場合によっては数倍の時間がかかります。さらに次元が増えると、計算時間はあっという間に膨れ上がり、現実的な時間内で計算を終えることが不可能になる場合もあります。
次に、過学習のリスクが高まります。高次元空間では、データはまばらに分布する傾向があります。限られた量のデータで複雑なモデルを学習しようとすると、モデルはデータの背後にある真の関係性を捉えることができず、ノイズや偶然のばらつきまで学習してしまいます。これは、訓練データにはよく適合するものの、未知のデータに対しては全く役に立たないモデルを生み出すことになります。
さらに、データの可視化も困難になります。私たちは、2次元や3次元のデータであれば、散布図やグラフを用いて容易に可視化し、データの傾向や特徴を把握することができます。しかし、4次元以上のデータになると、人間の認知能力の限界から、可視化は極めて難しくなります。そのため、データの理解や分析が妨げられ、適切なモデルの選択や評価が難しくなります。
このように、次元の呪いは、計算時間、モデルの精度、データ解析の容易さなど、機械学習の様々な側面に悪影響を及ぼします。高次元データを扱う際には、この問題を意識し、次元削減などの対策を講じる必要があります。
| 問題点 | 詳細 |
|---|---|
| 計算量の増大 | 次元数の増加に伴い、計算量が指数関数的に増加し、現実的な時間内で計算が完了しない可能性がある。 |
| 過学習のリスク増加 | 高次元空間ではデータがまばらになり、モデルがノイズを学習し、未知データに役に立たないモデルとなる。 |
| データ可視化の困難さ | 4次元以上のデータは人間の認知能力を超え、可視化が困難になり、データの理解や分析が妨げられる。 |
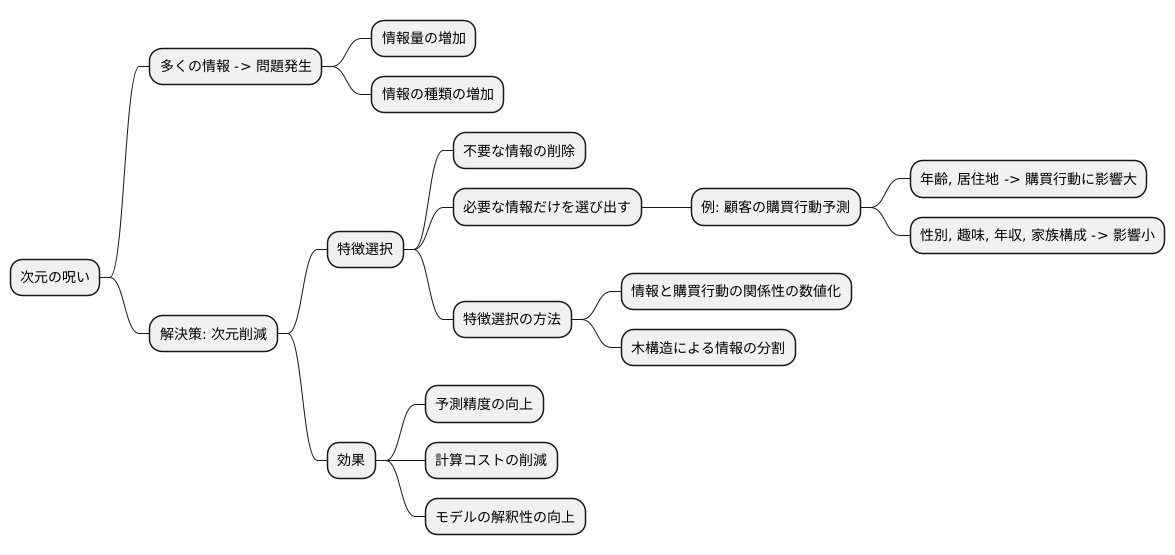
高次元データへの対処法:特徴選択

多くの情報を取り扱う時代になり、集まる情報の量も種類も増えてきました。こうしたたくさんの情報を分析する際に、情報の次元数が多すぎることで問題が生じることがあります。これを次元の呪いと呼びます。例えば、顧客の購買行動を予測する場合、年齢や性別、居住地だけでなく、趣味や年収、家族構成など、様々な情報を集めることができます。しかし、これらの情報全てを使うと、予測モデルを作るのが難しくなり、正確な予測ができなくなることがあります。
この問題に対処するためには、情報の次元数を減らす必要があります。そのための方法の一つとして、特徴選択というものがあります。特徴選択とは、たくさんの情報の中から、本当に必要な情報だけを選び出すことです。顧客の購買行動の例で言えば、年齢、性別、居住地、趣味、年収、家族構成など、たくさんの情報の中から、本当に購買行動に影響を与える重要な情報だけを選び出す作業です。例えば、過去の購買データから、年齢と居住地が購買行動に大きく影響していることが分かれば、それ以外の情報、つまり性別、趣味、年収、家族構成などは使わないという選択ができます。
特徴選択には様々な方法があります。それぞれの情報と購買行動との関係の強さを数値で表し、関係の強い情報だけを選ぶ方法や、木の枝のように情報を分けていくことで重要な情報を見つけ出す方法などがあります。どの方法を使うかは、扱う情報の種類や目的によって異なります。
適切な特徴選択を行うことで、次元の呪いを避け、より正確な予測モデルを作ることができます。不要な情報を削除することで、モデルを作る計算の手間も減り、結果が出るまでの時間も短縮できます。また、モデルが単純になることで、なぜその予測結果になったのかを説明しやすくなるという利点もあります。
高次元データへの対処法:特徴作成

多くの情報を取り扱う場合、データの次元数が非常に大きくなることがあります。このような高次元データは、計算に時間がかかったり、モデルの精度が低下したりするなどの問題を引き起こす可能性があります。そこで、高次元データに対処するための有効な手段として、特徴作成という方法があります。
特徴作成とは、元からあるデータの特徴を組み合わせて、あるいは変換して、新たな特徴を作り出す手法です。例として、顧客の年齢と性別の情報があるとします。これらの情報を別々に扱うのではなく、「20歳代の男性」「30歳代の女性」といった具合に組み合わせることで、新たな特徴を作り出すことができます。このように、複数の特徴を組み合わせることで、より具体的な情報を表現する特徴を作成することが可能になります。
また、データの変換も有効な手段です。例えば、数値データに対しては、対数変換や平方根変換といった数学的な処理を施すことで、データの分布形状を変えることができます。元のデータが偏っている場合でも、変換によってデータの分布を滑らかにし、モデルの精度向上に繋がることがあります。カテゴリデータの場合、例えば色を表現する「赤」「青」「緑」のようなデータは、そのままでは計算に用いることができません。このようなデータに対しては、それぞれのカテゴリに該当するかどうかを0か1で表すone-hotエンコーディングと呼ばれる手法を用いて数値データに変換することで、モデルで利用できるようになります。
このように、特徴作成は、既存の特徴を組み合わせたり変換したりすることで、より予測に役立つ新たな特徴を生み出すことができます。結果として、モデルの精度向上や計算時間の短縮といった効果が期待できます。高次元データに直面した際には、特徴作成を検討することで、より効果的なデータ活用が可能になります。
| 手法 | 説明 | 例 | 効果 |
|---|---|---|---|
| 特徴の組み合わせ | 元からあるデータの特徴を組み合わせて、新たな特徴を作り出す。 | 年齢と性別を組み合わせて「20歳代の男性」「30歳代の女性」といった特徴を作成 | より具体的な情報を表現する特徴を作成可能 |
| データの変換(数値データ) | 対数変換や平方根変換といった数学的処理を施すことで、データの分布形状を変える。 | 偏った数値データを滑らかにする | モデルの精度向上 |
| データの変換(カテゴリデータ) | One-hotエンコーディングを用いて数値データに変換する。 | 色を表現する「赤」「青」「緑」を0または1の数値データに変換 | モデルで利用可能になる |
次元削減:多様体学習

高次元データは、扱うのが大変な場合があります。多くの変数を持つため、計算量が膨大になったり、データの可視化が困難になったりします。そこで、データの本質的な構造を保ちつつ、次元数を減らす手法が求められます。このような手法の一つが多様体学習です。
多様体学習は、高次元データは実際にはもっと低次元の構造(多様体)に沿って分布しているという考えに基づいています。例えば、くるくると丸まった紙を想像してみてください。紙自体は二次元の平面ですが、丸まった状態では三次元空間に存在しています。同様に、高次元データも、実際にはもっと低次元の多様体に埋め込まれている可能性があります。
この多様体の形を見つけることで、データの主要な特徴を捉えつつ次元数を削減できます。次元削減により、データの可視化が容易になるだけでなく、機械学習モデルの学習効率向上や過学習の抑制といった効果も期待できます。
多様体学習には様々な手法がありますが、代表的なものとして主成分分析(PCA)とt-SNEが挙げられます。PCAは、データの分散が最大になる方向を見つけ出し、その方向にデータを射影することで次元を削減します。一方、t-SNEは、高次元空間でのデータ点間の距離関係を低次元空間でもなるべく保つようにデータを配置することで次元削減を行います。PCAは線形的な次元削減手法であるのに対し、t-SNEは非線形的な次元削減手法であり、複雑な形状の多様体にも対応できます。
このように、多様体学習による次元削減は、高次元データを扱う上で強力な道具となります。目的に合わせて適切な手法を選択することで、データ分析や機械学習の様々な場面で役立てることができます。
| 項目 | 説明 |
|---|---|
| 高次元データの問題点 | 計算量の増大、データ可視化の困難 |
| 多様体学習 | 高次元データは低次元の多様体に沿って分布しているという考えに基づき、次元数を削減する手法 |
| 多様体学習のメリット | データの可視化、機械学習モデルの学習効率向上、過学習の抑制 |
| 主成分分析 (PCA) | データの分散が最大になる方向への射影による線形的な次元削減手法 |
| t-SNE | 高次元空間でのデータ点間の距離関係を低次元空間でも保つ非線形的な次元削減手法 |
適切な手法の選択

高次元データの解析は「次元の呪い」という問題を引き起こし、データの希薄化や計算コストの増大につながることがあります。この問題に対処するためには、データの特性や分析の目的に最適な手法を選択する必要があります。代表的な手法として、特徴選択、特徴作成、多様体学習が挙げられます。
特徴選択は、既存の特徴量の中から、分析に関連性の高い特徴量を選び出す手法です。この手法の利点は、解釈性が高いことです。つまり、どの特徴量が重要なのかを分かりやすく示すことができます。そのため、データの背後にあるメカニズムの理解に役立ちます。例えば、顧客の購買行動を分析する場合、年齢や収入といった特徴量が購買に大きく影響していることが分かれば、効果的な販売戦略を立てることができます。ただし、既に存在する特徴量から選ぶため、最適な特徴量が存在しない場合もあります。
一方、特徴作成は、既存の特徴量を組み合わせて、新たな特徴量を作り出す手法です。例えば、身長と体重から肥満度指数(BMI)を計算するなどが挙げられます。この手法は、より強力な予測能力を持つ特徴量を生み出す可能性を秘めています。しかし、専門的な知識や多くの試行錯誤が必要となる場合もあります。最適な組み合わせを見つけるためには、試行錯誤を繰り返す必要があるからです。
多様体学習は、高次元データが低次元の多様体上に分布していると仮定し、その多様体の構造を学習する手法です。これは、データの背後にある本質的な構造を捉えるのに役立ちます。高次元空間で複雑に絡み合ったデータも、多様体学習を用いることで、より単純な構造として捉えることができる可能性があります。しかし、多様体学習は複雑な計算を伴うことが多く、計算コストが高い場合があります。
このように、それぞれの手法には長所と短所があります。どの手法が最適かは、データの性質や分析の目的によって異なります。適切な手法を選択することで、次元の呪いを効果的に克服し、高次元データから有益な知見を抽出することができます。
| 手法 | 説明 | 長所 | 短所 | 例 |
|---|---|---|---|---|
| 特徴選択 | 既存の特徴量から分析に関連性の高い特徴量を選び出す。 | 解釈性が高い | 最適な特徴量が存在しない場合もある | 顧客の購買行動分析における年齢や収入 |
| 特徴作成 | 既存の特徴量を組み合わせて、新たな特徴量を作り出す。 | より強力な予測能力を持つ特徴量を生み出す可能性 | 専門的な知識や多くの試行錯誤が必要となる場合もある | 身長と体重から肥満度指数(BMI)を計算 |
| 多様体学習 | 高次元データが低次元の多様体上に分布していると仮定し、その多様体の構造を学習する。 | データの背後にある本質的な構造を捉えるのに役立つ | 計算コストが高い場合がある | – |
