次元の呪い:高次元データの罠

AIを知りたい
先生、「次元の呪い」ってどういう意味ですか?難しそうでよくわからないです。

AIエンジニア
そうだね、少し難しい概念だね。「次元の呪い」とは、予測モデルを作る際に、入力データの特徴量が増えれば増えるほど、正確な予測をするために必要なデータ量が爆発的に増えてしまう現象のことだよ。例えば、人の顔を認識するAIを作るとしよう。目の大きさ、鼻の高さ、口の幅など、特徴量を増やすほど、より正確に顔を認識できるようになるよね。

AIを知りたい
なるほど。特徴量を増やすと正確さが増すのはわかるのですが、なぜデータ量が爆発的に増えてしまうのですか?

AIエンジニア
いい質問だね。簡単に言うと、特徴量が増えるごとに、データが存在する空間が広くなってしまうんだ。想像してみて。1つの特徴量なら直線、2つなら平面、3つなら立体空間…と、特徴量が増えるごとに空間の広がり方も大きくなるよね?その広大な空間を埋め尽くすだけのデータが必要になるから、データ量が爆発的に増えてしまうんだよ。これが「次元の呪い」だ。
次元の呪いとは。
人工知能の分野でよく使われる「次元の呪い」という言葉について説明します。これは、機械学習モデルに入力するデータの特徴が増えるほど、良い精度を出すために必要なデータ量が爆発的に増えてしまう現象のことです。たとえば、顔認識をするとき、目の大きさや鼻の形など、顔の特徴をたくさんデータとして与えると、一見すると精度の高い認識ができそうですが、実際には、その分だけ大量のデータが必要になってしまい、学習が難しくなります。この現象を「次元の呪い」と呼んでいます。
次元の呪いとは

機械学習では、様々な情報をもとに予測を行います。この情報一つ一つを次元と呼びます。例えば、家の値段を予測する際には、部屋の広さや築年数といった情報が次元となります。これらの次元が多いほど、一見、より正確な予測ができそうに思えます。しかし、実際にはそう単純ではありません。次元が増えるほど、予測に必要な情報量も爆発的に増えてしまうのです。これが次元の呪いと呼ばれる現象です。
例えて言うなら、一枚の地図上に点を打つことを考えてみましょう。もし地図が一枚だけであれば、点を密集させて配置することができます。しかし、地図が何枚も重なった立体的な空間になると、同じ数の点を配置しても、点と点の間隔は広がってしまいます。次元が増えるということは、この地図の枚数が増えることと同じです。次元が増えるにつれて、データが存在する空間は広がり、データ同士の距離が離れてまばらになるのです。
まばらになったデータから正確な予測をするためには、より多くのデータが必要です。少ないデータでは、データ間の関係性を正確に捉えることができず、予測の精度が低下してしまいます。まるで、広い砂漠で、数少ない砂の粒から砂漠全体の形を推測しようとするようなものです。
この次元の呪いを避けるためには、次元削減という手法を用います。これは、重要な情報だけを残して次元の数を減らす技術です。例えば、家の値段を予測する際に、家の色よりも部屋の広さのほうが重要だと判断した場合、色の情報を削除することで次元を減らすことができます。このように、本当に必要な情報を見極めて次元を減らすことで、次元の呪いを克服し、より正確な予測モデルを作ることができるのです。
高次元空間の特殊な性質

私たちが普段生活している空間は、縦・横・高さの三つの尺度で捉えることができます。これは三次元空間と呼ばれています。しかし、扱うデータによっては、もっと多くの尺度、つまり次元が必要になることがあります。例えば、ある製品の評価を考える際に、価格、性能、デザイン、耐久性など、様々な要素を考慮する必要があるでしょう。これらの要素一つ一つが次元となります。このように多くの尺度を必要とする空間を高次元空間と呼びます。
高次元空間には、私たちの直感に反する不思議な性質があります。低次元、例えば二次元や三次元では、データは空間内に比較的均等に分布しています。しかし、次元が増えるにつれて、データ間の距離に変化が生じます。データ同士の距離は広がり、ほとんどのデータが空間の端、つまり境界付近に集まるようになるのです。ちょうど風船の表面に点が散らばっている様子を想像してみてください。風船の表面積が大きくなるほど、点はまばらになり、互いの距離は遠くなります。高次元空間もこれと同じように、次元が増えるほどデータがまばらになり、空間の大部分が空っぽになってしまいます。これを「次元の呪い」と呼びます。
次元の呪いは、機械学習において大きな問題を引き起こします。限られた量のデータで高次元空間全体を網羅することは不可能です。まるで広大な砂漠で数粒の砂を探すようなものです。データがまばらなため、学習に使えるデータが不足し、学習モデルは限られたデータの特徴に過剰に適応してしまいます。これは、学習データに対する精度は高いものの、未知のデータに対する予測能力は低いという、過剰適合と呼ばれる状態を引き起こします。結果として、モデルは現実世界の問題に対してうまく機能しなくなってしまいます。そのため、高次元データを扱う際には、次元削減などの適切な対処法が必要不可欠となります。
次元の呪いの影響

多くの情報を取り扱う機械学習において「次元の呪い」は、モデルの性能を大きく左右する深刻な問題です。この問題は、扱う情報の次元、つまり特徴量の数が多くなるほど顕著に現れます。
次元の呪いの最初の影響は、必要な学習データ量の爆発的な増加です。次元が増えるごとに、データを十分に網羅するために必要なデータ量は、まるで雪だるま式に膨れ上がります。二次元であれば平面を覆うデータ量で済みますが、三次元になると空間全体を満たす必要があり、さらに高次元になることを想像してみてください。現実世界の限られた時間や費用では、必要なデータを集めることは到底不可能となります。
さらに、高次元空間ではデータがまばらに分布する傾向があります。これは、同じデータ量でも、次元が増えるほどデータ間の距離が遠くなり、空間の大部分が空っぽになってしまうからです。このデータのまばらさは、モデルの学習に悪影響を及ぼします。まるで霧の中に迷い込んだように、モデルはデータの全体像を捉えられず、わずかなノイズに過剰に反応してしまうのです。結果として、学習データには高い精度を示すにも関わらず、新しい未知のデータに対しては予測精度が低い、いわゆる過学習の状態に陥ってしまいます。
これは、モデルが学習データの表面的な特徴にのみ囚われ、データに潜む本質的な関係性を理解できていないことを意味します。まるで暗闇の中で、壁や床の触感だけで部屋の形を推測しようとするようなものです。限られた情報から全体像を把握することは非常に困難であり、真の姿を捉えることはできません。次元の呪いは、このような困難さを機械学習モデルにもたらし、高精度な予測を阻む大きな壁となっているのです。
| 問題点 | 説明 | 結果 |
|---|---|---|
| 学習データ量の爆発的増加 | 次元が増えるごとに、データを十分に網羅するために必要なデータ量は急激に増加する。 | 現実的な時間と費用で必要なデータ収集が不可能になる。 |
| データのまばらな分布 | 高次元空間では、データ間の距離が遠くなり、空間の大部分が空っぽになる。 | モデルがデータの全体像を捉えられず、ノイズに過剰反応し、過学習を引き起こす。未知のデータへの予測精度が低下する。 |
次元の呪いへの対策

多くの情報を持つデータは、一見有益に見える一方で、落とし穴も潜んでいます。情報量の多さは、データの次元、つまり特徴量の多さに繋がります。特徴量が増えることで、データの空間はより広く、そしてまばらになります。これを次元が高い状態、高次元空間と呼びます。高次元空間では、データ同士がまばらに存在することになり、一見豊富に見えるデータも実はスカスカな状態になってしまいます。この現象は次元の呪いと呼ばれ、機械学習モデルの性能低下を引き起こす原因となります。
この次元の呪いに対処する有効な手段の一つとして、次元削減があります。次元削減とは、文字通りデータの次元数を減らすことです。重要な情報を保ちつつ、不要な特徴量を削ぎ落とすことで、データ空間を縮小し、次元の呪いを回避します。よく使われる手法の一つに、主成分分析があります。これは、データのばらつきが最も大きい方向を見つけ出し、その方向にデータを射影することで次元を減らす方法です。他にも、線形判別分析という手法も存在します。これは、異なる種類のデータをよりよく分離するように次元を削減する手法で、分類問題に有効です。これらの手法を用いることで、データのまばらさを解消し、少ないデータ量でもモデルを効率的に学習させることが可能になります。
もう一つの有効な対策として、正則化という手法があります。複雑なモデルは、学習データに過剰に適応し、未知のデータに対する予測性能が低下する、いわゆる過学習を起こしやすくなります。正則化は、モデルの複雑さを抑えることで、この過学習を防ぎます。代表的な方法として、L1正則化とL2正則化があります。これらの手法は、モデルのパラメータに制約を加えることで、高次元空間でのノイズの影響を軽減し、モデルを安定させます。L1正則化は、不要な特徴量に対応するパラメータをゼロに近づける性質があり、特徴量の選択にも役立ちます。L2正則化は、全てのパラメータを小さくすることで、モデルの複雑さを抑制します。状況に応じて適切な正則化手法を選ぶことで、モデルの性能向上に繋がります。
| 問題点 | 手法 | 説明 | 種類/詳細 |
|---|---|---|---|
| 次元の呪い | 次元削減 | 重要な情報を保ちつつ、不要な特徴量を削ぎ落とすことで、データ空間を縮小し、次元の呪いを回避 | 主成分分析: データのばらつきが最も大きい方向を見つけ出し、その方向にデータを射影することで次元を減らす |
| 線形判別分析: 異なる種類のデータをよりよく分離するように次元を削減、分類問題に有効 | |||
| 正則化 | モデルの複雑さを抑えることで、過学習を防ぐ | L1正則化: 不要な特徴量に対応するパラメータをゼロに近づける、特徴量の選択にも役立つ L2正則化: 全てのパラメータを小さくすることで、モデルの複雑さを抑制 |
特徴量選択の重要性

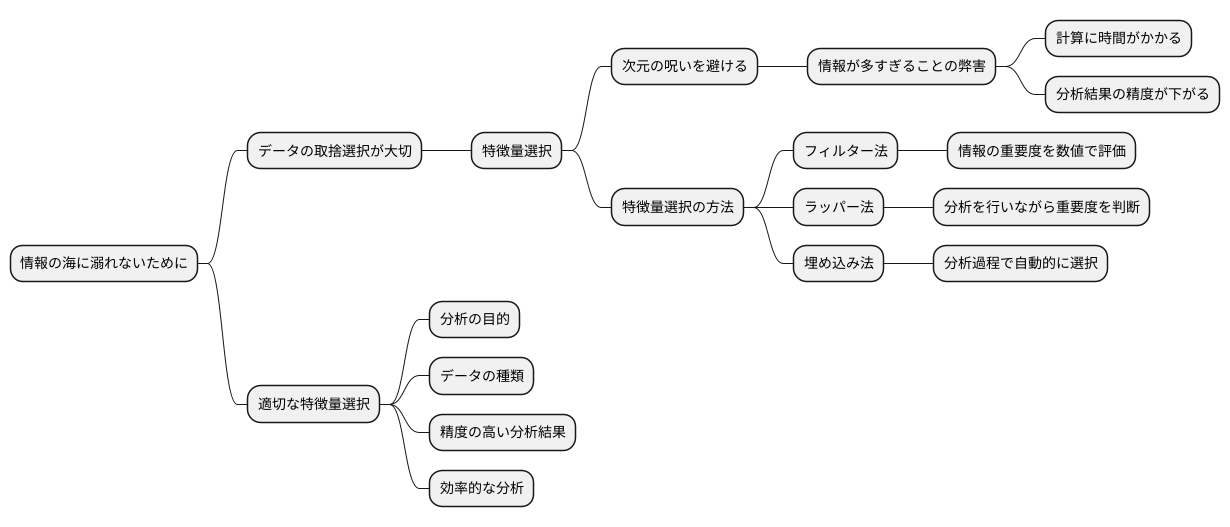
情報の海に溺れないために、データの取捨選択が大切です。これを特徴量選択といいます。データ分析をする際、たくさんの情報があると、一見良さそうに思えます。しかし、情報が多すぎると、逆に分析が難しくなることがあります。これを次元の呪いと呼びます。次元の呪いにかかると、計算に時間がかかったり、分析結果の精度が下がったりするなどの問題が発生します。
特徴量選択は、この次元の呪いを避けるための重要な方法です。たくさんの情報の中から、本当に必要な情報だけを選び出すことで、分析をスムーズに進めることができます。不要な情報は取り除き、必要な情報だけを残すことで、次元の呪いの影響を減らすことができるのです。
特徴量選択には、色々な方法があります。大きく分けて、フィルター法、ラッパー法、埋め込み法の三種類があります。フィルター法は、それぞれの情報がどれだけ大切かを数値で評価し、その数値に基づいて情報をふるいにかける方法です。例えば、ある情報と分析結果との関係性が強ければ、その情報は重要と判断します。ラッパー法は、実際に分析を行いながら、どの情報が重要かを判断する方法です。色々な情報の組み合わせで分析を行い、最も良い結果が得られる組み合わせを選びます。埋め込み法は、分析の過程で自動的に重要な情報を選び出す方法です。
どの方法を使うかは、分析の目的やデータの種類によって異なります。例えば、分析結果の正確さを重視する場合と、計算にかかる時間を短縮したい場合では、選ぶべき方法が変わってきます。また、データの種類によっても、適切な方法は異なります。それぞれの方法の特徴を理解し、状況に応じて適切な方法を選ぶことが大切です。適切な特徴量選択を行うことで、精度の高い分析結果を効率的に得ることができます。
データの理解と準備

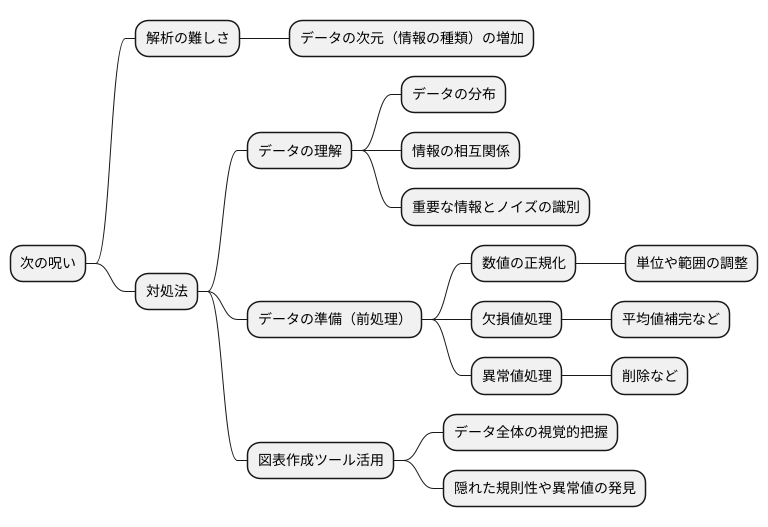
多くの情報を持つデータは、一見すると有益な情報を持っているように思えますが、落とし穴も存在します。これを「次元の呪い」と言い、データの次元、つまり情報の種類が増えるほど、解析が難しくなる現象を指します。この問題に対処するには、データの性質を深く理解し、適切に準備することが非常に大切です。
まず、データがどのように分布しているのか、それぞれの情報がどのように関係しているのかを詳しく調べることが必要です。どの情報が結果に大きく影響し、どの情報が不要なノイズなのかを見極めることで、解析の効率を高めることができます。
次に、集めたデータを解析に適した形に整える「前処理」も重要です。例えば、情報の種類ごとに単位や範囲が異なる場合、数値を揃える処理が必要です。これをしないと、特定の情報の影響が過大に評価されてしまう可能性があります。また、欠けている情報や極端に大きい、あるいは小さい値は、解析結果を歪める原因となるため、適切に処理しなければなりません。具体的には、平均値で補完したり、異常値を取り除いたりするなどの方法があります。
データの理解と準備を怠ると、「次元の呪い」の影響をより強く受けてしまうため、慎重に進める必要があります。例えば、データ全体の様子を視覚的に把握できる図表作成ツールなどを活用すると、データの性質を理解しやすくなります。情報の関係性を図示することで、隠れた規則性や異常値を発見できる可能性が高まります。適切な準備と解析を行うことで、高次元データに潜む価値を引き出し、より良い結論を導き出すことができます。