残差平方和:モデル評価の基礎

AIを知りたい
先生、『SSE』ってなんですか?よく分かりません。

AIエンジニア
『SSE』は『残差平方和』のことで、機械学習モデルの予測がどれだけ実際の値からずれているかを測る指標の一つだよ。モデルの予測値と実際の値の差を『残差』というんだけど、その残差を二乗して、全部足し合わせたものがSSEなんだ。

AIを知りたい
残差を二乗するのはなぜですか?そのまま足し合わせたらダメなんですか?

AIエンジニア
いい質問だね。残差をそのまま足し合わせると、正の値と負の値が打ち消しあって、ずれの大きさが正しく測れないんだ。だから、二乗してすべて正の値にすることで、ずれの大きさを正しく反映できるんだよ。ちなみに、残差の計算は「観測値−予測値」でも「予測値−観測値」でも、二乗すれば結果は同じになるよ。
SSEとは。
人工知能の分野でよく使われる言葉「SSE」について説明します。SSEとは、統計学や機械学習で使われるもので、残差の平方和を計算して、その合計値を出すためのものです。残差とは、実際の値と予想した値の差のことです。ちなみに、残差を計算するとき、実際の値から予想値を引いても、予想値から実際の値を引いても、SSEの値は変わりません。
残差平方和とは

統計や機械学習の世界では、予測モデルの良し悪しを測ることはとても大切です。そのために、「残差平方和」という尺度がよく使われます。これは、簡単に言うと、モデルがどれくらい実際のデータに合っているかを表す数値です。
例えば、来月の商品の売上を予測するモデルを作ったとします。このモデルを使って予測した売上と、実際に来月売れた商品の売上には、当然ながら差が出てきます。この差のことを「残差」と言います。残差が小さいということは、予測が実際の値に近かったということなので、良いモデルと言えます。逆に、残差が大きいと、予測が外れてしまったということなので、モデルの精度が低いと言えます。
残差平方和は、この残差を二乗して、全てのデータについて足し合わせたものです。二乗する理由は、残差にはプラスとマイナスがあるので、そのまま足し合わせると、互いに打ち消しあってしまい、全体の誤差が正しく評価できないからです。二乗することで、全ての残差をプラスの値に変換し、合計することで全体の誤差を適切に測ることができます。
残差平方和の値が小さいほど、モデルの予測精度が高いと言えます。これは、残差が小さい値ばかりであれば、二乗して足し合わせても小さな値になるからです。逆に、残差平方和の値が大きい場合は、モデルの予測精度が低いということになります。
残差平方和は、モデルの精度を評価するための重要な指標であり、より良い予測モデルを作る上で欠かせないものです。様々な場面で使われているので、理解しておくと役に立ちます。
| 用語 | 説明 |
|---|---|
| 残差 | 予測値と実測値の差 |
| 残差平方和 | 全てのデータの残差を二乗し、合計した値 |
| 残差平方和の値が小さい | 予測精度が高い |
| 残差平方和の値が大きい | 予測精度が低い |
| 二乗する理由 | 残差のプラスとマイナスを打ち消し合わないようにするため |
計算方法と注意点

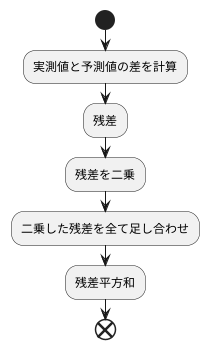
残差平方和は、統計学において、データと予測モデルのずれの大きさを測る指標です。その計算方法は比較的簡単で、いくつかの手順を踏むことで求めることができます。まず、それぞれのデータ点において、実際に観測された値とモデルによって予測された値の差を計算します。この差を残差と呼びます。残差は、モデルがどれだけデータの動きを捉えきれていないかを表す値です。次に、計算したそれぞれの残差を二乗します。二乗することで、残差が正負どちらの値であっても正の値に変換され、ずれの大きさのみを評価できます。そして最後に、二乗した残差を全て足し合わせます。この合計値が残差平方和であり、モデルとデータ全体のずれの大きさを示します。
残差を計算する際、「実測値から予測値を引く」か「予測値から実測値を引く」かという二つの計算順序が考えられます。どちらの順序で計算しても、最終的な残差平方和の値は変わりません。これは、二乗の計算によって残差の符号が打ち消されるためです。しかし、残差そのものの意味は異なります。「実測値から予測値を引く」場合は、実測値を基準としてどれだけ予測値がずれているかを表し、「予測値から実測値を引く」場合は、予測値を基準としてどれだけ実測値がずれているかを表します。どちらの順序で計算するかは、モデルの評価方法や解釈の目的に合わせて適切に選択することが大切です。
残差平方和はデータの量に影響を受けやすいという性質があります。データの数が多いほど、残差平方和は大きくなる傾向があります。そのため、異なるデータの集団を比べる際には、残差平方和をそのまま使うのではなく、データの数などを考慮した相対的な指標を用いるなどの工夫が必要です。例えば、残差平方和をデータの数で割った平均平方和などが用いられます。
モデル評価における役割

予測モデルの良し悪しを測ることは、モデルを作る上でとても大切な仕事です。作ったモデルがどれくらい使えるものなのかをきちんと調べなければ、そのモデルを使って将来を予測したり、より良いものを選んだりすることができません。モデルの評価には様々な方法がありますが、その中でも「残差平方和」、略して「残差二乗和」と呼ばれるものは、基本となる大切な指標の一つです。
残差二乗和とは、簡単に言うと、モデルがどれくらいデータとずれているかを表す数値です。例えば、ある商品の来月の売上を予測するモデルを作ったとします。このモデルを使って予測した売上と、実際に来月になった時の本当の売上の差が「残差」です。この残差を二乗して、全てのデータについて足し合わせたものが残差二乗和です。当然、残差二乗和が小さければ小さいほど、モデルの予測は実際の値に近く、良いモデルと言えるでしょう。
しかし、残差二乗和だけでモデルの全てを判断してはいけません。落とし穴があるのです。例えば、扱うデータの数が多かったり、予測に使う要素の数が多いほど、残差二乗和は大きくなる傾向があります。これは、データや要素が増えるほど、モデルが複雑になり、予測のずれも大きくなりやすいためです。ですから、残差二乗和だけでモデルを比べるのは、異なる大きさのものさしで長さを比べるようなものなのです。
より正確にモデルを評価するためには、残差二乗和だけでなく、他の指標も合わせて見る必要があります。「決定係数」は、モデルがどれくらいデータのばらつきを説明できているかを表す指標で、値が1に近いほど、モデルはデータをよく説明できていると言えます。また、「平均二乗誤差」は、残差二乗和をデータの数で割ったもので、データの量の影響を取り除いた指標です。これらの指標を組み合わせて使うことで、モデルの良さ悪しを多角的に判断し、本当に使える良いモデルを選ぶことができるのです。
| 指標名 | 説明 | 備考 |
|---|---|---|
| 残差二乗和 (残差平方和) | モデルの予測値と実際の値のずれ(残差)を二乗し、合計した値。モデルの予測精度を示す。 | 値が小さいほど良いモデル。ただし、データ量や予測要素の数に影響されるため、単独での比較は不適切。 |
| 決定係数 | モデルがデータのばらつきをどれくらい説明できているかを表す指標。 | 値が1に近いほど、モデルはデータをよく説明できている。 |
| 平均二乗誤差 | 残差二乗和をデータの数で割った値。データ量の影響を取り除いた指標。 | 値が小さいほど良いモデル。 |
他の指標との関係

残差平方和(ざんさへいほうわ)は、統計の世界でモデルの良し悪しを測るための大切な道具であり、他の様々な指標と深い関わりを持っています。このため、残差平方和を理解することは、統計モデルを扱う上で非常に重要です。残差平方和とは、モデルによる予測値と実際の値との差、つまり残差をそれぞれ二乗して合計した値です。この値が小さいほど、モデルの予測が実際の値に近いことを示しています。
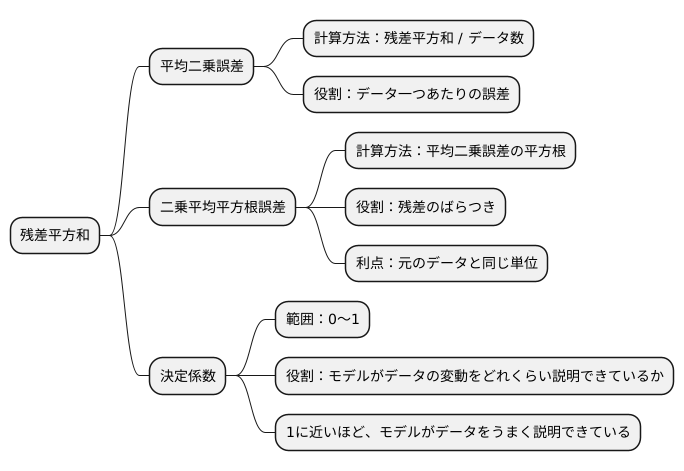
まず、平均二乗誤差(へいきんじじょうごさ)を見てみましょう。これは、残差平方和をデータの数で割った値です。平均二乗誤差は、残差の二乗の平均を表すため、データ一つあたりどれくらいの誤差があるのかを把握するのに役立ちます。残差平方和は全体の誤差を表すのに対し、平均二乗誤差は一つあたりの誤差を表すという違いがあります。
次に、二乗平均平方根誤差(にじょうへいきんへいほうこんごさ)について説明します。これは、平均二乗誤差の平方根をとった値であり、残差のばらつきの程度を示す指標です。二乗平均平方根誤差は、元のデータと同じ単位を持つため、誤差の大きさを直感的に理解しやすいという利点があります。
さらに、決定係数(けっていけいすう)も残差平方和と関連しています。決定係数は、モデルがデータの変動をどれくらい説明できているかを表す指標で、0から1までの値をとります。1に近いほど、モデルがデータをうまく説明できていることを示します。決定係数の計算にも残差平方和が利用されており、モデルの全体的な性能を評価する上で重要な役割を果たしています。
このように、残差平方和は、平均二乗誤差、二乗平均平方根誤差、決定係数といった他の指標の計算に用いられる基盤となる重要な指標です。これらの指標を理解することで、統計モデルの精度をより深く評価し、より良いモデルを選択することが可能になります。
応用例と活用

残差平方和は、様々な分野で活用されている重要な指標です。これは、予測モデルと実際のデータとのずれを数値化したものと言えます。このずれが小さいほど、モデルの予測精度が高いと判断できます。
経済学の分野では、例えば消費者の購買行動を予測する需要予測モデルを作る際に、残差平方和が役立ちます。モデルが算出した予測値と、実際の購買データとの差を平方和として計算することで、モデルの精度を測ることができます。残差平方和が小さいほど、需要予測モデルの精度が高いことを示し、企業はより正確な生産計画や在庫管理を行うことができます。
金融工学においても、残差平方和は重要な役割を果たします。株価の変動を予測するモデルを構築する際に、過去の株価データを用いてモデルを学習させます。この際、残差平方和を最小化するようにモデルのパラメータを調整することで、将来の株価をより正確に予測できるモデルを作ることができます。
医療の分野では、病気の診断や治療効果の予測に活用されています。例えば、患者の症状や検査データから病気を診断するモデルを開発する際に、残差平方和を用いてモデルの精度を評価します。また、ある治療法の効果を予測するモデルにおいても、残差平方和を用いることで、治療効果の予測精度を上げることができます。
このように、残差平方和は経済学、金融工学、医療といった分野だけでなく、販売促進のための市場分析や、スポーツ選手の成績予測など、様々な分野で広く活用されています。データに基づいてより良い意思決定を行うために、残差平方和はなくてはならない指標となっています。
| 分野 | 活用例 |
|---|---|
| 経済学 | 需要予測モデルによる消費者の購買行動予測、生産計画、在庫管理 |
| 金融工学 | 株価変動予測モデル構築、将来株価予測 |
| 医療 | 病気の診断、治療効果予測 |
| その他 | 市場分析、スポーツ選手の成績予測 |
まとめ

まとめとして、残差平方和(以下、残差二乗和)について改めて考えてみましょう。残差二乗和は、統計学や機械学習といった分野で、モデルの予測精度を測る基本的な指標として広く使われています。
残差二乗和とは、実際の測定値とモデルが予測した値との差を二乗して、すべて足し合わせたものです。この値が小さいほど、モデルの予測が実際の値に近い、つまり予測精度が高いことを示します。計算方法は単純で、実際の値と予測値の差をそれぞれ二乗し、その合計を求めるだけです。比較的簡単な計算で求めることができます。
しかし、扱うデータの量によって、残差二乗和の値も大きくなってしまうという性質があります。例えば、データ数が少ない場合と多い場合では、たとえ予測精度が同じでも、データ数が多い方が残差二乗和は大きくなってしまいます。そのため、残差二乗和だけでモデルの良し悪しを判断するのではなく、他の指標も組み合わせて総合的に判断することが大切です。
残差二乗和は、平均二乗誤差や決定係数といった他の指標とも深い関わりがあります。これらの指標もモデルの精度を評価するために使われるもので、残差二乗和と合わせて見ることで、より多角的にモデルを評価することができます。
様々な分野で、モデルの評価に残差二乗和は役立っています。残差二乗和を正しく理解し、適切に使うことで、データ分析の精度を高めることができます。そして、その結果に基づいて、より良い決定を下したり、問題を解決したりすることに繋がるのです。
| 項目 | 説明 |
|---|---|
| 残差二乗和の定義 | 実際の測定値とモデルが予測した値との差を二乗して、すべて足し合わせたもの |
| 値の意味 | 小さいほど、モデルの予測精度が高い |
| 計算方法 | 実際の値と予測値の差をそれぞれ二乗し、その合計を求める |
| 注意点 | データ量が多いほど値が大きくなるため、他の指標と組み合わせて総合的に判断する必要がある |
| 関連指標 | 平均二乗誤差、決定係数 |
| 利点 | 様々な分野でモデル評価に役立ち、データ分析の精度向上に貢献 |
