二乗和誤差:機械学習の基本概念

AIを知りたい
先生、「二乗和誤差」って、よく聞くんですけど、具体的にどういう意味ですか?

AIエンジニア
そうだね。「二乗和誤差」は、機械学習で予測した値と実際の値がどれくらい離れているかを測る尺度の一つだよ。それぞれの予測値と実際の値の差を二乗して、全部足し合わせたものなんだ。

AIを知りたい
実際の値との差を二乗するのはなぜですか?

AIエンジニア
いい質問だね。差をそのまま足し合わせると、プラスとマイナスが打ち消し合ってしまうことがある。二乗することで、常に正の値になり、誤差の大きさを正しく反映できるんだ。それに、大きな誤差をより強調する効果もあるんだよ。
二乗和誤差とは。
人工知能で使われる言葉の一つに「二乗和誤差」というものがあります。これは統計学や機械学習で使われ、実際の値と予測した値の差をそれぞれ二乗して、すべて足し合わせたものです。ちなみに、実際の値から予測値を引いても、予測値から実際の値を引いても、計算結果は変わりません。
二乗和誤差とは

二乗和誤差とは、機械学習の分野で、モデルの良し悪しを測る物差しの一つです。作ったモデルが、どれくらい実際の値に近い予測をしているのかを確かめるために使われます。
具体的には、まずモデルを使って値を予測します。そして、その予測値と実際に観測された値との差を計算します。この差のことを「残差」と言います。この残差が小さいほど、予測が実際の値に近かったと言えるでしょう。しかし、残差には正の値も負の値もあります。そのまま全部足してしまうと、互いに打ち消し合ってしまい、正確な評価ができません。そこで、それぞれの残差を二乗します。二乗することで、全ての値が正になり、打ち消し合いの問題を避けることができます。そして、これらの二乗した残差を全て合計したものが、二乗和誤差です。
例えば、商品の売上の予測モデルを考えてみましょう。モデルが10個売れると予測し、実際には8個売れたとします。この時の残差は2です。別の商品では、モデルが5個売れると予測し、実際には7個売れたとします。この時の残差は-2です。これらの残差をそれぞれ二乗すると、4と4になります。これらの二乗した残差を合計することで、二乗和誤差を計算できます。
二乗和誤差は、値が小さいほど、モデルの予測精度が高いと言えます。つまり、モデルの予測値と実際の値とのずれが小さいことを意味するからです。逆に、二乗和誤差が大きい場合は、モデルの予測精度が低いと考えられ、モデルの改良が必要となります。このように、二乗和誤差は、モデルの性能を分かりやすく示してくれるため、広く使われています。
| 用語 | 説明 |
|---|---|
| 二乗和誤差 | 機械学習モデルの予測精度を評価するための指標。モデルの予測値と実際の値の差(残差)を二乗し、それらを合計した値。値が小さいほど予測精度が高い。 |
| 残差 | モデルの予測値と実際の値の差。 |
| 計算方法 | 1. 予測値と実測値の差(残差)を計算する。 2. 各残差を二乗する。 3. 全ての二乗した残差を合計する。 |
| 例 | 予測値10, 実測値8 -> 残差2 -> 二乗値4 予測値5, 実測値7 -> 残差-2 -> 二乗値4 二乗和誤差 = 4 + 4 = 8 |
| 評価 | 二乗和誤差が小さいほど、モデルの予測精度が高い。 |
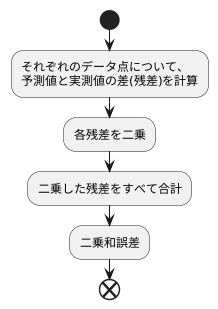
計算方法

二乗和誤差は、様々な分野で予測の精度を評価する際に広く使われている指標です。この誤差は、モデルの予測値と実際の観測値とのずれの大きさを示すものです。計算方法は非常に分かりやすく、いくつかの手順を踏むことで簡単に求めることができます。
まず、それぞれのデータ点について、モデルが予測した値と実際に観測された値の差を計算します。この差は、予測がどれだけ観測値から離れているかを示すもので、残差とも呼ばれます。例えば、ある商品の売上予測モデルで、今日の売上が100個と予測され、実際の売上個数が120個だった場合、残差は120 – 100 = 20となります。
次に、計算したそれぞれの残差を二乗します。二乗する理由は、残差に正負の値が混在している場合、単純に合計すると値が相殺されてしまうためです。二乗することで、全ての残差を正の値に変換し、誤差の大きさを適切に反映させることができます。先ほどの例でいえば、残差20を二乗すると400となります。
最後に、二乗した残差を全て合計します。これが二乗和誤差です。データ点が10個ある場合、10個の残差をそれぞれ二乗し、その合計値が二乗和誤差となります。例えば、10個の二乗した残差がそれぞれ1、4、9、16、25、36、49、64、81、100だとすると、二乗和誤差はこれらの合計値である385となります。このようにして計算された二乗和誤差は、値が小さいほど予測精度が高いことを示します。つまり、二乗和誤差が0に近いほど、モデルの予測値が観測値によく合致していると言えるのです。
これらの計算は、計算機や表計算ソフトを用いることで容易に実行できます。大量のデータに対しても、数式を一度入力すれば自動的に計算してくれるため、非常に便利です。
残差の順番

誤差を測る尺度の一つに、二乗和誤差というものがあります。これは、観測された値と予測した値の差、つまり残差を二乗した合計を計算することで得られます。この残差の計算について、「観測値から予測値を引く」場合と「予測値から観測値を引く」場合で、結果に違いが生じるのではないかと疑問に思う方もいるかもしれません。しかし、どちらの順番で計算しても、最終的な二乗和誤差は変わりません。
具体的に考えてみましょう。例えば、商品の売れた個数を予測するモデルを作ったとします。ある日の実際の売上個数が5個で、モデルが予測した売上個数が3個だったとしましょう。この時、「観測値ー予測値」の順番で計算すると、5ひく3で2となります。この2を二乗すると4です。次に順番を逆に、「予測値ー観測値」で計算してみます。3ひく5はマイナス2です。マイナス2を二乗すると、やはり4になります。このように、残差の計算の順番を変えても、二乗した結果には影響がありません。
これは、二乗するという計算の性質によるものです。マイナスの数を二乗するとプラスになるため、残差の符号の違いは二乗によって打ち消されてしまいます。つまり、二乗和誤差は、残差のプラス、マイナスといった方向ではなく、予測値と観測値のずれの大きさのみを重視していると言えるでしょう。
したがって、二乗和誤差を計算する上では、残差の計算順序はどちらでも構いません。計算しやすいと感じる方を選んで計算すれば問題ありません。重要なのは、予測値と観測値がどれくらい離れているか、そのずれの大きさを把握することです。そして、そのずれを最小にするようにモデルを調整していくことが、予測精度を高めるための重要な一歩となります。
| 計算方法 | 式 | 結果 | 二乗結果 |
|---|---|---|---|
| 観測値 – 予測値 | 5 – 3 = 2 | 2 | 4 |
| 予測値 – 観測値 | 3 – 5 = -2 | -2 | 4 |
応用例

二乗和誤差は、様々な計算方法で使われる大切な考え方です。特に、機械学習の分野では、予測と実際の値のずれを測る基本的な方法として使われています。
例えば、線形回帰という計算方法を考えてみましょう。線形回帰は、データの散らばりを表す直線を引く方法です。この直線は、データの点と直線の距離の二乗を合計した値、つまり二乗和誤差が最も小さくなるように決められます。二乗和誤差を使うことで、データに最もよく合う直線を簡単に計算することができます。
また、近年注目されているニューラルネットワークのような複雑な計算方法でも、二乗和誤差は重要な役割を担っています。ニューラルネットワークは、人間の脳の仕組みを真似た複雑な繋がりを持った計算モデルです。このモデルの学習、つまりモデルがうまく予測できるようにするための調整過程で、二乗和誤差が指標として使われます。具体的には、予測値と実際の値の二乗和誤差を計算し、この誤差が小さくなるようにモデルのパラメータと呼ばれる数値を調整していきます。
さらに、二乗和誤差は、学習済みのモデルの性能を評価する際にも使われます。モデルの性能評価とは、未知のデータに対してどれだけ正確に予測できるかを調べることです。学習に使ったデータと、学習に使っていないデータでそれぞれ二乗和誤差を計算し、その値を比較することで、モデルがどれだけ汎化性能を持っているか、つまり未知のデータにも対応できるかを評価することができます。もし、学習に使ったデータの二乗和誤差が小さくても、学習に使っていないデータの二乗和誤差が大きい場合は、そのモデルは学習データだけに特化してしまい、新しいデータには対応できないことを意味します。このように、二乗和誤差はモデルの汎化性能を評価するための重要な指標となっています。
| 分野 | 利用方法 | 詳細 |
|---|---|---|
| 機械学習 | 予測と実測値のずれの測定 | 基本的な方法として使用 |
| 線形回帰 | データに最適な直線の決定 | データ点と直線の距離の二乗和を最小化 |
| ニューラルネットワーク | モデル学習の指標 | 予測値と実測値の二乗和誤差を最小化 |
| モデル性能評価 | 汎化性能の評価 | 学習データと未学習データの二乗和誤差を比較 |
他の指標との関係

機械学習の模型の良し悪しを測る尺度は、二乗和誤差以外にもたくさんあります。それぞれの尺度は異なる側面から模型の性能を評価するため、目的に合わせて適切な尺度を選ぶことが大切です。二乗和誤差は、これらの尺度の基礎となる重要な考え方であり、機械学習を学ぶ上で欠かせません。
まず、平均二乗誤差について説明します。これは、二乗和誤差をデータの個数で割った値です。二乗和誤差と同様に、模型がどれくらい正確に予測できているかを評価するために使われます。データの個数で割ることで、データの量に左右されずに模型の性能を比較することができます。
次に、二乗平均平方根誤差について説明します。これは、平均二乗誤差の平方根をとった値です。平方根をとることで、元のデータと同じ単位で誤差を表現できるため、理解しやすくなります。例えば、元のデータが長さの単位で測られている場合、二乗平均平方根誤差も長さの単位で表されます。これにより、誤差の大きさを直感的に把握することができます。
さらに、決定係数という尺度もあります。これは、模型がデータの変化をどれくらい説明できているかを表す尺度です。0から1までの値をとり、1に近いほど模型がデータをよく説明できていることを示します。具体的には、データ全体の変化のうち、模型によって説明できる変化の割合を表しています。決定係数は、模型の予測精度だけでなく、データへの適合度も評価できる点で有用です。
このように、二乗和誤差以外にも様々な尺度が存在し、それぞれ異なる情報を提供してくれます。これらの尺度を理解し、適切に使い分けることで、より効果的に機械学習模型を評価し、改善していくことができます。
| 尺度名 | 説明 | 特徴 |
|---|---|---|
| 平均二乗誤差 | 二乗和誤差をデータの個数で割った値 | データの量に左右されずに模型の性能を比較できる |
| 二乗平均平方根誤差 | 平均二乗誤差の平方根をとった値 | 元のデータと同じ単位で誤差を表現できるため、理解しやすい |
| 決定係数 | 模型がデータの変化をどれくらい説明できているかを表す尺度 | 0から1までの値をとり、1に近いほど模型がデータをよく説明できている |
限界

広く使われている予測の正確さを測る方法の一つに、二乗和誤差というものがあります。これは、実際の値と予測値の差を二乗し、その合計を求めることで計算されます。しかし、この方法には弱点があります。それは、極端に外れた値、いわゆる外れ値の影響を受けやすいということです。
たとえば、ほとんどのデータが予測値とほぼ一致し、差がほとんどない場合でも、一つだけ大きく外れたデータがあると、その差が二乗されることで、全体の誤差が非常に大きくなってしまうのです。具体的な例を挙げると、10個のデータのうち9個の差が1だったとしても、残りの1つの差が10だった場合、その1つだけのデータのために誤差が大きく膨らんでしまいます。9個のデータの差の二乗の合計は9ですが、外れ値の差の二乗は100となり、全体の二乗和誤差は109となります。つまり、大部分のデータが予測値に近い場合でも、たった一つの外れ値によって、モデルの評価が大きく歪められてしまう可能性があるのです。
このような外れ値の影響を軽減する方法としては、大きく外れたデータを分析から除外する方法や、二乗和誤差とは異なる指標を用いる方法が考えられます。たとえば、差の絶対値の合計を用いる平均絶対誤差は、外れ値の影響を受けにくい指標として知られています。それぞれの指標には長所と短所があります。ですから、データの特性や分析の目的に合わせて、適切な指標を選ぶことが重要になります。どの指標を使うかによって、モデルの評価結果が大きく変わる可能性があるため、慎重に検討する必要があります。
| 指標 | 計算方法 | 外れ値の影響 | 長所 | 短所 |
|---|---|---|---|---|
| 二乗和誤差 | 実際の値と予測値の差を二乗し、その合計を求める。 | 影響を受けやすい | 計算が容易 | 外れ値の影響を受けやすい |
| 平均絶対誤差 | 差の絶対値の合計を用いる。 | 影響を受けにくい | 外れ値の影響を受けにくい | 二乗和誤差と比べて計算が複雑 |
