単純パーセプトロン:機械学習の基礎

AIを知りたい
単純パーセプトロンって、たくさんの入力があって、それぞれに重みづけがされて、最後に一つの出力になるんですよね?でも、その重みづけって、どうやって決めるんですか?

AIエンジニア
良い質問ですね。重みづけは、最初はランダムに決めます。そして、出力値と正解を見比べて、重みを少しずつ調整していくんです。

AIを知りたい
少しずつ調整する?どういうことですか?

AIエンジニア
例えば、出力が大きすぎた場合は、その出力に繋がっている入力の重みを小さくします。逆に小さすぎた場合は、重みを大きくします。これを何度も繰り返すことで、正解に近い出力をするように重みを調整していくんです。この調整方法を学習と言います。
単純パーセプトロンとは。
人工知能の用語で『単純パーセプトロン』というものがあります。これは、人の脳にある神経細胞の仕組みをまねて作った、簡単な模型のことです。いくつかの入力それぞれに重みづけをして、最後に一つの値を出力します。
単純パーセプトロンとは

単純パーセプトロンとは、機械学習の初期に登場した最も基本的な脳の仕組みを模した数理モデルです。人間の脳は、無数の神経細胞(ニューロン)が複雑に繋がり、情報を処理することで様々な機能を実現しています。このニューロンの働きを単純化したものが、単純パーセプトロンです。
単純パーセプトロンは、複数の入力信号を受け取ります。例えば、ある画像が猫かどうかを判断する場合、画像の明るさ、色、形といった様々な特徴が入力信号となります。これらの入力信号は、それぞれ異なる重要度を持つと考えられます。そこで、単純パーセプトロンでは、各入力信号に重みと呼ばれる数値を割り当て、重要度を表現します。重みが大きいほど、その入力信号は出力に大きな影響を与えます。
単純パーセプトロンは、入力信号と重みを掛け合わせた値を全て足し合わせ、その合計値がある値(しきい値)を超えた場合に「1」、超えなかった場合に「0」を出力します。例えば、猫の画像を入力した場合、猫の特徴に合致する入力信号の重みが大きいため、合計値がしきい値を超え、「1」(猫である)と出力されます。一方、猫ではない画像を入力した場合は、合計値がしきい値を超えず、「0」(猫ではない)と出力されます。
単純パーセプトロンは、学習を通じて重みを調整することで、より正確な判断を行うことができます。最初はランダムに設定された重みを、入力データと正解データを使って徐々に修正していくことで、特定のパターンを認識する能力を獲得します。このように、単純パーセプトロンは、複雑な脳の機能を理解する手がかりとなるだけでなく、現代の人工知能技術の基礎としても重要な役割を果たしています。
仕組みと動作原理

単純パーセプトロンは、人間の脳神経細胞の働きをまねて作られたものです。人間の脳は、無数の神経細胞が複雑につながり合って情報を処理していますが、単純パーセプトロンはこの神経細胞の働きをとても簡単に表したものです。
複数の入り口からの信号は、それぞれ異なる重みをつけてパーセプトロンに送られます。これは、神経細胞のつながりの強さを表す「シナプス」の働きに似ています。それぞれの入り口からの信号は、この重みに掛け算されて、パーセプトロンに送られます。パーセプトロンの中では、これらの重みを掛けた信号をすべて足し合わせます。
この足し合わせた値がある基準値を超えると、パーセプトロンは「1」という信号を出力します。逆に、基準値を超えない場合は「0」を出力します。この基準値のことを「閾値」といいます。この閾値は、パーセプトロンが反応するかどうかを決める大切な値です。まるで、コップに水を注ぎ続けると、ある水位を超えた時に水が溢れ出すようなものです。閾値は、ちょうどその水位に当たるといえます。
例えば、猫の絵を見分ける場合を考えてみましょう。絵のそれぞれの小さな点は、パーセプトロンへの入り口からの信号になります。それぞれの点は、猫の特徴を表す度合いによって、異なる重みを持ちます。例えば、猫の耳の形に似た点には大きな重みがつけられ、背景の部分の点には小さな重みがつけられます。パーセプトロンは、これらの重みを掛けた点の明るさの値をすべて足し合わせます。そして、その合計値が閾値を超えれば、「これは猫の絵だ」と判断し、「1」を出力します。もし閾値を超えなければ、「猫の絵ではない」と判断し、「0」を出力します。
このように、単純パーセプトロンは、入り口からの信号、重み、そして閾値という簡単な仕組みにより、複雑な判断を下すことができます。これは、人間の脳の働きを単純化したモデルですが、機械学習の基礎となる重要な考え方です。
学習方法

学習方法は、適切な値を見つけ出すための手順です。この手順では、たくさんの例題とそれぞれの正解を使って、試行錯誤を繰り返しながら、より良い結果を出せるように調整していきます。
具体的には、「教師あり学習」という方法を使います。これは、先生のように正解を教えてもらいながら学ぶ方法です。たくさんの例題と、それぞれの例題に対する正解を用意します。そして、現在の値を使って例題を試してみて、その結果と正解を比べます。もし結果が正解と違っていたら、値を少しだけ変えて、正解に近づくように調整します。
この調整を何度も繰り返すことで、次第に正解に近い結果を出せるようになります。ちょうど、子供の頃、何度も練習して自転車に乗れるようになったのと同じです。最初はうまくバランスが取れなくても、練習を続けることで、次第に上手に乗れるようになります。
例えば、猫の絵を見分ける場合を考えてみましょう。たくさんの猫の絵と「これは猫です」という正解、そして猫ではない絵と「これは猫ではありません」という正解をたくさん用意します。そして、現在の値を使って、それぞれの絵が猫かどうかを判断させます。もし間違えていたら、値を調整して、猫の絵は「猫」と正しく判断できるように、猫ではない絵は「猫ではない」と正しく判断できるように調整します。
この学習を繰り返すことで、猫の特徴を捉える値が自然と調整され、最終的には高い精度で猫の絵を見分けられるようになります。まるで、たくさんの猫の絵を見て、猫の特徴を覚えるのと同じです。最初は猫の特徴がよく分からなくても、たくさんの猫の絵を見ることで、次第に猫の特徴を理解し、猫を見分けられるようになります。
| 学習方法 | 教師あり学習 | 例:猫の絵を見分ける |
|---|---|---|
| 手順 | たくさんの例題とそれぞれの正解を使って、試行錯誤を繰り返す。値を調整して、より良い結果を出せるようにする。 | 猫の絵と「これは猫です」という正解、猫ではない絵と「これは猫ではありません」という正解をたくさん用意。それぞれの絵が猫かどうかを判断させ、間違えていたら値を調整。 |
| 具体例 | 自転車の練習。最初はうまくいかないが、練習を続けることで上手に乗れるようになる。 | たくさんの猫の絵を見て、猫の特徴を覚える。最初は分からなくても、たくさん見ることで、猫の特徴を理解し、見分けられるようになる。 |
限界と発展

単純パーセプトロンは、人工知能の分野に革新をもたらした画期的な学習モデルです。これは、人間の脳神経細胞の働きを模倣したシンプルな仕組みで、入力データに対して重み付けを行い、その合計値がある閾値を超えた場合にのみ出力を出すというものです。この仕組みによって、様々な種類のデータを分類することが可能になりました。例えば、画像認識においては、画像に含まれる特徴を数値化し、その数値に基づいて画像がどのカテゴリーに属するのかを判断することができます。しかし、単純パーセプトロンには、線形分離可能な問題しか扱えないという大きな限界がありました。線形分離可能とは、データの集合を一本の直線で完全に区切ることができるという意味です。例えば、リンゴとミカンを大きさで分類する場合、ある大きさよりも大きいものをリンゴ、小さいものをミカンとすれば、一本の直線で分類できます。しかし、排他的論理和(XOR)のような複雑な問題では、データを一本の直線で分類することができません。このような非線形な問題は、単純パーセプトロンでは正しく学習することができず、その適用範囲は限定的でした。
この限界を克服するために、研究者たちは多層パーセプトロンという新しいモデルを開発しました。これは、複数の単純パーセプトロンを層状に組み合わせたもので、それぞれの層が前の層の出力を入力として受け取り、次の層に出力するという構造になっています。この多層構造によって、非線形な問題も学習できるようになりました。イメージとしては、複数の直線を組み合わせて複雑な図形を描くようなものです。それぞれの直線は単純な分類しかできませんが、それらを組み合わせることで複雑な分類が可能になります。さらに、多層パーセプトロンは、入力データの特徴を自動的に学習する能力も備えており、より高度な問題解決に役立ちます。
単純パーセプトロンは、それ自体では限界がありましたが、多層パーセプトロンをはじめとする、より複雑なニューラルネットワークモデルの基礎となる重要な概念を提供しました。現代の深層学習技術も、この単純パーセプトロンの概念を拡張したものであり、その影響は人工知能の発展に計り知れないものがあります。現在、深層学習は画像認識、音声認識、自然言語処理など様々な分野で活用されており、私たちの生活をより豊かにするために日々進化を続けています。
| モデル | 仕組み | 能力 | 限界 |
|---|---|---|---|
| 単純パーセプトロン | 入力データに重み付けを行い、合計値がある閾値を超えた場合のみ出力 | 線形分離可能な問題の分類 | 線形分離不可能な問題(例: XOR)は扱えない |
| 多層パーセプトロン | 複数の単純パーセプトロンを層状に組み合わせ、各層が前の層の出力を入力として受け取り、次の層に出力 | 非線形な問題も学習可能、入力データの特徴を自動的に学習 | – |
応用例

単純パーセプトロンは、簡単な仕組みでありながら、幅広い分野で使われています。その分かりやすさから、様々な応用が考えられています。
まず、文字や画像、音声といった模様を見分ける技術に活用できます。例えば、手書きの文字を認識したり、写真に写っている物体を判別したり、音声データから言葉を聞き分けたりするといった場面で使われています。単純パーセプトロンは、このようなパターン認識の基礎となる分類作業を担います。
医療の分野でも、単純パーセプトロンは活躍しています。例えば、患者の症状から病気を診断する支援システムに利用されています。また、金融の分野では、株価の変動予測や融資の審査など、様々な場面で意思決定を支援するシステムに組み込まれています。
近年は、より複雑で高性能な深層学習が登場し、単純パーセプトロン単体で用いられる機会は少なくなってきました。しかし、単純パーセプトロンの考え方は、深層学習をはじめとする様々な人工知能技術の土台となっています。複雑なニューラルネットワークの仕組みを理解するためには、まず単純パーセプトロンの仕組みを理解することが重要です。
単純パーセプトロンを学ぶことは、人工知能の基礎を理解する上で非常に大切です。人工知能技術の進歩を理解し、将来の技術革新を予測するためにも、単純パーセプトロンの理解は欠かせません。単純パーセプトロンは、現代の人工知能技術の礎を築いた重要な技術と言えるでしょう。
| 分野 | 応用例 |
|---|---|
| パターン認識 | 文字認識、画像認識、音声認識 |
| 医療 | 病気診断支援 |
| 金融 | 株価変動予測、融資審査 |
| 人工知能の基礎 | 深層学習の理解に重要 |
今後の展望

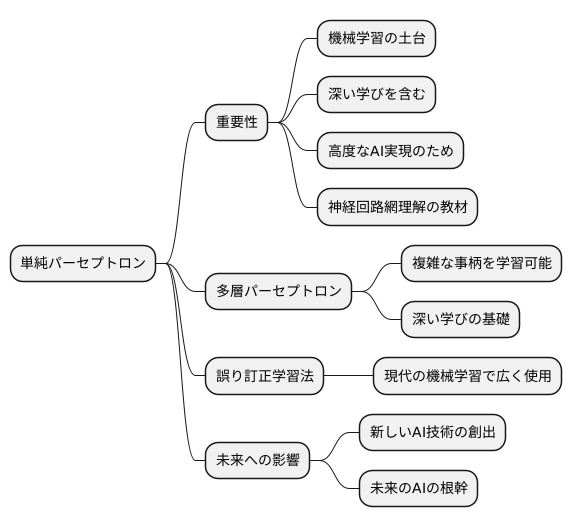
単純パーセプトロンは、今では少し古い学習の仕組みと考えられていますが、その基本となる考え方は、今の時代の深い学びを含む、色々な機械学習の仕組みの土台となっています。これから、もっと複雑になる資料の分析や、高いレベルの知能を持つ機械を実現するために、単純パーセプトロンを理解することは、ますます大切になっていくでしょう。
特に、神経回路網がどのように動くのか、どのように学ぶのかを理解する上で、単純パーセプトロンは最高の教材です。複雑な神経回路網も、基本は単純パーセプトロンの組み合わせでできています。単純パーセプトロンを学ぶことで、複雑な神経回路網のモデルがどのように動くのかを、より深く理解することができます。そして、新しい人工知能の技術を生み出すことにも繋がるでしょう。
例えば、たくさんの単純パーセプトロンを繋げて層状にすると、多層パーセプトロンと呼ばれる、より複雑な事柄を学習できるようになります。これは、今の深い学びの基礎となっています。また、単純パーセプトロンの学習方法である誤り訂正学習法は、今の機械学習でも広く使われています。このように、単純パーセプトロンは、現代の機械学習の様々な部分で、重要な役割を担っています。
これから先、もっとすごい人工知能が出てきたとしても、その根っこには、単純パーセプトロンの考え方が生きているはずです。単純パーセプトロンを学ぶことは、人工知能の過去を理解するだけでなく、未来を切り開く鍵となるでしょう。