シグモイド関数:機械学習を支える縁の下の力持ち

AIを知りたい
先生、「シグモイド関数」って難しそうでよくわからないです。もう少し簡単に説明してもらえますか?

AIエンジニア
そうだね、難しく感じるかもしれないね。シグモイド関数は、どんな数字でも0から1の間に変換してくれる関数なんだ。たとえば、黒か白かではなく、灰色も表現できるようにしてくれるようなものだよ。

AIを知りたい
0から1の間の数字に変換するということは、何に役立つんですか?

AIエンジニア
たとえば、コンピュータに猫か猫じゃないかを判断させたいとする。シグモイド関数は、画像が猫である確率を0.8のように表してくれる。0.5より大きければ猫、小さければ猫じゃないと判断できるんだ。
シグモイド関数とは。
人工知能で使われる言葉の一つに「エス字曲線」というものがあります。このエス字曲線は、ロジスティック回帰と呼ばれる予測に使われる関数です。数式で表すと f(x)=11+e-ax(a>0) となり、どんな数字でも0から1の間に変換することができます。例えば、基準値を0.5に設定すると、0.5以上であれば「該当」、0.5未満であれば「該当せず」と判断することで、データを二つの種類に分けることができます。
なめらかな曲線:シグモイド関数の特徴

なめらかな曲線を描くシグモイド関数は、様々な分野で活用されています。その名の通り、S字型の柔らかな曲線を描くこの関数は、入力値がどのような値でも、出力値は常に0から1の間に収まるという、特別な性質を持っています。この性質は、ちょうど材料の種類に関わらず、一定の規格の製品を作り出す機械のようです。
シグモイド関数のこの性質は、確率や割合といった、0から1の範囲で表される事柄を扱う際に特に役立ちます。例えば、ある事柄が起こる可能性を予測する数式を作る場面を考えてみましょう。シグモイド関数を用いることで、予測値は必ず0から1の範囲に収まります。これは、予測値をそのまま可能性として捉えることができるということを意味し、結果の解釈を容易にします。
また、シグモイド関数は、その滑らかな変化も重要な特徴です。入力値が少し変化したときでも、出力値は急激に変化することなく、緩やかに変化します。この滑らかな変化は、数式における安定性を高める役割を果たします。つまり、入力値に多少の誤差があったとしても、出力値への影響は少なく抑えられます。
このように、シグモイド関数は、どんな入力値でも0から1の範囲に変換する能力と、滑らかな変化という二つの大きな特徴を持っています。これらの特徴こそが、シグモイド関数が幅広い分野で応用されている理由であり、様々な場面で役立つ道具となっています。確率の予測だけでなく、人工知能の学習過程における活性化関数など、シグモイド関数の活躍の場は多岐に渡ります。今後も、様々な分野でシグモイド関数の更なる活用が期待されます。
| 特徴 | 説明 | 利点 | 応用例 |
|---|---|---|---|
| 出力範囲 | 0から1の間 | 確率や割合を扱う際に便利 | 確率予測 |
| 曲線形状 | なめらかなS字曲線 | 入力値の変化に対して出力値が緩やかに変化し、安定性が高い | AIの活性化関数 |
予測モデルの要:ロジスティック回帰における役割

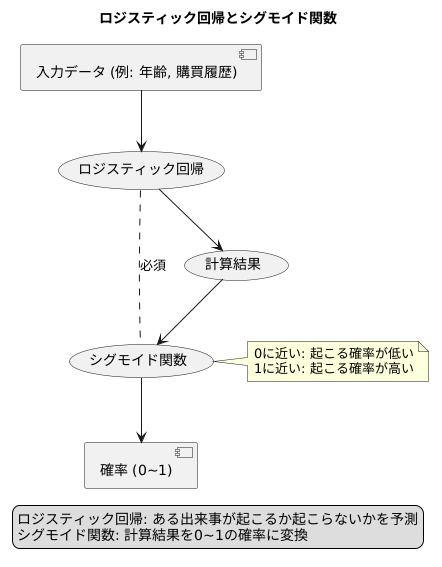
予測する場面でよく使われる手法の一つに、ロジスティック回帰というものがあります。これは、ある出来事が起こるか起こらないかを予測する、二者択一の問題を解くための統計的な方法です。たとえば、お客さんが商品を買うか買わないか、病気になるかならないか、といった問題を扱うことができます。
このロジスティック回帰という手法の中心には、シグモイド関数と呼ばれるものがあります。シグモイド関数は、計算の結果得られた数値を、0から1の間の値に変換する働きをします。この0から1の間の値は、確率として解釈することができます。つまり、0に近いほど起こる確率が低く、1に近いほど起こる確率が高いと判断できます。
たとえば、お客さんが商品を買う確率を予測したいとします。ロジスティック回帰を用いると、お客さんの年齢や過去の購買履歴といった情報をもとに、そのお客さんが商品を買う確率を計算することができます。この計算結果をシグモイド関数に通すことで、0から1の間の値に変換し、確率として表現することができるのです。
シグモイド関数がロジスティック回帰において重要なのは、計算結果を確率というわかりやすい形に変換してくれるからです。もしシグモイド関数がなければ、計算結果はそのままでは確率として解釈することが難しく、予測の精度も落ちてしまいます。
このように、ロジスティック回帰はシグモイド関数と組み合わされることで、様々な予測問題を解くことができる強力な手法となっています。まるで車がエンジンなしでは走れないように、ロジスティック回帰はシグモイド関数なしでは成り立ちません。シグモイド関数は、ロジスティック回帰という車のエンジンにあたる、なくてはならない重要な部品なのです。
二分割問題への応用:閾値による分類

物事を二つに分ける作業は、様々な場面で見られます。例えば、試験の合否判定、商品の不良品検査、メールのスパム判定などです。このような、対象を二つのグループに分類する問題を、二分割問題と呼びます。そして、この二分割問題を解く際に、シグモイド関数というものが役立ちます。シグモイド関数は、滑らかな曲線を描く関数で、その出力値は常に0と1の間に収まります。この0から1の間の値を、ある基準値で区切ることで、二つのグループに分類することが可能になります。
この基準値のことを、閾値(しきいち)と呼びます。例えば、閾値を0.5に設定したとしましょう。シグモイド関数の出力値が0.5以上であれば、その対象はグループAに分類され、0.5未満であればグループBに分類されます。具体的な例を考えてみましょう。ある病気の検査で、シグモイド関数を用いて、陽性か陰性かを判定するとします。検査の結果、シグモイド関数の出力値が0.7だった場合、閾値0.5を上回っているので、陽性と判定されます。逆に、出力値が0.3だった場合は、閾値0.5を下回るので、陰性と判定されます。
この閾値は、状況に応じて調整することができます。例えば、病気の検査では、陰性と判定されるべき人を陽性と判定してしまうと、大きな問題につながる可能性があります。このような場合、誤判定のリスクを減らすために、閾値を0.7や0.8など、より高い値に設定することがあります。逆に、陽性と判定されるべき人を陰性と判定してしまうリスクの方が高い場合は、閾値を0.3や0.2など、より低い値に設定することもあります。このように、閾値を調整することで、状況に応じた最適な分類を行うことができるのです。シグモイド関数と閾値の組み合わせは、まるで、大きさの異なる砂利をふるい分けて選別するように、データを効率よく分類するための、大変便利な道具と言えるでしょう。
| 二分割問題 | 対象を二つのグループに分類する問題。例:試験の合否、商品の不良品検査、メールのスパム判定 |
|---|---|
| シグモイド関数 | 0と1の間の値を出力する滑らかな曲線を描く関数。二分割問題を解くのに役立つ。 |
| 閾値(しきいち) | シグモイド関数の出力値を区切る基準値。 |
| 閾値の例 | 0.5に設定した場合、出力値が0.5以上はグループA、0.5未満はグループBに分類。 |
| 病気検査の例 | 出力値0.7 → 閾値0.5以上 → 陽性 出力値0.3 → 閾値0.5未満 → 陰性 |
| 閾値の調整 | 状況に応じて調整可能。 誤判定リスクを減らすため、高めに設定(例:0.7, 0.8) 陽性を見逃すリスクを減らすため、低めに設定(例:0.3, 0.2) |
計算の簡便さ:微分の容易さ

なめらかな曲線を描くS字型の関数、シグモイド関数には、その変化の割合、つまり微分を計算するのがとても簡単なという、大きな利点があります。この簡便さは一体なぜ重要なのでしょうか。それは、機械学習において、まるで職人が道具を研ぎ澄ますように、学習モデルを少しずつ調整していく過程で、この微分が大きな役割を果たすからです。
機械学習では、集めたデータに基づいて、予測や判断を行う数式を組み立てます。この数式の中に含まれる様々な数値を、ちょうど職人が刃物の角度を細かく調整するように微調整していくことで、より精度の高い予測ができるように学習を進めます。この微調整を行う際に、微分の値が必要となるのです。もし、微分の計算がとても複雑だったら、学習にかかる時間や手間は膨大なものになってしまいます。
シグモイド関数の場合は、その微分を計算するのに、関数自身を使うことができます。つまり、既に計算されているシグモイド関数の値を利用して、簡単に微分を求められるのです。これは、まるで同じ材料を使って別の料理を作るように、効率的で無駄がないと言えます。計算の手間が減るということは、それだけ学習にかかる時間も短縮され、コンピュータの負担も軽減されます。
この微分の容易さこそが、シグモイド関数が機械学習の世界で広く使われてきた理由の一つです。まるで切れ味の良い包丁が料理をスムーズに進めるように、シグモイド関数の微分の容易さは、機械学習の学習過程を効率化し、より良い結果へと導く重要な役割を担っていると言えるでしょう。
| シグモイド関数の利点 | 機械学習における役割 | 具体例 |
|---|---|---|
| 微分の計算が簡単 | 学習モデルの微調整を効率化 | 数式の微調整(刃物の角度調整) |
| 微分にシグモイド関数自身を使用 | 計算の手間と時間を削減、コンピュータの負担軽減 | 同じ材料で別の料理を作る |
| 学習の効率化 | 精度の高い予測の実現 | 切れ味の良い包丁 |
関数の理解:数式とグラフ

関数は、入力と出力の関係を定めた規則のようなものです。ある値を入力すると、それに対応する値が出力されます。この入力と出力の関係を視覚的に分かりやすく示すのがグラフです。
今回取り上げるのは、シグモイド関数と呼ばれる、特別な性質を持った関数です。この関数は、数式で表すと、f(x) = 1 / (1 + exp(-ax)) となります。ここで、xは入力値、f(x)は出力値、そしてaは正の定数です。また、exp(-ax)は、自然対数の底eの-ax乗を表します。
この関数における重要な要素の一つが、定数aです。このaの値を変えることによって、シグモイド曲線の傾き具合を調整できます。aの値が大きければ大きいほど、曲線は急な坂道のような形になり、逆にaの値が小さければ小さいほど、曲線は緩やかな丘のような形になります。
シグモイド関数のグラフを描いてみると、滑らかなS字型の曲線になります。入力値xが負の無限大に近づくにつれて、出力値f(x)は0に近づき、反対に入力値xが正の無限大に近づくにつれて、出力値f(x)は1に近づきます。つまり、出力値は0と1の間の値を滑らかに変化していきます。
このS字型の曲線は、まるで緩やかな坂道を登っていく様子を表しています。最初はゆっくりと登り始め、途中から徐々に傾斜がきつくなり、最後は再び緩やかになって、頂上へと近づいていく様子が目に浮かびます。シグモイド関数は、このような独特の形と性質から、様々な分野で応用されています。
