感度:機械学習における重要指標

AIを知りたい
先生、『Sensitivity』ってAIの分野でよく聞くんですけど、どういう意味ですか?

AIエンジニア
簡単に言うと、『Sensitivity』は、実際に起きた出来事をAIがどれくらい見つけられるかの能力のことだよ。病気の診断で例えると、実際に病気の人を、AIがどれだけ正しく病気だと判断できるかの割合だね。

AIを知りたい
なるほど。実際に病気の人を見つける能力なんですね。じゃあ、値が高いほど良いんですか?

AIエンジニア
その通り!1.0に近いほど、実際に起きた出来事を漏れなく見つけられることを意味する。病気の診断なら、病気の人を見落とす可能性が低いということだね。
Sensitivityとは。
人工知能で使われる「感度」という言葉について説明します。これは統計や機械学習の分野で、結果の再現性の範囲を示す数値です。この値は、理想的には1.0に近づくほど良いとされています。
感度とは

検査や診断の性能を測る大切な指標の一つに、感度というものがあります。これは、実際に何らかの状態、例えば病気にかかっている人の中で、検査によって正しくその状態だと判定された人の割合を示すものです。言い換えれば、ある状態が存在している時に、それを正しく見つける確率のことです。
例として病気の診断を考えてみましょう。ある病気にかかっている人が100人いたとします。その中で、検査を受けた結果、実際に病気だと正しく診断された人が90人だったとしましょう。この場合、感度は0.9となります。感度は0から1までの値を取り、1に近づくほど検査の性能が高いことを示します。つまり、感度が高いほど、本当に状態がある人をより多く、正しく見つけることができるということです。
感度が1に近い、つまり非常に高い検査であっても、全ての人を完璧に見つけることは難しいです。先の例では、病気にかかっている100人のうち、90人は正しく診断されましたが、残りの10人は検査では病気ではないと判定されてしまいました。このように、本当は状態があるのに、検査では見逃されてしまうことを偽陰性と言います。この偽陰性を少なくすることが、病気の早期発見や適切な治療開始に繋がります。
一方で、感度だけに注目してしまうと、別の問題が生じる可能性があります。例えば、非常に感度が高い検査であっても、実際には病気にかかっていない人を誤って病気だと判定してしまう、いわゆる偽陽性が多い可能性も考えられます。そのため、感度に加えて、偽陽性の割合を示す特異度も合わせて考えることが大切です。感度と特異度をバランス良く評価することで、より適切な検査方法を選択することに繋がります。
| 指標 | 説明 | 計算式 | 理想値 | 注意点 |
|---|---|---|---|---|
| 感度 (Sensitivity) | 実際に状態がある人の中で、検査で正しく状態があると判定された人の割合 | 感度 = 真陽性 / (真陽性 + 偽陰性) | 1 | 感度が高いだけでは、偽陽性が多い可能性もあるため、特異度も合わせて考える必要がある |
| 偽陰性 | 実際には状態があるのに、検査では見逃されてしまうこと | – | 0 | 偽陰性を少なくすることで、早期発見や適切な治療開始につながる |
| 偽陽性 | 実際には状態がないのに、検査で状態があると判定されてしまうこと | – | 0 | 偽陽性が多いと、不必要な検査や治療につながる可能性がある |
| 特異度 (Specificity) | 実際に状態がない人の中で、検査で正しく状態がないと判定された人の割合 | 特異度 = 真陰性 / (真陰性 + 偽陽性) | 1 | 感度と合わせて考えることが重要 |
再現率との関係

「感度」とは、機械学習の分野で、検査や診断において、実際に陽性であるものの中から、正しく陽性と判定できた割合のことです。これは、情報検索の分野で用いられる「再現率」と全く同じ考え方です。
再現率は、ある事柄に関係のある資料全体の中で、実際に探し出せた資料の割合を表します。例えば、ある言葉で資料を探すとします。その言葉に関連する資料が全部で100個あり、そのうち80個が検索結果に表示されたとしましょう。この場合、再現率は0.8となります。
感度と再現率はどちらも、本来陽性であるものをどれだけ見逃さずに捉えられるかを示すものです。その計算方法も同じです。そのため、場合によっては感度と再現率が同じ意味で使われることもあります。
機械学習の分野では、作り上げた模型の性能を評価する指標として、感度あるいは再現率を用いるのが一般的です。特に、本当は陽性なのに陰性と判断してしまう間違いをできるだけ少なくしたい場合、感度や再現率は重要な指標となります。
例えば、病気の診断を考えると、病気の人を健康と誤診してしまうのは重大な問題です。このような誤診を見逃さないためには、感度の高い、つまり再現率の高い診断方法が求められます。このように、偽陰性を最小限に抑える必要がある状況では、感度または再現率が重視されるのです。これは、病気の診断に限らず、不正アクセス検知や製品の欠陥検査など、様々な分野で重要となります。
| 指標 | 分野 | 意味 | 計算方法 | 例 |
|---|---|---|---|---|
| 感度 | 機械学習 | 実際に陽性であるものの中から、正しく陽性と判定できた割合 | 陽性と判定されたもの / 実際に陽性であるもの | 病気の診断で、実際に病気の人を正しく病気と診断できた割合 |
| 再現率 | 情報検索 | ある事柄に関係のある資料全体の中で、実際に探し出せた資料の割合 | 検索結果に表示された資料 / 関連する資料全体 | あるキーワードで検索した結果、表示された関連資料 / 全ての関連資料 |
| 共通点 | – | 本来陽性であるものをどれだけ見逃さずに捉えられるかを示す。計算方法も同じ。 | – | – |
感度の計算方法

病気を見つける検査の良し悪しを測る方法の一つに、感度というものがあります。これは、実際に病気にかかっている人の中で、検査によって正しく病気と判定された人の割合を示す指標です。
感度を計算するには、真陽性と偽陰性という二つの値が必要です。真陽性とは、実際に病気の人を、検査でも正しく病気と判定できた数を指します。一方、偽陰性とは、実際には病気であるにもかかわらず、検査では誤って病気ではないと判定された数を指します。
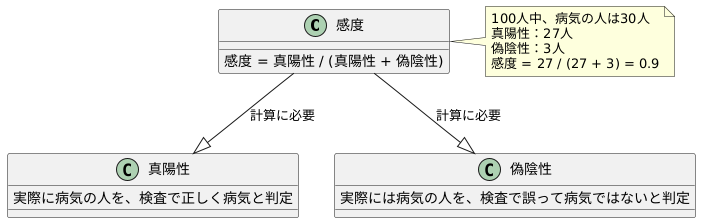
感度は、真陽性の数を、真陽性と偽陰性の数の合計で割ることで計算できます。言い換えると、実際に病気の人全体の中で、どれだけの割合の人が正しく病気と判定されたかを表しています。数式で表すと、感度 = 真陽性 ÷ (真陽性 + 偽陰性) となります。
具体的な例を挙げて考えてみましょう。100人の人に病気の検査をしたとします。その中で、実際に病気の人は30人、病気でない人は70人です。検査の結果、病気の人のうち27人が正しく陽性と判定されました(真陽性)。残りの3人は、病気であるにもかかわらず、陰性と判定されてしまいました(偽陰性)。この場合、感度は 27 ÷ (27 + 3) = 0.9 となります。
この0.9という値は、検査を受けた病気の人全体の90%が正しく病気と診断されたことを意味します。つまり、この検査は実際に病気の人を高い確率で見つけることができる、感度の高い検査と言えるでしょう。ただし、感度が高いだけでは、必ずしも優れた検査とは言えません。病気でない人を誤って病気と判定してしまう偽陽性の割合も合わせて考慮する必要があります。この偽陽性の割合に関連する指標は特異度と呼ばれ、感度と特異度を合わせて検査の性能を総合的に判断することが重要です。
感度の応用例

「感度」とは、本来あるべきものを見つける能力のことを指します。病気の有無を調べる検査を例に挙げると、実際に病気を抱えている人の中で、検査によって正しく陽性と判定された人の割合が感度にあたります。この感度は医療診断以外にも、様々な場面で活用されています。
迷惑メールの振り分けを想像してみてください。受信したメールの山の中から、迷惑メールを正しく迷惑メールだと識別する割合も感度で表されます。迷惑メールを見逃すと、重要な情報を見落としたり、危険な罠にかかったりする可能性があるため、感度の高いフィルターが求められます。
また、クレジットカードの不正利用を見つけるシステムでも感度は重要な役割を担います。不正利用が行われている中で、それを正しく不正利用だと見抜く割合が感度です。不正利用を見逃すと、金銭的な損害だけでなく、個人情報の漏洩といった深刻な事態に繋がる恐れがあります。そのため、高い感度で不正利用を検知できるシステムが不可欠です。
製造の現場でも、製品の欠陥を見つける際に感度が用いられます。不良品が混ざっている中で、それを正しく不良品だと判断する割合が感度です。不良品の出荷は、企業の評判を落とすだけでなく、使用者に危害を与える可能性も孕んでいます。だからこそ、高い感度で欠陥を見つけることが重要になります。
このように、見逃しを許容できない場面では、感度が極めて重要な指標となります。感度を高めることで、目的とする事象を漏れなく捉え、システム全体の信頼性を高めることができます。近年、機械学習の進歩に伴い、感度を基準とした予測模型の評価も重要性を増しています。より正確な予測模型を作るためには、感度を正しく評価し、向上させる必要があります。
| 分野 | 目的 | 感度の意味 | 見逃しのリスク |
|---|---|---|---|
| 医療診断 | 病気の有無を調べる | 実際に病気を抱えている人の中で、検査によって正しく陽性と判定された人の割合 | 病気の発見の遅れ |
| 迷惑メール振り分け | 迷惑メールを識別する | 受信したメールの山の中から、迷惑メールを正しく迷惑メールだと識別する割合 | 重要な情報の見落とし、危険な罠 |
| クレジットカード不正利用検知 | 不正利用を見つける | 不正利用が行われている中で、それを正しく不正利用だと見抜く割合 | 金銭的損害、個人情報漏洩 |
| 製造業 | 製品の欠陥を見つける | 不良品が混ざっている中で、それを正しく不良品だと判断する割合 | 企業の評判失墜、使用者への危害 |
感度の限界

検査や識別において、感度は重要な役割を果たします。感度とは、実際に陽性であるものの中で、正しく陽性と判定されたものの割合を示す尺度です。例えば、病気の検査で考えると、感度は、実際に病気を患っている人の中で、検査によって正しく病気と診断された人の割合を表します。感度が高いほど、真の陽性を多く捉えることができます。これは一見良いことのように思えますが、感度だけに注目すると、落とし穴があります。
感度が高いということは、それだけ多くの陽性を検出しようとする設定になっているということです。この設定は、本来陰性であるものまで陽性と判定してしまう可能性を高めます。これを偽陽性といいます。病気の検査で例えると、健康な人が誤って病気と診断されてしまう状況です。偽陽性が増えると、不必要な治療や検査、そして精神的な負担を強いる可能性があります。
そのため、感度だけを指標として判断するのは危険です。感度と合わせて特異度も考慮する必要があります。特異度は、実際に陰性であるものの中で、正しく陰性と判定されたものの割合を示します。病気の検査では、健康な人が正しく健康と診断される割合です。感度が高いと偽陽性が増えやすく、特異度が高いと偽陰性が増えやすい傾向があります。つまり、感度と特異度はトレードオフの関係にあります。
理想的なモデルは、感度と特異度が共に高い状態です。しかし、現実的には両方を同時に最大化することは難しいです。そこで、目的に合わせて感度と特異度のバランスを調整することが重要になります。例えば、命に関わる病気の検査では、偽陰性で病気を見逃すリスクを減らすために感度を高く設定することがあります。一方、治療のリスクが高い病気の場合は、特異度を高く設定して偽陽性を抑えることが重要になります。このように、状況に応じて適切なバランスを見つけることが、信頼性の高い判断につながります。
| 指標 | 定義 | 例(病気の検査) | 影響 |
|---|---|---|---|
| 感度 | 実際に陽性であるものの中で、正しく陽性と判定されたものの割合 | 実際に病気を患っている人の中で、検査によって正しく病気と診断された人の割合 | 高いと偽陽性が増加、低いと偽陰性が増加 |
| 特異度 | 実際に陰性であるものの中で、正しく陰性と判定されたものの割合 | 健康な人が正しく健康と診断される割合 | 高いと偽陰性が増加、低いと偽陽性が増加 |
他の指標との組み合わせ

適切な予測模型を選ぶには、ただ一つの数値だけで判断するのではなく、様々な角度から見ることが大切です。感度という数値は、本当に陽性であるものの中から、どれほど正確に陽性と予測できたかを示すものですが、これだけでは模型の良し悪しを完全には判断できません。感度に加えて、他の指標も一緒に見ていくことで、より多角的に模型の性能を評価することができます。
例えば、ROC曲線とAUCという指標があります。ROC曲線は、様々な判定の基準で感度と特異度がどのように変化するかを曲線で表したものです。特異度とは、本当に陰性であるものの中から、どれほど正確に陰性と予測できたかを示す数値です。この曲線の下側の面積をAUCと言います。AUCの値が1に近いほど、模型の性能が良いと考えられます。ROC曲線とAUCを見ることで、感度と特異度のバランス、そして模型全体の性能を視覚的に把握することができます。
また、F値という指標も有用です。F値は、感度と適合率の調和平均です。適合率とは、陽性と予測したデータのうち、実際に陽性であったデータの割合を表します。感度は真の陽性を捉える能力、適合率は誤った陽性予測を避ける能力を表すため、F値はこれら両方のバランスを評価します。もし感度だけが極端に高く、適合率が低い場合や、その逆の場合、F値は低くなります。つまり、F値が高いほど、真の陽性を見つける能力と、偽陽性を避ける能力の両方が高いことを示します。
このように、感度だけでなくROC曲線とAUC、F値といった他の指標と組み合わせて使うことで、模型の特性をより深く理解し、目的に最適な模型を選ぶことができます。様々な指標を組み合わせて分析することで、精度の高い予測が可能となり、より良い意思決定に役立ちます。
| 指標 | 説明 | 利点 |
|---|---|---|
| 感度 | 真陽性のうち、正しく陽性と予測できた割合 | 陽性を見つける能力を評価 |
| 特異度 | 真陰性のうち、正しく陰性と予測できた割合 | 陰性を見つける能力を評価 |
| ROC曲線とAUC | 様々な判定基準での感度と特異度の変化を曲線で表示(AUCは曲線下の面積) | 感度と特異度のバランス、モデル全体の性能を視覚的に把握 |
| 適合率 | 陽性と予測したデータのうち、実際に陽性であったデータの割合 | 誤った陽性予測を避ける能力を評価 |
| F値 | 感度と適合率の調和平均 | 真陽性を見つける能力と偽陽性を避ける能力のバランスを評価 |
