規模が性能を決める法則:スケーリング則

AIを知りたい
先生、「スケーリング則」ってよく聞くんですけど、難しくてよくわからないんです。簡単に教えてもらえませんか?

AIエンジニア
いいかい?「スケーリング則」を簡単に言うと、人工知能のモデルを大きくすればするほど、性能が良くなるという法則のことだよ。例えば、模型飛行機を大きく作って、より強力なエンジンを積めば、遠くまで飛ぶようになるのと同じイメージだね。

AIを知りたい
なるほど。大きいほど性能が良くなるんですね。でも、限界はないんですか?

AIエンジニア
いい質問だね。もちろん限界はあるよ。人工知能を大きくするには、たくさんの部品やデータ、そして計算するための電力が必要になる。部品やデータを集めるにも、電力を確保するにも限界があるから、いくらでも大きくできるわけではないんだ。だから、より少ない部品やデータ、電力で性能を上げる方法をみんなが考えているんだよ。
スケーリング則とは。
人工知能に関わる言葉である「規模の法則」について説明します。規模の法則とは、人工知能の模型を大きくしていくと、その性能が上がるという関係を表したものです。具体的には、模型を構成する部品の数、学習に使うデータの量、計算に使う資源の量と、模型の誤りの関係を表しています。部品の数、データの量、計算に使う資源の量のそれぞれを対数で表すと、誤りの量と比例関係があることが分かっています。模型の性能を表す指標である損失は、べき乗則に従って減少していきます。この法則によると、人工知能を大きくすればするほど性能が上がるため、より大きな模型を作る試みが進んでいます。しかし、同時に機械の性能やデータの量には限りがあるため、性能を効率よく上げる方法が探られています。(※PF-daysとは、人工知能の計算量を評価するときの単位です。)
スケーリング則とは

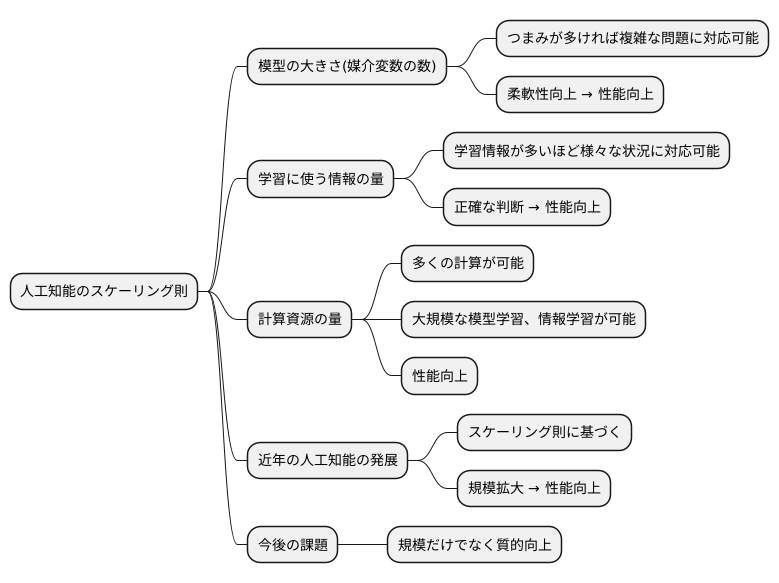
人工知能の世界では、規模が物を言う場面が多くあります。これを明確に示すのが「スケーリング則」です。まるで建物を大きくするほど安定性が増すように、人工知能モデルもその規模を増やすことで性能が向上する傾向を示します。この規模には、三つの主要な要素が関わってきます。
一つ目は「模型の大きさ」です。人工知能モデルは、内部にたくさんの「つまみ」のようなものを持っています。専門的にはこれを「媒介変数」と呼びますが、このつまみを調整することで、様々な問題を解くことができます。つまみの数が多い、つまり模型が大きいほど、複雑な問題に対応できる柔軟性が上がり、結果として性能も向上します。
二つ目は「学習に使う情報の量」です。人間と同じように、人工知能も多くのことを学ぶことで賢くなります。学習に使う情報が多いほど、様々な状況に対応できるようになり、より正確な判断を下せるようになります。
三つ目は「計算資源の量」です。人工知能の学習には、膨大な計算が必要です。高性能な計算機をたくさん使い、多くの計算を行うことで、より大規模な模型を学習させたり、より多くの情報を学習させたりすることが可能になります。これは、性能向上に直結します。
近年の人工知能の急速な発展は、このスケーリング則に基づいた研究開発によるところが大きいです。より多くの媒介変数、より多くの学習情報、そしてより多くの計算資源を投入することで、人工知能はますます賢くなり、私たちの生活を様々な形で変えていくと期待されています。しかし、規模を大きくするだけでは解決できない問題も存在します。今後の研究では、規模だけでなく、質的な向上も目指していく必要があるでしょう。
法則の具体的な関係

物事の規模を大きくすれば、成果も比例して大きくなるとは限りません。例えば、人工知能の学習において、扱う情報量や計算資源を増やすだけでは、必ずしも性能が向上するとは言えないのです。これを説明するのが「スケーリング則」です。この法則は、人工知能の学習において、様々な要素が複雑に絡み合い、性能に影響を与えることを示しています。
具体的には、人工知能のモデルの規模を決める「変数の数」、学習に使う「情報の量」、そして学習に使う「計算能力の大きさ」、これらの3つの要素が、人工知能の性能、特に間違える割合の少なさに関係することが分かっています。しかも、これらの関係は単純な比例関係ではなく、それぞれが対数という特殊な関係で結びついています。
例えば、変数の数を2倍にしても、情報の量を2倍にしても、間違える割合は同じように減りますが、その効果は別々に現れるのです。つまり、変数の数を2倍にする効果と、情報の量を2倍にする効果は、それぞれ異なる側面から性能の向上に貢献します。変数の数を増やすことは、モデルがより複雑な事柄を理解する能力を高めることに繋がります。一方、情報の量を増やすことは、モデルがより多くの例から学習し、一般的な規則をより正確に把握することに繋がります。
このように、スケーリング則は、人工知能の性能向上における各要素の役割を明らかにします。この法則を理解することで、限られた資源の中で、人工知能の設計や学習方法を最適化し、最大限の効果を引き出すことができるようになります。つまり、闇闇に規模を大きくするのではなく、それぞれの要素の効果を理解した上で、資源を適切に配分することが重要なのです。
性能向上の仕組み

計算を行う機械の働きをよくするには、その間違いを減らすことが大切です。この間違いを「損失」と呼びます。損失とは、機械の予想と本当の値との違いのことです。損失が小さければ小さいほど、機械の正答率は高くなります。
機械の性能を上げるには、機械の規模を大きくすることが有効です。規模を大きくするとは、機械の部品を増やすようなものです。部品が増えれば、機械はより複雑な計算ができるようになります。この規模の拡大と損失の減少の関係は、ある法則に従っています。それは、規模を大きくすればするほど、損失は規則的に減っていくという法則です。これを「べき乗則」といいます。
なぜ規模を大きくすると損失が減るのでしょうか?それは、規模が大きい機械は、複雑な模様を見つけ出すのが得意だからです。たくさんの部品を持つ機械は、たくさんの情報を取り込むことができます。そして、多くの情報から多くのことを学ぶことができます。まるで、たくさんの経験を積んだ熟練者のように、機械はより正確な判断ができるようになるのです。
このように、機械の学習能力を高めるには、規模を大きくすることが重要です。規模を大きくすることで、損失を減らし、正答率を高めることができます。そして、より正確な予想ができるようになるのです。この仕組みによって、計算を行う機械は日々進化し、私たちの生活をより豊かにしてくれる可能性を秘めているのです。
大規模モデルの開発競争

近頃、人工知能の分野では、大規模モデル開発を巡る激しい競争が繰り広げられています。この競争の火付け役となったのは、規模を大きくすることで性能が向上するという、スケーリング則の発見です。この法則に基づき、世界中の研究機関や企業が、より多くの部品(パラメータ)、より多くの学習資料(データセット)、そしてより強力な計算能力を投入することで、かつてないほど高性能なモデルを次々と生み出しています。
この傾向は、様々な分野で顕著に見られます。例えば、人間が話す言葉を理解し、文章を生成する自然言語処理の分野では、大規模モデルによって、より自然で滑らかな文章が作られるようになりました。また、写真や動画に写っているものを認識する画像認識の分野では、大規模モデルによって、より正確な認識が可能になっています。さらに、人間の声を認識し、文字に変換する音声認識の分野でも、大規模モデルは、騒音の中でも正確に音声を認識できるようになりました。このように、大規模モデルは人工知能技術の進歩を大きく加速させているのです。
しかし、大規模モデルの開発には、莫大な費用と長い時間が必要となります。高性能な計算機を長時間稼働させる必要があるため、電力消費も膨大になり、環境への負荷も懸念されています。また、大規模な学習資料を集めるにも多大な労力がかかります。そのため、限られた資源で効率的に開発を進めるための方法が、世界中で熱心に研究されています。例えば、学習方法の工夫や、不要な部品を削減する技術などが注目を集めており、これらの技術革新が今後の大規模モデル開発競争の鍵を握ると考えられています。
| 分野 | 大規模モデルの効果 | 課題 |
|---|---|---|
| 自然言語処理 | より自然で滑らかな文章生成 | 莫大な費用と時間、膨大な電力消費、環境負荷、大規模な学習資料収集の労力 |
| 画像認識 | より正確な認識 | |
| 音声認識 | 騒音の中でも正確な音声認識 |
| 現状 | 課題への対策 |
|---|---|
| 大規模モデル開発競争 | 学習方法の工夫、不要な部品削減技術の研究 |
計算資源の限界と新たな挑戦

近年の技術革新は目覚ましく、特に情報処理の分野では様々な計算模型が提案され、目覚ましい成果をあげています。そうした模型の多くは、規模を大きくすれば性能が向上するという共通の性質を持っています。しかし、この考え方をそのまま適用するには、乗り越えなければならない壁が存在します。それは計算資源の限界です。
計算模型を大きくすると、それに伴い必要な計算の量は飛躍的に増大します。高性能の計算機を用いたとしても、無限に規模を拡大し続けることは現実的に不可能です。限られた資源の中で、いかに性能を引き出すかが、これからの技術発展を左右する大きな課題と言えるでしょう。
この課題を解決するために、様々な取り組みが始まっています。まず、計算模型の構造そのものを工夫する試みです。模型の設計をより洗練されたものにすることで、無駄な計算を省き、必要な計算の量を減らすことができます。同時に、計算手順を改善する研究も重要です。より効率的な手順を用いることで、同じ計算量でより多くの成果を得ることが可能になります。
これらの研究の進展を測る指標として、「ペタフロップス・日」という単位が用いられ始めています。「ペタフロップス」とは、一秒間に膨大な回数の計算ができることを示す単位で、「ペタフロップス・日」はその計算能力を一日中使い続けた場合の計算量を表します。この単位を用いることで、様々な計算模型の計算コストを比較検討することができ、限られた資源の中で最も効率的な模型を選択することが可能になります。この指標は、今後の計算資源の有効活用を考える上で、重要な役割を担っていくと考えられます。
| 課題 | 解決策 | 評価指標 |
|---|---|---|
| 計算資源の限界:計算模型の規模拡大に伴う計算量の増大 |
|
ペタフロップス・日:様々な計算模型の計算コストを比較検討 |
