鞍点:機械学習における落とし穴

AIを知りたい
先生、「鞍点」って、なんだか馬の鞍みたいだってイメージは湧くんですけど、AIの学習で問題になるってどういうことですか?

AIエンジニア
いいところに気がつきましたね。まさに馬の鞍のように、ある方向から見ると谷底、別の方向から見ると山頂になっている点のことです。AIの学習では、谷底のように一番低いところが最適な状態なのですが、鞍点に引っかかると、そこが谷底に見えてしまうんです。

AIを知りたい
でも、本当の谷底じゃないのに、どうして谷底に見えてしまうんですか?

AIエンジニア
AIの学習は、坂道を下るように進んでいくのですが、鞍点はどの方向にも平らになっているため、まるで谷底に着いたように学習が止まってしまうのです。だから、本当の谷底、つまり最適な状態にたどり着けないまま学習が終わってしまうことがあるのです。
鞍点とは。
人工知能の分野でよく出てくる言葉に『鞍点』というものがあります。これは、ある方向から見ると一番低い谷底のように見えるのに、別の方向から見ると山の頂上のように見える、ちょっと変わった点のことです。機械学習では、学習を進めるための道筋を決める手がかりとして、誤差と呼ばれる値の大きさを利用します。この誤差を少なくしていくことで、より精度の高い学習結果が得られるのですが、この誤差を表す図に鞍点があると問題が生じます。本来は一番低いところを目指して進んでいく必要があるのですが、鞍点では、ある方向から見ると低いように見えるため、そこで進んで行くのが止まってしまうのです。実際にはまだ一番低いところには辿り着いていないにもかかわらず、進むべき方向が分からなくなってしまうため、学習が止まってしまうという問題が起こるのです。
鞍点とは

鞍点とは、幾つもの広がりを持つ空間における、関数のとある点での特徴を表す言葉です。ある方向から見ると谷底のように最も低い点に見え、別の方向から見ると山の頂上のように最も高い点に見える、そんな不思議な点のことを指します。ちょうど、馬の鞍のような形を思い浮かべると分かりやすいでしょう。
山の頂上は、どの向きに下っても必ず値が小さくなります。これは極大点と呼ばれる点です。逆に、谷底はどの向きに上っても値が大きくなり、極小点と呼ばれます。しかし、鞍点はこれらとは大きく異なります。鞍点は、ある方向には値が小さくなり、別の方向には値が大きくなるという性質を持っています。そのため、全体の形としては、単純な山の頂上や谷底とは異なり、もっと複雑な起伏を持った形になります。
この鞍点という複雑な形の点が、機械学習では時として問題を引き起こすことがあります。機械学習では、関数の値が最も小さくなる点、つまり最適な解を見つけ出すことが目標となります。しかし、学習の過程で鞍点に捕まってしまうと、そこが谷底(極小点)ではないにもかかわらず、それ以上低い場所が見つからず、最適な解に辿り着けないということが起こるのです。まるで、広い土地の中で小さな谷底に迷い込んでしまい、周りを見ても山ばかりで、本当の谷底への道が分からなくなってしまうようなものです。そのため、鞍点をいかに避けるか、あるいは鞍点から脱出する方法は、機械学習における重要な課題の一つとなっています。
| 用語 | 説明 | 機械学習における問題点 |
|---|---|---|
| 鞍点 | ある方向から見ると谷底、別の方向から見ると山の頂上に見える点。馬の鞍のような形。 | 最適な解(極小点)ではないにも関わらず、学習過程で鞍点に捕まると、それ以上低い場所が見つからず、最適解に辿り着けない。 |
| 極大点 | 山の頂上。どの向きに下っても値が小さくなる点。 | – |
| 極小点 | 谷底。どの向きに上っても値が大きくなる点。機械学習では最適解となる。 | – |
機械学習における問題点

機械学習、とりわけ深層学習という手法においては、作り上げた模型の働きを高めるために、誤差と呼ばれるずれを極力小さくする作業が欠かせません。このずれを小さくする作業は、一般的に勾配降下法と呼ばれる方法を用いて行われます。
勾配降下法を分かりやすく説明すると、山の斜面を下っていく様子を想像してみてください。山の頂上から麓まで降りるには、常に最も急な斜面を下っていくのが最短ルートです。勾配降下法も同様に、ずれを表す関数の傾きが最も急な方向へ、模型の調整つまみを少しずつ動かしていくことで、ずれが最も小さくなる場所を探し出すのです。
しかし、この方法には落とし穴があります。山の斜面には、頂上や麓以外にも、平坦な場所が存在することがあります。鞍点と呼ばれるこの平坦な場所は、山の頂上のように見えますが、実際には頂上でも麓でもありません。
勾配降下法を用いてずれを小さくしようとすると、この鞍点に到達した時点で、模型の調整つまみを動かすための手がかりとなる傾きがゼロになってしまうのです。傾きがゼロになると、まるで麓に辿り着いたかのように、ずれを小さくする作業がそこで止まってしまいます。
しかし、実際には鞍点は最もずれが小さい場所ではないため、模型の働きは十分に高まりません。結果として、せっかく模型を作っても、思ったような成果を得られない可能性が出てきてしまうのです。これは、まるで宝探しをしている途中で、宝のありかを示す地図が途中で途切れてしまうようなものです。宝はもう少し先にあるにもかかわらず、地図が途切れた場所で諦めてしまうと、宝は見つかりません。機械学習においても、鞍点という落とし穴に阻まれずに、真にずれが最も小さくなる場所を見つけ出すための、より洗練された方法が必要とされています。
鞍点への対処法

機械学習のモデル学習では、最適なパラメータを見つけることが重要です。このパラメータ探索は、広大な土地で最も低い谷底を探すようなものです。しかし、この土地には谷底だけでなく、鞍点と呼ばれる落とし穴が存在します。鞍点は、ある方向から見ると谷底のように見えますが、別の方向から見ると丘になっている場所です。このような場所に迷い込んでしまうと、モデルの学習が進まなくなります。
この鞍点問題に対処するために、様々な工夫が凝らされています。その一つが勢いを加える手法です。これは、過去の進路の情報も利用して、まるでボールが斜面を転がるように勢いをつけ、鞍点を乗り越えようとするものです。過去の勾配の情報を考慮することで、現在の位置だけでなく、移動の軌跡も利用して最適な方向を見つけ出します。
また、確率的に勾配を計算する手法も有効です。全てのデータを使って勾配を計算するのではなく、無作為に選んだデータを使って計算することで、鞍点に留まりにくくします。これは、でこぼこ道を歩くときに、毎回同じ場所に足を取られないように、少しづつ足場を変えるようなイメージです。
さらに、様々な計算方法が開発されており、より効率的に鞍点問題に対処するための研究が進められています。これらの手法はそれぞれ異なるアプローチで鞍点問題を解決しようと試みており、状況に応じて適切な手法を選択することが重要です。最適なパラメータを見つけるための道のりは険しいですが、これらの手法によってより良い学習成果が期待できます。
| 問題点 | 対策 | イメージ |
|---|---|---|
| 鞍点に陥り、モデル学習が進まなくなる | 勢いを加える手法 過去の勾配情報を利用し、ボールが斜面を転がるように勢いをつける |
ボールが斜面を転がる |
| 鞍点に陥り、モデル学習が進まなくなる | 確率的に勾配を計算する手法 無作為に選んだデータで勾配計算を行い、鞍点に留まりにくくする |
でこぼこ道を歩き、足場を少しずつ変える |
高次元空間での課題

近年の機械学習、特に深層学習の発展は目覚ましいものがありますが、その裏には複雑な最適化問題が潜んでいます。深層学習モデルは、画像認識や自然言語処理といった様々なタスクで高い性能を発揮しますが、これらのモデルは膨大な数のパラメータを調整する必要があります。これは、高次元空間での最適化問題を解くことと等しく、いくつかの困難が伴います。
まず、高次元空間には鞍点と呼ばれる特殊な点が多数存在します。鞍点は、ある方向で見ると谷底のように見え、別の方向で見ると山頂のように見える点です。最適化アルゴリズムは、この鞍点に捉えられてしまうと、そこから抜け出すのが難しく、最適な解にたどり着くことができません。まるで迷路に迷い込んだ探検家のように、鞍点という罠に足止めされてしまうのです。
さらに、空間の次元数が増えるにつれて、鞍点の数は指数関数的に増加します。これは、パラメータの数が増えるほど、最適化がより困難になることを意味します。例えるなら、広い平原を探検するよりも、複雑に入り組んだ山岳地帯を探検する方が、迷子になる可能性が高くなるのと同じです。次元数の増加は、最適化の道筋をより複雑にし、最適解への到達を阻みます。
このように、高次元空間における鞍点問題は、深層学習の性能向上を目指す上で、避けては通れない重要な課題です。この問題を解決するために、様々な研究が行われており、より効率的な最適化アルゴリズムの開発や、鞍点の影響を受けにくいモデルの設計などが進められています。これらの研究の進展は、今後の機械学習の発展を大きく左右するでしょう。
| 課題 | 説明 | 例え |
|---|---|---|
| 鞍点問題 | 高次元空間には鞍点と呼ばれる特殊な点が多数存在し、最適化アルゴリズムが鞍点に捉えられると最適な解にたどり着けない。 | 迷路に迷い込んだ探検家が罠に足止めされる |
| 次元数の増加 | 空間の次元数が増えるにつれて、鞍点の数は指数関数的に増加し、最適化が困難になる。 | 複雑に入り組んだ山岳地帯で迷子になる |
今後の展望

機械学習、とりわけ深層学習は、近年目覚ましい発展を遂げてきました。しかし、その学習過程においては、鞍点問題という困難が立ちはだかります。鞍点とは、ある方向から見ると頂点のように、別の方向から見ると谷底のように見える地点のことです。学習アルゴリズムが鞍点に捕らわれてしまうと、そこから抜け出せず、学習が停滞してしまうことがあります。
この問題を解決するために、より効果的な最適化手法の開発が盛んに行われています。勾配降下法などの従来の手法に加え、鞍点を素早く検知し、適切な方向へ学習を進める新たなアルゴリズムの研究が活発に進められています。例えば、鞍点付近での勾配の振る舞いを解析することで、鞍点であるかどうかを判断し、鞍点から脱出する手法などが提案されています。
また、誤差関数の形状自体を改良する試みも注目を集めています。誤差関数は、機械学習モデルの性能を測る指標であり、学習アルゴリズムはこの関数の値を最小化することを目指します。もし、誤差関数の形状が複雑で鞍点が多く存在する場合、学習は困難になります。そこで、鞍点がそもそも生じにくいような、より滑らかな形状の誤差関数を設計する研究が進められています。
これらの研究の進展は、機械学習モデルの性能向上に直結します。より精度の高い予測、より効率的な学習が可能となり、画像認識、音声認識、自然言語処理など、様々な分野への応用が期待されます。今後、ますます複雑で大規模な機械学習モデルが登場するにつれて、鞍点問題への理解と対策は、機械学習の発展にとって不可欠なものとなるでしょう。
| 問題点 | 解決策 | 効果 |
|---|---|---|
| 深層学習における鞍点問題:学習アルゴリズムが鞍点に捕らわれ、学習が停滞する。 | 1. より効果的な最適化手法の開発 ・鞍点を素早く検知し適切な方向へ学習を進めるアルゴリズム ・例:鞍点付近での勾配の振る舞いを解析 2. 誤差関数の形状の改良 ・鞍点がそもそも生じにくい滑らかな形状の誤差関数を設計 |
・機械学習モデルの性能向上 ・より精度の高い予測 ・より効率的な学習 ・画像認識、音声認識、自然言語処理など様々な分野への応用 |
まとめ

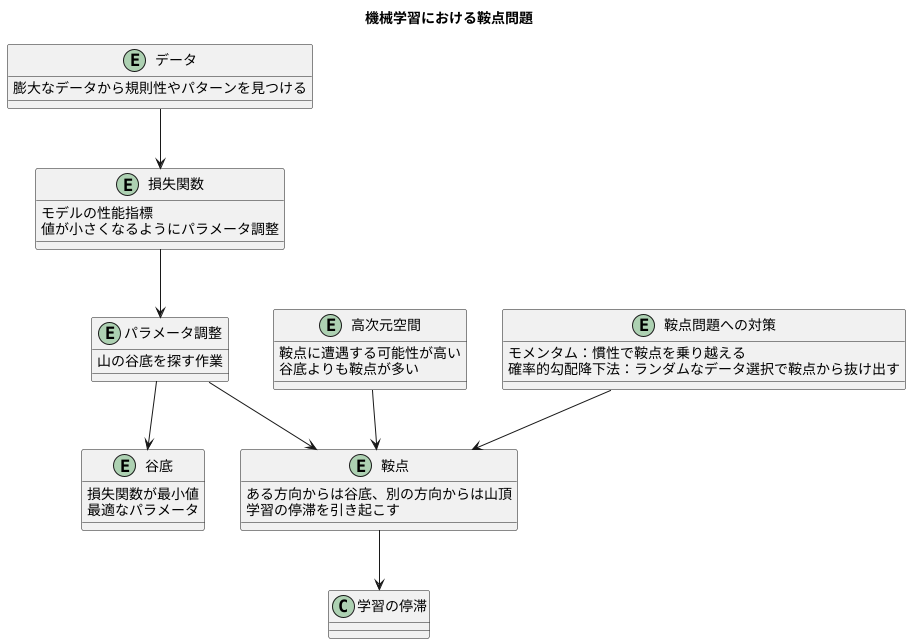
機械学習の目的は、膨大なデータから規則性やパターンを見つけることです。この過程で、モデルの性能を測るための指標となる関数を用います。この関数を損失関数と呼び、この損失関数の値ができるだけ小さくなるようにモデルのパラメータを調整します。この調整作業は、山の谷底を探す作業に例えることができます。谷底は損失関数が最小値となる点であり、最適なパラメータを表します。
しかし、山には谷底だけでなく、鞍点と呼ばれる特殊な場所も存在します。鞍点は、ある方向から見ると谷底のように見えますが、別の方向から見ると山の頂上のように見えます。馬の鞍のような形をしていることから、鞍点と呼ばれます。機械学習の最適化において、この鞍点は大きな問題となります。もし、パラメータ調整の過程で鞍点に到達してしまうと、あたかも谷底に到達したかのように学習が停滞してしまいます。実際には最適なパラメータには到達していないにもかかわらず、それ以上学習が進まなくなってしまうのです。特に、扱うデータの次元数が増えると、鞍点に遭遇する可能性が高くなることが知られています。高次元空間では、谷底よりも鞍点の方が圧倒的に多いため、対策を講じなければ、ほとんどの場合で鞍点に捕まってしまいます。
鞍点問題を回避するための様々な工夫が考えられています。例えば、モメンタムと呼ばれる手法は、パラメータ調整の際に慣性のようなものを加えることで、鞍点を乗り越える力を与えます。まるでボールが坂道を転がり落ちるように、過去の変化の勢いを利用することで、鞍点に捕まらずに谷底を目指せる可能性が高まります。また、確率的勾配降下法も有効な手法の一つです。これは、全てのデータではなく、ランダムに選んだ一部のデータを使ってパラメータを調整する方法です。データの選び方によって変化の向きがランダムに変わるため、鞍点から抜け出せる可能性があります。このように、鞍点問題に対する研究は、機械学習の性能向上に不可欠であり、今後の発展に大きく貢献していくと考えられています。