鞍点:機械学習における課題

AIを知りたい
先生、『鞍点』って難しくてよくわからないのですが、もう少しわかりやすく教えてもらえますか?

AIエンジニア
そうですね。鞍点を理解するのは少し難しいですね。馬の鞍を想像してみてください。鞍の中心は、前後方向から見ると一番低い点ですが、左右方向から見ると一番高い点になっていますよね。鞍点も同じように、ある方向から見ると最小値、別の方向から見ると最大値になっている点のことです。

AIを知りたい
馬の鞍…確かに!なんとなくイメージがわきました。でも、それがAIとどう関係しているのですか?

AIエンジニア
AIの学習では、一番良い結果になるように、誤差を少なくしていく作業を繰り返します。この誤差を少なくしていく過程で、鞍点に引っかかってしまうと、そこが本当に一番誤差が少ない場所ではないのに、それ以上動かなくなって学習が止まってしまうことがあるんです。まるで、谷間に落ち込んでしまったような状態ですね。
鞍点とは。
人工知能の分野でよく使われる「あんてん」という言葉について説明します。あんてんとは、ある方向から見ると一番低い点のように見えて、別の方向から見ると一番高い点のように見える、馬の鞍のような形をした点のことです。機械学習では、誤りの大きさを表す関数にあんてんができてしまうと、実際には一番低い点にたどり着いていないのに、傾きがゼロになってしまうために学習が止まってしまうという問題が起こります。
鞍点とは何か

鞍点とは、いくつもの広がりを持つ空間の中で、ある場所を見た時に、ある方向からは一番低い谷底のように見え、別の方向からは一番高い山頂のように見える、不思議な点のことです。ちょうど馬の鞍のような形をしていることから、鞍点と呼ばれています。
例えば、山脈の中でも、ある方向から見ると山頂に見えても、別の方向から見ると尾根になっている場所があります。鞍点はまさにそのような場所で、平面上ではなく、もっと複雑な空間の中で起こる現象です。
この鞍点という場所は、機械学習の分野で、特になにかを一番良い状態にする問題、つまり最適化問題を扱う際に、しばしば壁となります。 機械学習では、学習の過程で、ある関数の値を最小にする、あるいは最大にするという作業を繰り返します。この作業を最適化と言い、最適化を行うための手法を最適化手法と言います。
最適化手法は、関数の傾きを計算し、その傾きが緩やかになる方向に向かって進んでいくことで、一番低い谷底、あるいは一番高い山頂を探します。しかし、鞍点に差し掛かると、ある方向では傾きが緩やかになっているため、そこが谷底または山頂だと勘違いして、それ以上進まなくなってしまうのです。
実際には、鞍点は谷底でも山頂でもなく、そこからさらに別の進むべき道があるのですが、最適化手法は鞍点の特性上、そこから抜け出すのが難しいのです。そのため、機械学習の最適化において、鞍点への対策は重要な課題となっています。
例えば、鞍点に留まってしまうのを防ぐために、わざと少しだけランダムな動きを加えたり、傾きだけでなく、周りの曲がり具合も考慮に入れたりなど、様々な工夫が凝らされています。
| 用語 | 説明 | 機械学習における問題点 | 対策 |
|---|---|---|---|
| 鞍点 | ある方向からは谷底、別の方向からは山頂のように見える空間上の点。馬の鞍のような形。 | 最適化手法が鞍点で停止し、真の最適解に到達できない。 | ランダムな動きを加える、曲がり具合を考慮するなど。 |
| 最適化 | 関数の値を最小または最大にする作業。 | 鞍点が最適化の妨げになる。 | 鞍点対策が不可欠。 |
| 最適化手法 | 関数の傾きを利用して最適解を探す手法。 | 鞍点で傾きが緩やかになり、停止してしまう。 | 最適化手法の改良が必要。 |
機械学習における問題点

機械学習は、大量の情報を元に、まるで人間のように自ら学び、予測や判断を行う技術です。その学習過程で中心的な役割を果たすのが、誤差関数です。誤差関数は、機械の予測と実際の結果とのズレを数値化したもので、このズレを小さくすることで、機械の予測精度を高めることを目指します。このズレを最小にするために、勾配降下法といった手法がよく使われます。
勾配降下法は、山の斜面を下るように、最も急な方向へ進んでいくことで、谷底、つまり誤差関数の最小値を探し出す方法です。しかし、この方法には落とし穴があります。山の斜面には、谷底のように見えるけれど、実際には谷底ではない場所、鞍点が存在する可能性があるのです。鞍点は、ある方向から見ると谷底のように見えますが、別の方向から見ると山の頂上になっている、馬の鞍のような形をした場所です。
勾配降下法は、斜面の傾きがゼロになる地点で停止します。谷底では傾きがゼロになりますが、鞍点でも傾きがゼロになります。つまり、勾配降下法は、鞍点に到達すると、そこが谷底だと勘違いして停止してしまうのです。これは、まるで登山家が、山頂ではなく、鞍点で登頂成功と勘違いしてしまうようなものです。
結果として、機械学習のモデルは、本来到達できるはずの最適な状態に到達できず、本来発揮できるはずの性能を発揮できなくなってしまいます。この鞍点問題は、機械学習における大きな課題の一つであり、より精度の高い予測を行うためには、この問題を解決するための対策が必要不可欠です。鞍点を回避し、真の谷底を見つけるための様々な研究が行われており、今後の発展が期待されています。
鞍点の視覚化

三次元の空間にある曲面を思い浮かべてみましょう。その表面に、鞍点と呼ばれる特別な点が存在します。この鞍点を理解するために、色々な方向から眺めてみることを想像してみてください。ある方向から見ると、そこはまるで谷底のように深く沈み込んでいるように見えます。まるでボールを置けば、その場所に留まるかのように。しかし、視点を少し変えて別の方向から見ると、今度は山頂のように高く盛り上がって見えます。まるでボールを置けば、転がり落ちてしまうかのようです。
このように、鞍点を中心としたごく小さな範囲でも、眺める方向によって、まるで谷底と山頂が入れ替わるかのような不思議な性質を持っています。ある方向には下向きに傾斜し、別の方向には上向きに傾斜しているのです。この複雑な形状が、鞍点の特徴です。
この三次元的な鞍点の特性を、より分かりやすくするために、二次元の平面に投影して考えてみましょう。すると、馬の鞍のような形が見えてきます。馬の鞍は、人が座る部分が窪んでおり、前後方向には谷のように沈み込んでいます。一方で、左右方向には山のように盛り上がっています。まさに、三次元の鞍点で見た、ある方向には谷、別の方向には山という特徴が、この馬の鞍の形にそのまま表れているのです。この形状が、鞍点の名前の由来となっています。
機械学習の分野では、最適化アルゴリズムを用いて、この曲面上で最も低い谷底を探し求めます。しかし、鞍点のような場所が存在すると、アルゴリズムが騙されてしまうことがあります。アルゴリズムは、鞍点で谷底を見つけたと思ってしまうかもしれません。しかし、実際にはそれは本当の谷底ではなく、別の方向には登り坂が続いているのです。このように、鞍点は最適化アルゴリズムを混乱させる、厄介な存在なのです。
鞍点への対処法

機械学習において、目的関数の最適化は極めて重要です。最適化アルゴリズムは、最も良い設定を見つけるために勾配をたどって関数の谷底を探しますが、鞍点と呼ばれる平坦な領域でつまずくことがあります。鞍点は、ある方向で見れば谷底のように見えますが、別の方向で見れば尾根のように見えるため、学習の停滞を引き起こす厄介な存在です。
この鞍点問題に対処するために、様々な工夫が凝らされています。例えば、勢いをつける方法があります。これは、過去の勾配の情報を考慮することで、まるでボールが坂道を転がるように勢いをつけ、鞍点を乗り越えやすくするものです。勾配が小さくなったからといってすぐに停止するのではなく、過去の勾配の力を借りてさらに進もうとすることで、浅い鞍点ならば難なく突破できます。
また、データの選び方を変える方法も有効です。全てのデータを使って勾配を計算するのではなく、無作為に選んだデータから勾配を計算することで、鞍点にぴったりとはまることを防ぎます。データの選び方が変われば、勾配の方向も変わり、鞍点から脱出する可能性が高まります。これは、でこぼこ道を歩く際に、毎回少し違う場所を踏むことで、一つの穴に足を取られないようにするイメージです。
さらに、より高度な計算方法も開発されています。これらの方法は、勾配だけでなく、関数の曲がり具合なども考慮に入れて、より効率的に最適な値を探し出します。まるで熟練の登山家が、地形を読み解きながら最短ルートで山頂を目指すように、複雑な地形でも迷わず最適な解へとたどり着けるのです。これらの技術革新は、鞍点問題による学習の停滞を克服し、より高性能なモデルの開発に役立っています。
| 問題点 | 対策 | イメージ |
|---|---|---|
| 鞍点での学習の停滞 | 勢いをつける(過去の勾配情報を利用) | ボールが坂道を転がる |
| 鞍点での学習の停滞 | データの選び方を変える(無作為抽出) | でこぼこ道を歩く際に、毎回少し違う場所を踏む |
| 鞍点での学習の停滞 | 高度な計算方法(勾配+関数の曲がり具合) | 熟練の登山家が地形を読み解きながら最短ルートで山頂を目指す |
高次元空間での課題

私たちのよく知る平面や空間といった低い次元の世界では、グラフの谷底のような場所、つまり鞍点を見つけることはあまりありません。しかし次元が増えていくと、不思議なことに、この鞍点が至る所に現れ始めます。ちょうど、高次元空間という広大な土地に、無数の小さな谷が散らばっているような状態です。
機械学習は大量のデータ、すなわちたくさんの特徴量を持つ高次元データを扱うことが多く、この鞍点問題は深刻な壁となります。学習の目的は、この高次元空間の中で最も低い谷底、つまり全体的な最小値を見つけることですが、無数に存在する鞍点に捕まってしまうと、そこから抜け出せなくなってしまうのです。まるで迷路に迷い込んだ旅人のように、アルゴリズムは本当の最適解にたどり着けず、迷子になってしまいます。
さらに厄介なことに、高次元空間には鞍点だけでなく、局所最適解と呼ばれる落とし穴もたくさんあります。これは、全体で見れば最低地点ではないものの、周りの狭い範囲では最低地点のように見える場所です。まるで深い穴の底に小さな窪みがたくさんあるようなもので、アルゴリズムはこれらの窪みに落ち込んでしまうと、なかなか抜け出せず、全体的な最小値を見つけることができません。
このように、高次元空間における最適化は、複雑で難しい問題です。現在も多くの研究者が、より効率的に、そして確実に最適解を見つけ出すための、新しい方法を探求しています。高次元空間の特殊な性質をより深く理解することが、この難問を解く鍵となるでしょう。まるで暗闇の中を手探りで進むように、研究者たちは最適化問題の解決を目指し、日々挑戦を続けています。高次元空間の謎を解き明かすことで、機械学習はさらに進化し、私たちの生活をより豊かにしてくれると期待されています。
| 次元 | 特徴 | 機械学習への影響 |
|---|---|---|
| 低次元 | 鞍点は少ない | 問題が少ない |
| 高次元 | 鞍点と局所最適解が無数に存在 | 最適解にたどり着けない(鞍点)、局所最適解に陥る |
今後の展望

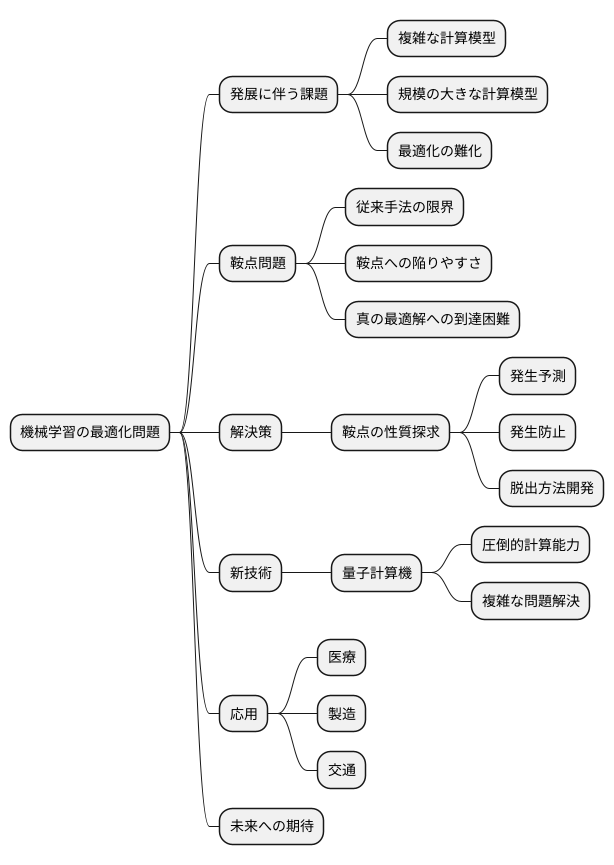
機械学習は目覚ましい発展を遂げ、私たちの暮らしを大きく変えつつあります。より複雑で規模の大きな計算模型を作ることで、これまで以上に高度な課題解決が可能になると期待されています。しかし、この発展に伴い、計算模型を最適な状態に調整する作業、つまり最適化問題はますます難しくなっています。
最適化の過程では、鞍点と呼ばれる落とし穴に陥ることがあります。これは、ある方向から見ると谷底のように見えるものの、別の方向から見ると山頂となっている特殊な点です。従来の調整方法では、この鞍点に捕まってしまい、真の最適解に辿り着けない可能性が高まっています。そのため、より高度な調整方法の開発は喫緊の課題と言えるでしょう。
具体的には、鞍点の性質をより深く探求し、いつ、どこで、なぜ鞍点が現れるのかを予測する必要があります。そして、その発生を未然に防いだり、鞍点から抜け出すための新しい手法の開発が欠かせません。これらの研究が進展することで、計算模型の性能が飛躍的に向上し、医療、製造、交通など、様々な分野で私たちの生活をより豊かにする応用が期待されます。
さらに、量子計算機のような革新的な計算技術も、最適化問題解決に新たな光をもたらす可能性を秘めています。量子計算機の持つ圧倒的な計算能力は、従来の手法では不可能だった複雑な最適化問題の解決を可能にするかもしれません。今後の研究の進展は、機械学習の未来を大きく左右する重要な鍵となるでしょう。私たちは、その進展を見守り、新たな可能性に期待を寄せたいと思います。