予測精度を測る指標:二乗平均平方根誤差

AIを知りたい
先生、「平均二乗パーセント誤差の平方根」って、何ですか?名前が難しくてよく分かりません。

AIエンジニア
そうだね、少し複雑な名前だね。簡単に言うと、これは予測した値が実際の値からどれくらいずれているかをパーセントで表し、そのずれの大きさを測る尺度だよ。たとえば、来月のアイスクリームの売上を予測したとして、その予測が実際の売上と比べてどれくらい近いか遠いかをパーセントで見て、そのずれ具合を平均的に計算したものなんだ。

AIを知りたい
パーセントでずれをみるんですね。でも、なぜ二乗して平方根をとるんですか?

AIエンジニア
良い質問だね。二乗するのは、ずれがプラスでもマイナスでも関係なく、ずれの大きさを測るためだよ。プラスとマイナスが混ざっていると、相殺されてずれの大きさが正しく測れないからね。そして、平方根をとるのは、二乗したことで元の値よりも大きくなったずれの尺度を、元の値と同じスケールに戻すためなんだ。
平均二乗パーセント誤差の平方根とは。
人工知能の分野で使われる「二乗した平均のパーセント誤差の平方根」について説明します。これは、機械学習の分野で、予測の正確さを評価するために使われます。
誤差指標の役割

機械学習の分野では、作った模型の働きぶりを確かめるために、誤差指標を使います。これは、模型が予想した値と実際に起きた値との違いを数値で表したものです。模型の出来不出来を正しく判断するには、目的に合った適切な指標を選ぶことがとても大切です。指標には様々な種類があり、それぞれ異なる観点から模型の性能を評価します。
例えば、単純に誤差の平均を見るだけでなく、誤差のばらつき具合も重要な指標となります。ばらつきが大きいと、模型の予想が不安定で信頼性に欠けると言えます。また、ある特定の状況で誤差が特に大きくなる場合もあります。例えば、病気の診断模型では、病気を見逃す誤差は、病気でない人を病気と診断する誤差よりも重大です。このような場合、誤りの種類によって重み付けをした指標を用いる必要があります。
指標を正しく理解し、目的に合わせて使い分けることで、より精度の高い模型を作ることができます。一つの指標だけで判断するのではなく、複数の指標を組み合わせて多角的に評価することが、本当に目的に合った良い模型を選ぶために必要です。例えば、平均的な誤差が小さくても、特定の状況で大きな誤差が出る模型は、実用上問題となる可能性があります。また、誤差のばらつきが大きい模型も、安定した性能が求められる場面では使いにくいでしょう。このように、様々な指標を組み合わせて総合的に判断することで、より信頼性の高い模型を選択できます。
| 指標の種類 | 説明 | 使用場面 |
|---|---|---|
| 平均誤差 | 誤差の平均値。 | 誤差の全体的な大きさを知りたい場合。 |
| 誤差のばらつき | 誤差のばらつき具合。 | 予測の安定性を評価したい場合。 |
| 重み付け誤差 | 誤りの種類によって重み付けをした指標。 | 誤りの種類によって重大さが異なる場合。 |
二乗平均平方根誤差とは

二乗平均平方根誤差(によく使われる略称は「にじょうへいきんへいほうこんごさ」で、英語のRoot Mean Squared Percentage Errorの頭文字をとってRMSPEとも呼ばれます)は、予測した値と実際に測った値の差がどれくらいかをパーセントで示す指標です。この指標を使うと、異なる単位や規模を持つデータでも比べやすくなります。例えば、会社の売上高と株価のように、全く異なる種類のデータを比較する場合に役立ちます。
二乗平均平方根誤差を計算するには、まずそれぞれのデータについて、予測値と実測値の差を実測値で割ってパーセント誤差を求めます。次に、それぞれのパーセント誤差を二乗します。二乗することで、大きな誤差はより大きな値となり、小さな誤差はより小さな値となります。これは、予測が大きく外れた場合の影響をより重視することを意味します。例えば、パーセント誤差が10%の場合、二乗すると100になり、パーセント誤差が1%の場合、二乗すると1にしかなりません。
次に、二乗したパーセント誤差をすべて足し合わせ、データの数で割って平均値を求めます。最後に、その平均値の平方根を計算することで、二乗平均平方根誤差が得られます。平方根を計算することで、二乗によって大きくなった値を元のスケールに戻し、解釈しやすくします。
二乗平均平方根誤差は、外れ値、つまり予測値と実測値の差が極端に大きいデータの影響を受けやすいという特徴があります。これは、二乗によって大きな誤差が強調されるためです。そのため、外れ値が多いデータに適用する場合には注意が必要です。しかし、逆に言えば、大きな誤差を特に問題視する場合には、この指標が有効に働きます。例えば、機械の故障予測など、大きな誤差が重大な結果につながるケースでは、二乗平均平方根誤差を用いることで、より慎重な予測モデルを構築することができます。
| 用語 | 説明 | 計算方法 | 特徴 |
|---|---|---|---|
| 二乗平均平方根誤差 (RMSPE) |
予測値と実測値の差をパーセントで示す指標。異なる単位や規模のデータ比較が可能。 | 1. 各データの予測値と実測値の差を実測値で割り、パーセント誤差を求める。 2. 各パーセント誤差を二乗する。 3. 二乗したパーセント誤差を合計し、データの数で割る。 4. 平均値の平方根を計算する。 |
外れ値の影響を受けやすい。 大きな誤差を重視する場合に有効。 |
計算方法と解釈

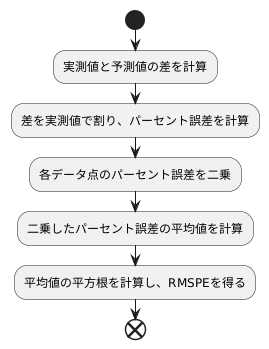
二乗平均平方根誤差(RMSPE)は、予測の精度を評価するための指標で、実測値に対する予測値のずれの大きさを割合で示します。この指標を算出するには、いくつかの段階を踏みます。まず、それぞれのデータについて、実測値と予測値の差を求めます。これは、予測がどれだけ実測値から外れているかを示す値です。次に、この差を実測値で割ることで、それぞれのデータ点における誤差の割合を計算します。この割合をパーセントで表すと、パーセント誤差となります。
次に、それぞれのデータ点のパーセント誤差を二乗します。これは、大きな誤差の影響をより強く反映させるためです。二乗することで、正負の値も正の値となり、すべての誤差を正の値で評価できます。そして、これらの二乗したパーセント誤差の平均値を計算します。これは、全体的な誤差の大きさを示す値です。
最後に、この平均値の平方根を計算することで、RMSPEが得られます。平方根を計算することで、元のパーセント誤差と同じ尺度に戻し、解釈しやすくします。RMSPEの値は、予測値が実測値から平均的にどれくらいずれているかを割合で示しています。例えば、RMSPEが10%の場合、予測値は平均的に実測値から10%ずれていると解釈できます。RMSPEの値が小さいほど、予測の精度は高いと言えます。つまり、実測値と予測値のずれが小さいことを示します。
ただし、RMSPEを用いる際には注意が必要です。実測値がゼロに近い値の場合、パーセント誤差の計算が不安定になる可能性があります。これは、ゼロで割ることができないためです。このような場合、RMSPEの値が非常に大きくなり、予測の精度を正しく評価できない場合があります。そのため、実測値にゼロに近い値が含まれる場合は、RMSPEだけでなく、他の指標も合わせて用いることで、予測の精度をより多角的に評価することが重要です。
他の指標との比較

予測の正確さを確かめるには、いくつかの方法があります。それぞれに特徴があるので、どれを使うかは、何を明らかにしたいかによって変わってきます。よく使われる指標の一つに、平均絶対パーセント誤差というものがあります。これは、実際の値と予測値の差を、実際の値で割って百分率で表したものです。この指標は、どのくらいずれているかを相対的に示すので、異なる規模のデータを比べる際に便利です。
しかし、この指標は、実際の値がゼロに近い場合、計算が不安定になることがあります。そこで、二乗平均平方根パーセント誤差という指標が用いられます。これは、各データの実際の値と予測値の差を二乗し、平均を取り、平方根を求めた後、実際の値で割って百分率で表したものです。二乗することにより、大きなずれにより大きなペナルティを与えるため、より正確さを追求する場合に適しています。
一方、平均二乗誤差という指標もあります。これは、実際の値と予測値の差を二乗し、その平均を求めたものです。この指標は、絶対的なずれを表すため、データの規模が同じ場合に有効です。しかし、データの規模が異なると、比較が難しくなります。
これらの指標は、それぞれ異なる視点から予測の正確さを評価します。単一の指標だけで判断するのではなく、複数の指標を組み合わせて総合的に評価することで、より信頼性の高い結果を得ることができます。例えば、二乗平均平方根パーセント誤差で全体的なずれを確認し、平均二乗誤差で特定のデータのずれを詳しく調べるといった使い分けが有効です。このように、目的に合わせて指標を使い分けることで、より精度の高い予測モデルを作ることができます。
| 指標名 | 計算方法 | 特徴 | 長所 | 短所 |
|---|---|---|---|---|
| 平均絶対パーセント誤差 | ( | 実際の値 – 予測値 | ) / 実際の値 * 100% | 相対的なずれ | 異なる規模のデータ比較に便利 | 実際の値がゼロに近い場合、不安定 |
| 二乗平均平方根パーセント誤差 | √( ( (実際の値 – 予測値)^2 の平均) ) / 実際の値 * 100% | 大きなずれに大きなペナルティ | 正確さを追求する場合に適している | – |
| 平均二乗誤差 | (実際の値 – 予測値)^2 の平均 | 絶対的なずれ | データの規模が同じ場合に有効 | データの規模が異なると比較が難しい |
適用事例

需要予測、売上予測、株価予測といった、実際の値がゼロより大きい場合に、その相対的な誤差を評価することが大切な場面で、平均平方二乗誤差の平方根(RMSPE)は幅広く役立てられています。
例えば、小売業を見てみましょう。
商品の需要を予測する際にRMSPEを使うことで、どれだけの商品を仕入れるのが最適か、つまり在庫管理を最適化することができます。
需要を正確に予測できれば、売れ残りを減らすだけでなく、機会損失も減らすことができ、結果として売上の向上に繋がります。過剰な在庫は保管コストを増大させ、一方で在庫不足は販売機会を逃すことに繋がるため、正確な需要予測は大変重要です。RMSPEはより精度の高い需要予測を可能にし、無駄なコストの削減と売上の増加に貢献します。
金融業界では、株価予測モデルの評価によくRMSPEが使われます。
株価の変動は、投資における利益と損失に直結するため、その変動率を正確に予測することはリスク管理において非常に重要です。RMSPEを用いることで、株価変動の予測精度を測り、より確実な投資判断を行うことができます。
医療分野でもRMSPEの活用が進んでいます。
患者の状態を予測する際にRMSPEを用いることで、より適切な治療方針を決定することに役立ちます。
例えば、病気の進行度合いを予測することで、適切な投薬量や治療方法を判断し、患者にとって最適な医療を提供することができます。
このように、RMSPEは小売業、金融業、医療分野だけでなく、様々な分野で予測精度を高めるための重要な指標として活用されています。
より精度の高い予測は、企業の経営判断や、人々の生活の質の向上に大きく貢献しています。
| 分野 | RMSPEの活用例 | 効果 |
|---|---|---|
| 小売業 | 商品の需要予測、在庫管理の最適化 | 売れ残り削減、機会損失削減、売上向上 |
| 金融業 | 株価予測モデルの評価、リスク管理 | より確実な投資判断 |
| 医療分野 | 患者の状態予測、治療方針の決定 | 適切な投薬量・治療方法の決定、最適な医療の提供 |
注意点と限界

二乗平均平方根誤差(RMSPE)を用いる際には、いくつかの注意点と限界を理解しておくことが重要です。まず、RMSPEは実際の値がゼロに近い場合、不安定になることがあります。これは、計算式においてゼロで割ることになるためです。もしも、実際の値にゼロが含まれるデータを集めたものを使う場合は、特に注意が必要です。ゼロが含まれると、RMSPEの値が非常に大きくなるか、計算できない場合があります。そのため、そのようなデータにRMSPEを適用する場合は、ゼロに近い値を小さな正の値に置き換える、あるいはRMSPE以外の指標を検討するなどの対策が必要となります。
次に、RMSPEは極端に大きかったり小さかったりする値、つまり外れ値の影響を受けやすい指標です。もしもデータの中に外れ値が含まれていると、RMSPEの値が大きく歪められてしまう可能性があります。例えば、少数の非常に大きな外れ値によって、全体的な誤差が過大評価されることがあります。このような外れ値の影響を少なくするために、あらかじめ外れ値を除外しておく、あるいは外れ値の影響を受けにくい他の指標と合わせて使うといった対策が考えられます。具体的には、中央値を用いる指標や、外れ値を特定の値で置き換えるといった方法があります。
最後に、RMSPEは相対的な誤差を評価する指標であるという点に注意が必要です。つまり、RMSPEは予測値と実際の値の比率を見て、どれくらい予測が外れているかを評価します。しかし、予測値そのものの大きさについては何も示していません。例えば、実際の値が1と100の場合、それぞれに対する予測値が2と200だとすると、どちらの場合もRMSPEは同じ値になります。しかし、明らかに予測のずれの大きさは異なります。そのため、予測値の大きさも評価したい場合は、二乗平均平方根誤差(RMSE)のような、絶対的な誤差を評価する指標と合わせてRMSPEを用いることが重要です。これらの点を踏まえ、データの特性や分析の目的に適切な指標を選択する必要があります。
| 注意点/限界 | 説明 | 対策 |
|---|---|---|
| ゼロに近い値への不安定性 | 実際の値がゼロに近い場合、計算が不安定になり、RMSPEが非常に大きくなるか、計算できなくなる。 | ゼロに近い値を小さな正の値に置き換える、RMSPE以外の指標を検討する。 |
| 外れ値の影響を受けやすい | 外れ値によってRMSPEが大きく歪められ、全体的な誤差が過大評価される可能性がある。 | 外れ値を除外する、外れ値の影響を受けにくい指標(中央値を用いる指標など)と合わせて使う、外れ値を特定の値で置き換える。 |
| 相対的な誤差の評価 | 予測値と実際の値の比率で誤差を評価するため、予測値の大きさについては示していない。 | 予測値の大きさも評価したい場合は、RMSEのような絶対的な誤差を評価する指標と合わせて用いる。 |
