RMSLE:機械学習の評価指標

AIを知りたい
先生、「RMSLE」(平均二乗対数誤差)って、どういう意味ですか?よくわからないんです。

AIエンジニア
RMSLEは、予測値と正解値の差を対数で見て、その差の二乗の平均をルートで求めたものだよ。簡単に言うと、予測値と正解値の比率のずれを見る指標だね。

AIを知りたい
比率のずれを見る、ということは、例えば家の価格を予測する場合、実際の価格が1億円の家を1億1000万円と予測するのと、100万円の家を110万円と予測するのは、同じように評価されるってことですか?

AIエンジニア
その通り!どちらも1.1倍のずれなので、RMSLEでは同じような誤差として扱われる。だから、高い値と低い値が混在するようなデータで、比率のずれを重視したい場合にRMSLEは有効なんだ。
RMSLEとは。
機械学習でよく使われる「RMSLE」という用語について説明します。RMSLEは「平均二乗対数誤差」の略です。この誤差は、予測値と正解値の対数の差を二乗したものの平均値の平方根で表されます。ただし、対数の差は「正解値の対数から予測値の対数を引いたもの」でも、「予測値の対数から正解値の対数を引いたもの」でも、どちらでも構いません。
はじめに

機械学習の手法を用いて予測を行う際には、その予測の正確さを確かめることが欠かせません。作った予測の良し悪しを評価することで、手法の選択や改良に役立てられるからです。そのためには、予測の正確さを測るための適切な物差し、つまり評価指標を選ぶことが重要になります。色々な評価指標の中からどれを使うべきかは、扱う問題の種類や目的によって異なります。今回の記事で取り上げる平均二乗対数誤差(RMSLE)は、回帰問題と呼ばれる、連続した数値を予測する問題で使われる指標の一つです。
平均二乗対数誤差は、予測値と実際の値の比率に着目した指標です。例えば、ある製品の売れ行きを予測する問題を考えてみましょう。100個売れると予想して90個だった場合と、10個売れると予想して1個だった場合、どちらも10個の誤差があります。しかし、最初の場合は売れ行きの規模に対して誤差が小さいのに対し、後の場合は誤差が大きいです。平均二乗対数誤差は、このような規模の違いを考慮に入れて、予測の正確さを評価します。そのため、実際の値の大きさが大きく変動するようなデータに適しています。
平均二乗対数誤差の計算方法は、まず予測値と実際の値の対数を取り、その差を二乗します。そして、全てのデータ点について二乗した差の平均を求め、最後にその平方根を計算します。対数を取ることで、大きな値の影響が小さくなり、比率の違いに注目することができます。二乗する理由は、誤差の正負を打ち消し、大きな誤差をより強調するためです。
平均二乗対数誤差は、値が小さいほど予測の正確さが高いことを示します。誤差が全く無い、つまり完璧な予測の場合は、平均二乗対数誤差は0になります。平均二乗対数誤差を使うことで、予測値と実際の値の比率に着目した評価が可能になり、より適切なモデル選択や改良を行うことができます。
| 評価指標 | 種類 | 特徴 | 計算方法 | 適用場面 |
|---|---|---|---|---|
| 平均二乗対数誤差 (RMSLE) | 回帰問題 | 予測値と実際の値の比率に着目。値の大きさが大きく変動するデータに適している。 | 1. 予測値と実際の値の対数を取る 2. 差を二乗する 3. 全てのデータ点の二乗差の平均 4. 平方根を計算 |
実際の値の大きさが大きく変動するデータ (例: 製品売上予測) |
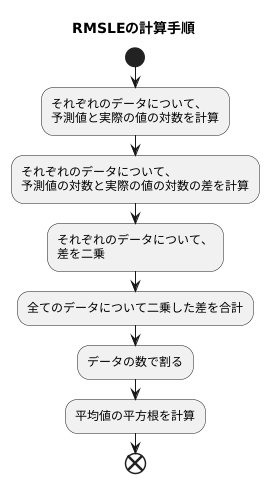
計算方法

二乗平均平方根対数誤差(RMSLE)は、予測値と実際の値の比率に着目した評価指標です。名前の通り、計算は複数の手順で行います。まず、それぞれのデータについて、予測値と実際の値の対数を計算します。対数は、一般的に自然対数と呼ばれる、ネイピア数と呼ばれる特別な数を底とする対数を用います。このネイピア数は、円周率のように数学的に重要な意味を持つ数です。対数を使うことで、大きな値の差を小さく扱い、小さな値の差を大きく扱う効果が得られます。つまり、実際の値が10で予測値が100の場合と、実際の値が1000で予測値が10000の場合を、同じくらいの誤差として扱うことができます。次に、それぞれのデータについて、予測値の対数と実際の値の対数の差を計算し、その差を二乗します。二乗することで、正負の符号をなくし、誤差の大きさを正の値で表すことができます。全てのデータについて二乗した差を合計し、データの数で割ります。これは、二乗した誤差の平均値を求める操作にあたります。最後に、この平均値の平方根を計算します。平方根を計算することで、元の誤差の尺度に戻し、より解釈しやすい値にします。RMSLEは、特に予測値と実際の値の比率が重要な場合に有効な指標です。例えば、商品の売上予測など、実際の値が大きく変動する場合、RMSEなどの指標では大きな値の誤差の影響が大きくなりすぎてしまいます。RMSLEは対数変換を行うことで、比率に着目した評価を可能にし、このような問題を回避できます。全体として、RMSLEは複雑な計算式に見えますが、各手順には明確な意味があり、予測の精度を評価するための強力な道具となります。
通常の誤差との違い

通常の誤差とRMSLE(二乗平均平方根対数誤差)の違いについて説明します。誤差とは、予測値と実際の値のずれのことです。よく使われる誤差指標にRMSE(二乗平均平方根誤差)がありますが、RMSLEはRMSEとは異なる特徴を持っています。RMSEは、予測値と実際の値の差を二乗して平均を求め、その平方根を計算します。このため、大きな値を持つデータの影響を強く受けます。例えば、ある商品の売上の予測で、実際の売上が10個だったのに対し、予測が1個だった場合と、実際の売上が1000個だったのに対し、予測が999個だった場合を比べてみましょう。RMSEでは後者の誤差の方がずっと大きく評価されます。しかし、割合で考えるとどちらも1個の差であり、相対的な誤差は同じくらいです。
一方、RMSLEは、予測値と実際の値の対数をそれぞれ計算し、その差を二乗して平均を求め、平方根を計算します。対数を使うことで、大きな値の影響を軽減することができます。先ほどの例で考えると、RMSLEではどちらの場合もほぼ同じ誤差として評価されます。つまり、RMSLEは、予測値と実際の値の比率に着目していると言えます。10と1を比べた場合と、1000と100を比べた場合、RMSEでは後者の誤差を大きく評価しますが、RMSLEではどちらも10倍の比率として、同じ程度の誤差として評価します。このように、RMSLEは相対的な誤差を重視する場合に適した指標です。特に、データの範囲が広い場合や、小さな値の誤差を重視したい場合に有効です。
| 項目 | RMSE | RMSLE |
|---|---|---|
| 定義 | 予測値と実測値の差の二乗平均の平方根 | 予測値と実測値の対数の差の二乗平均の平方根 |
| 特徴 | 大きな値の影響を強く受ける。絶対誤差を重視 | 大きな値の影響を受けにくい。相対誤差を重視 |
| 例(実測値10, 予測値1) | 誤差大 | 誤差小 |
| 例(実測値1000, 予測値999) | 誤差大 | 誤差小 |
| 比率に着目 | × | ○ |
| 適用ケース | データの範囲が狭い場合 | データの範囲が広い場合、小さな値の誤差を重視したい場合 |
適用事例

二乗平均平方根対数誤差(RMSLE)は、予測値と実際の値の比率に着目した指標であり、予測値と実際の値の規模に大きな差がある場合に特に役立ちます。たとえば、商品の販売数を予測する場面を考えてみましょう。ある商品は数百個売れる一方、別の商品は数万個売れるといったように、販売数には大きなばらつきが生じることがあります。このような場合、従来の二乗平均平方根誤差(RMSE)を用いると、販売数の多い商品の予測誤差が全体の評価に過剰に影響を与えてしまう可能性があります。一方、RMSLEを用いることで、販売数の大小に関わらず、各商品の予測精度を公平に評価することができます。
ウェブサイトへのアクセス数を予測する場合も同様です。ある特定の日にアクセス数が急増するイベントがあると、RMSEではその日の予測誤差が全体の評価を大きく左右してしまいます。しかし、RMSLEを用いれば、イベントによるアクセス数の急増を適切に捉え、より安定した評価を行うことができます。
RMSLEのもう一つの利点は、突発的な値、いわゆる外れ値の影響を受けにくいことです。たとえば、商品の価格を予測する際に、通常よりも極端に高額な商品がデータに含まれているとします。RMSEを用いると、この高額商品の予測誤差が全体の評価に大きな影響を与えてしまい、モデルの真の性能を正しく評価できない可能性があります。しかし、RMSLEでは予測値と実際の値の対数を用いるため、外れ値の影響が軽減され、より安定した評価結果を得ることができます。このように、RMSLEはデータにノイズが多い場合でも、より信頼性の高い評価指標として利用できます。
まとめると、RMSLEは予測対象の規模が大きく変動する可能性がある場合や、データに外れ値が含まれる場合に有効な指標です。販売予測、アクセス数予測、価格予測など、様々な場面で活用することができます。
| 指標 | 特徴 | メリット | 適用例 |
|---|---|---|---|
| RMSLE (二乗平均平方根対数誤差) | 予測値と実際の値の比率に着目 予測値と実際の値の対数を用いる |
予測値と実際の値の規模に大きな差がある場合に有効 外れ値の影響を受けにくい 各商品の予測精度を公平に評価 |
商品の販売数予測 ウェブサイトへのアクセス数予測 商品の価格予測 |
対数の順番

二乗平均平方根対数誤差(RMSLE)を計算する際、予測値と正解値の対数の順番について疑問が生じることがあります。具体的には、「予測値の対数から正解値の対数を引く」のか、「正解値の対数から予測値の対数を引く」のか、どちらが正しいのかという問題です。結論から言うと、RMSLEの計算においては、どちらの順番を用いても最終的な結果は変わりません。
RMSLEは、予測値と正解値の対数の差を二乗したものの平均の平方根を求めることで計算されます。数式で表すと、√( Σ(log(予測値) – log(正解値))^2 / n ) となります。ここで重要なのは、差を二乗している点です。対数の差を二乗すると、その順番が逆になったとしても、結果は変わりません。例えば、(a – b)^2 と (b – a)^2 はどちらも a^2 – 2ab + b^2 と等しくなります。
対数の計算においても同様のことが言えます。予測値の対数から正解値の対数を引いた場合と、正解値の対数から予測値の対数を引いた場合では、得られる値の符号は反転しますが、二乗することで正の値となり、最終的なRMSLEの値には影響を与えません。そのため、計算の順番はRMSLEの結果に影響しないのです。
とはいえ、計算の一貫性を保つためには、どちらか一方の順番に統一することをお勧めします。チームで作業する場合や、異なる時期に計算を行う場合など、順番が混在していると混乱を招く可能性があります。また、統一された計算式を用いることで、コードの可読性も向上します。どちらの順番を選ぶかは任意ですが、一度決めたらそれを守り、一貫性を保つことが大切です。
| 計算方法 | 数式 | 結果 |
|---|---|---|
| 予測値の対数 – 正解値の対数 | (log(予測値) – log(正解値))^2 | 正の値 |
| 正解値の対数 – 予測値の対数 | (log(正解値) – log(予測値))^2 | 正の値 |
RMSLEの計算では、どちらの順番でも最終的な結果は同じになります。
まとめ

二乗平均平方根対数誤差(RMSLE)は、予測値と実際の値の比率に着目した評価指標です。これは、他の誤差指標、例えば二乗平均平方根誤差(RMSE)などとは異なる特徴を持っています。適切な評価指標を選ぶためには、予測したいデータの性質を理解することが重要です。そうすることで、より効果的にモデルを評価できます。RMSLEは、極端に大きな値の影響を受けにくいという特性があります。これは、相対的な誤差を重視しているためです。そのため、特定の状況では非常に役立つ指標となります。例えば、売上高予測やウェブサイトへのアクセス数予測など、予測値の規模が大きく変わる可能性がある場合、RMSLEを使うことを考えてみる価値があります。
RMSLEは、予測値と実際の値の対数を用いて計算されます。このため、実際の値が小さい場合でも、予測値との比率が大きければ誤差も大きくなります。逆に、実際の値が大きい場合でも、予測値との比率が小さければ誤差も小さくなります。これは、RMSEのように絶対的な誤差を評価する指標とは大きく異なる点です。RMSEでは、実際の値が大きい場合、予測値との差が少し大きくても大きな誤差として扱われます。
例えば、ある商品の実際の売上高が10個で、予測値が20個だった場合を考えてみましょう。また、別の商品の実際の売上高が1000個で、予測値が1100個だった場合も考えてみます。RMSEでは、後者の誤差の方が大きく評価されます。しかし、RMSLEでは、前者の誤差の方が大きく評価されます。これは、前者の予測値は実際の値の2倍であるのに対し、後者の予測値は実際の値の1.1倍だからです。このように、RMSLEは相対的な誤差を重視するため、予測値の規模が大きく変動するデータに適していると言えます。
まとめると、RMSLEは予測値と実際の値の比率に着目した評価指標であり、大きな値の影響を受けにくく、相対的な誤差を重視するという特性があります。売上高予測やアクセス数予測など、予測値の規模が大きく変動する可能性がある場合には、RMSLEを用いることで、より適切なモデル評価を行うことができます。
| 評価指標 | 説明 | 特徴 | 適切なケース |
|---|---|---|---|
| RMSLE (二乗平均平方根対数誤差) | 予測値と実際の値の比率に着目した評価指標 |
|
|
| RMSE (二乗平均平方根誤差) | 予測値と実際の値の差の二乗平均の平方根 | 絶対的な誤差を評価 | – |
