RMSE:予測精度を測る指標

AIを知りたい
先生、『RMSE』(Root Mean Squared Error)ってどういう意味ですか?

AIエンジニア
Root Mean Squared Errorの訳の通り、二乗平均平方根誤差のことだね。簡単に言うと、機械学習モデルの予測値と正解値との間のずれの大きさを測る指標の一つだよ。

AIを知りたい
ずれの大きさ…ですか?もう少し詳しく教えてください。

AIエンジニア
たとえば、ある果物の重さを予測するモデルを作ったとしよう。実際の重さが100gの果物に対して、モデルが102gと予測した場合、誤差は2gだね。RMSEは、このような誤差を二乗して平均を取り、最後に平方根をとることで計算される。二乗する理由は、誤差のプラスマイナスを無視して、ずれの大きさを重視するためだよ。そして、たくさんのデータで誤差を評価するために平均を取り、最後に平方根を取ることで、元の誤差と同じ単位で評価できるようになるんだ。
RMSEとは。
人工知能の分野でよく使われる「RMSE」という言葉について説明します。これは、統計学や機械学習で使われるもので、平均してどれくらい予測が外れているかを表す指標です。このずれは、本来の値から予測値を引いても、予測値から本来の値を引いても構いません。
二乗平均平方根誤差とは

二乗平均平方根誤差(にしじょうへいきんへいほうこんごさ)とは、予測した値と実際の値との間の違いを測る尺度のことです。たとえば、ある製品の来月の売上高を予測するモデルを作ったとします。このモデルを使って予測した売上高と、実際に来月になったときに観測された売上高の間には、当然ながら差が生じるでしょう。この差が小さいほど、モデルの予測精度が高いと言えます。二乗平均平方根誤差は、まさにこの差を数値化し、モデルの良し悪しを判断するために使われます。
具体的には、まず予測値と実測値の差を計算し、それを二乗します。二乗する理由は、差が正負どちらであっても、その大きさを評価するためです。もし二乗しなければ、正の差と負の差が相殺されてしまい、全体の誤差を正しく評価できません。次に、二乗した差を全て足し合わせ、データの個数で平均を取ります。これにより、データ全体における平均的な誤差が分かります。最後に、この平均値の平方根を計算します。平方根を取ることで、元のデータと同じ単位で誤差を評価できるようになります。
二乗平均平方根誤差は、特に連続値を予測する問題(回帰問題)でよく使われます。例えば、売上予測や株価予測、気温予測などです。この尺度は、誤差が大きいデータの影響を大きく受けるという特徴があります。つまり、外れ値に敏感な尺度と言えるでしょう。これは、誤差を二乗することで、大きな誤差がより強調されるためです。もし外れ値の影響を小さくしたい場合は、代わりに平均絶対誤差などの別の尺度を用いると良いでしょう。
二乗平均平方根誤差は、値が小さいほど予測精度が高いことを示します。ゼロであれば、予測値と実測値が完全に一致していることを意味します。しかし、現実のデータでは誤差がゼロになることはほとんどありません。重要なのは、複数のモデルを比較する際に、二乗平均平方根誤差の値が小さいモデルの方が予測精度が高いと判断できることです。
| 用語 | 説明 |
|---|---|
| 二乗平均平方根誤差(RMSE) | 予測値と実測値の差を測る尺度。値が小さいほど予測精度が高い。 |
| 計算方法 | 1. 予測値と実測値の差を計算 2. 差を二乗 3. 二乗した差を全て足し合わせ、データの個数で平均を取る 4. 平均値の平方根を計算 |
| 使用場面 | 連続値を予測する問題(回帰問題) 例:売上予測、株価予測、気温予測 |
| 特徴 | 外れ値(誤差が大きいデータ)の影響を大きく受ける。 |
| 代替尺度 | 平均絶対誤差など |
計算方法

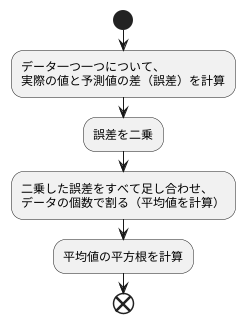
計算方法は、予測の正確さを測るための手順です。この手順は、いくつもの段階に分かれています。まず、集めたデータ一つ一つについて、実際の値と予測した値の差を計算します。この差が、どれくらい予測が外れていたかを示す「誤差」です。次に、計算した誤差をそれぞれ二乗します。二乗する理由は二つあります。一つは、誤差を常に正の値にするためです。正負が混ざっていると、全体の誤差を正しく把握しにくくなります。もう一つは、大きな誤差の影響をより大きく反映させるためです。小さな誤差は二乗してもあまり変化しませんが、大きな誤差は二乗すると非常に大きな値になります。これにより、大きな誤差が全体の結果に与える影響を強めることができます。それから、二乗した誤差をすべて足し合わせ、データの個数で割ります。これは二乗誤差の平均値を求める計算です。この平均値によって、全体の誤差の大きさを一つの数値で表すことができます。最後に、計算した平均値の平方根を計算します。平方根を計算することで、元の誤差と同じ尺度で全体の誤差を評価できます。これらの計算手順をまとめて式で表すと、データの個数を「n」、実際の値を「正解値i」、予測した値を「予測値i」とした場合、√(1/n * Σ(正解値i – 予測値i)^2) となります。ここで、Σは合計を表し、iはデータ一つ一つにつけた番号を表します。この計算方法によって得られた数値が、予測の正確さを示す指標となります。
解釈と活用

解釈と活用について説明します。
二乗平均平方根誤差(RMSE)は、予測値と実際の値との間のずれを測る指標です。このずれは、モデルがどれくらい正確に予測できているかを判断するのに役立ちます。RMSEの値が小さいほど、予測値と実際の値の差が小さく、モデルの予測精度が高いことを示します。
RMSEは、異なるモデルの性能を比較する際に非常に役立ちます。例えば、同じデータに対して複数の予測モデルを作成した場合、RMSEの値が最も小さいモデルが最も精度の高いモデルと判断できます。それぞれのモデルでRMSEを計算し、その値を比較することで、最適なモデルを選択できます。
RMSEは、モデルの改良にも活用できます。モデルの様々な設定を調整することで、RMSEの値がどのように変化するかを観察できます。例えば、予測モデルに用いる変数を変えたり、モデルの構造を調整したりすることで、RMSEの値がどのように変化するかを確認できます。RMSEの値が小さくなるように設定を調整することで、モデルの精度を向上させることができます。
RMSEの値をあらかじめ設定した基準値と比較することで、モデルの性能が十分かどうかを判断することもできます。もしRMSEの値が基準値よりも大きい場合は、モデルの精度が不十分であると判断し、更なる改良が必要になります。基準値は、予測を行う目的やデータの特性などを考慮して設定する必要があります。
このように、RMSEはモデルの評価や改良に活用できる重要な指標です。RMSEを正しく理解し、活用することで、より精度の高い予測モデルを構築することが可能になります。
| RMSEの役割 | 説明 |
|---|---|
| 予測精度の測定 | 予測値と実測値のずれを測り、モデルの予測精度を示す。RMSE値が小さいほど、精度は高い。 |
| モデル比較 | 複数のモデルのRMSE値を比較し、最も小さいRMSEを持つモデルが最も精度が高いと判断できる。 |
| モデル改良 | モデルの設定変更によるRMSE値の変化を観察することで、RMSE値が小さくなるようにモデルを調整し、精度を向上させる。 |
| モデルの性能評価 | RMSE値を基準値と比較し、モデルの性能が十分かどうかを判断する。基準値は、予測目的やデータ特性を考慮して設定する。 |
他の指標との比較

予測の良し悪しを測る尺度は、二乗平均平方根誤差(RMSE)以外にもたくさんあります。それぞれに良さがあるので、組み合わせて使うことで、モデルの性能を様々な角度から調べることができます。ここではRMSE以外の代表的な指標をいくつか紹介します。
まず、平均絶対誤差(MAE)について説明します。これは、実際の値と予測値の差の絶対値を取り、その平均を計算したものです。絶対値を使うため、RMSEのように大きな誤差が過大に評価されることはありません。つまり、MAEは外れ値の影響を受けにくい指標と言えるでしょう。RMSEとMAEを比較することで、モデルがどの程度外れ値に敏感なのかを知ることができます。
次に、決定係数(R^2)について説明します。R^2は、モデルがデータのばらつきをどのくらい説明できるかを表す指標です。0から1の間の値を取り、1に近いほどモデルがデータによく合っていることを示します。R^2は、モデルがどれだけ全体的な傾向を捉えているかを評価する際に役立ちます。ただし、R^2が高いからといって、必ずしもモデルが優れているとは限りません。データ量が少ない場合や、モデルが複雑すぎる場合は、R^2が高くても過学習を起こしている可能性があります。
最後に、これらの指標をどのように使い分けるかについて説明します。RMSEは、大きな誤差を小さくすることに重点を置きたい場合に適しています。例えば、工場の機械の故障予測など、大きな誤差が大きな損失につながる場合に有効です。一方、MAEは外れ値の影響を受けにくいため、安定した予測を重視する場合に適しています。例えば、日々の商品の売り上げ予測など、外れ値に左右されずに安定した予測を得たい場合に有効です。R^2は、モデルの全体的な適合度を評価したい場合に適しています。例えば、経済指標の予測など、全体的な傾向を捉えることが重要な場合に有効です。これらの指標を組み合わせて使用することで、モデルの性能をより深く理解し、目的に合ったモデルを選択することができます。
| 指標名 | 説明 | 長所 | 短所 | 適した場面 |
|---|---|---|---|---|
| 平均絶対誤差 (MAE) | 実際の値と予測値の差の絶対値の平均 | 外れ値の影響を受けにくい | 大きな誤差を過小評価する可能性 | 安定した予測を重視する場合(例:日々の商品の売り上げ予測) |
| 二乗平均平方根誤差 (RMSE) | 実際の値と予測値の差の二乗の平均の平方根 | 大きな誤差を重視する | 外れ値の影響を受けやすい | 大きな誤差が大きな損失につながる場合(例:工場の機械の故障予測) |
| 決定係数 (R^2) | モデルがデータのばらつきをどのくらい説明できるかを表す指標 (0~1) | モデルの全体的な適合度を評価できる | データ量が少ない場合やモデルが複雑すぎる場合は過学習の可能性 | 全体的な傾向を捉えることが重要な場合(例:経済指標の予測) |
注意点

二乗平均平方根誤差(RMSE)を用いる際には、いくつかの注意点に留意する必要があります。まず、RMSEは扱う数値の範囲に大きく左右されるという点です。例えば、家の価格を予測するモデルと、鉛筆の長さを予測するモデルでは、扱う数値の範囲が大きく異なります。家の価格は数百万円から数億円という範囲であるのに対し、鉛筆の長さは数センチメートルから数十センチメートルという範囲です。これらのモデルでRMSEを計算すると、家の価格を予測するモデルの方がRMSEの値が大きくなる可能性が高いですが、これは単に扱う数値の範囲が大きいためであり、必ずしも家の価格を予測するモデルの精度が低いことを意味するわけではありません。異なる範囲の値を扱う複数のモデルを比較する場合、RMSEの値だけで単純に比較するのではなく、扱う数値の範囲も考慮に入れる必要があります。例えば、各モデルでRMSEを計算する前に、データを標準化するなどの工夫が必要です。
さらに、RMSEは予測値と実際の値との平均的なずれを表す指標であるという点にも注意が必要です。つまり、RMSEは全体的な予測精度を表す指標ではありますが、個々のデータの予測精度については詳しい情報を与えてくれません。例えば、あるモデルのRMSEが小さい場合でも、特定のデータに対しては大きな予測誤差が生じている可能性があります。個々のデータに対する予測精度を詳しく確認したい場合は、他の指標も併用することが重要です。例えば、予測値と実際の値とのずれを個々のデータについて確認したり、予測誤差の分布を確認したりすることで、より詳細な分析ができます。RMSEはあくまでも全体的な指標の一つであることを理解し、必要に応じて他の指標と組み合わせて使うことで、より精度の高いモデル構築が可能になります。
| RMSEの注意点 | 詳細 | 対策 |
|---|---|---|
| 数値の範囲の影響 | RMSEは数値の範囲に大きく影響されるため、異なる範囲の値を扱うモデルを単純に比較することはできない。 | データを標準化するなど、数値の範囲を揃える工夫が必要。 |
| 平均的なずれ | RMSEは予測値と実際の値の平均的なずれを表す指標であり、個々のデータの予測精度については情報を与えない。 | 個々のデータの予測精度を確認したい場合は、他の指標も併用する必要がある。例えば、予測値と実際の値のずれを個々のデータについて確認したり、予測誤差の分布を確認する。 |
まとめ

予測の良し悪しを測る物差しの一つに、平均平方二乗誤差の平方根というものがあります。これは、よくRMSEと呼ばれています。このRMSEは、作った予測のモデルがどれくらい実際の値に近いのかを数字で表してくれるので、モデルの精度を評価する上でとても大切な指標です。
RMSEを正しく理解し、うまく使うことで、より精度の高い予測モデルを作ることができます。RMSEの値が小さいほど、予測値と実際の値のズレが小さいことを示し、モデルの精度が高いことを意味します。例えば、来月の売上高を予測するモデルを作ったとします。RMSEが小さいほど、そのモデルによる予測値が実際の来月の売上高に近いと期待できます。
しかし、RMSEには注意点もあります。RMSEは、扱うデータの大きさによって値が変わってしまう性質があります。例えば、家の価格を予測するモデルと、鉛筆の価格を予測するモデルでは、扱うデータの大きさが全く違います。そのため、RMSEだけを比較して、どちらのモデルの精度が高いと判断するのは難しい場合があります。また、RMSEは全体の平均的な誤差を表す指標なので、個々のデータの予測精度がどれくらい良いのかは分かりません。全体としてはRMSEが小さくても、特定のデータについては大きく外れている可能性もあります。
より確実にモデルを評価するためには、RMSEだけでなく他の指標も合わせて使うことが大切です。それぞれの指標は異なる側面からモデルの精度を評価しています。複数の指標を組み合わせて使うことで、モデルの弱点や改善点をより多角的に見つけることができます。例えば、平均絶対誤差(MAE)や決定係数(R²)といった指標も併用することで、より詳細な分析が可能になります。これらの指標と合わせてRMSEを使うことで、より良い予測モデルを作ることが期待できます。
機械学習の世界では、RMSEは非常によく使われる指標です。RMSEの計算方法やその意味を理解することは、予測モデルを作ったり評価したりする上で欠かせない知識と言えるでしょう。より精度の高い予測モデルを作るためには、RMSEを正しく理解し、他の指標と組み合わせて活用していくことが重要です。
| 指標名 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| RMSE (平均平方二乗誤差の平方根) | 予測のモデルがどれくらい実際の値に近いのかを数字で表す指標。値が小さいほど、予測値と実際の値のズレが小さい。 | モデルの精度を評価する上で大切な指標。 |
|
| MAE (平均絶対誤差) | 予測値と実測値の差の絶対値の平均。 | 外れ値の影響を受けにくい。 | |
| R² (決定係数) | モデルがどれくらいデータを説明できているかを表す指標。 | モデルの適合度を評価できる。 |
