リッジ回帰:滑らかなモデルを作る

AIを知りたい
先生、『リッジ回帰』って、重回帰分析に何かを足しているんですよね?どんなものを足しているんですか?

AIエンジニア
そうですね。リッジ回帰では、重回帰分析の目的関数に、パラメータ(重み)の二乗和を足しています。これをL2正則化と言います。

AIを知りたい
パラメータの二乗和を足すことで、どうなるんですか?

AIエンジニア
パラメータの二乗和を足すことで、一部のデータに引っ張られすぎるのを防ぎ、モデルを滑らかにします。つまり、過学習を防ぐ効果があるのです。ただし、完全に重みをゼロにはしないので、モデルが複雑になりやすいという欠点もあります。
リッジ回帰とは。
人工知能で使われる言葉、「リッジ回帰」について説明します。リッジ回帰とは、たくさんの要素が絡み合う関係を分析する「重回帰分析」という手法を、より安定させるための方法です。具体的には「L2正則化」という技術を使います。L2正則化とは、分析の目標となる関数に、分析に使う数値(重み)の二乗の合計を足し込むことを意味します。こうすることで、他のデータと比べて極端に違うデータの影響を少なくし、分析結果を滑らかにします。つまり、一部の特殊なデータに引っ張られて、偏った分析結果が出るのを防ぎます。ただし、データの影響を完全に無くすわけではないので、分析の仕組みが複雑になりやすい欠点もあります。
リッジ回帰とは

リッジ回帰は、重回帰分析を発展させた手法で、予測の正確さを上げるために用いられます。重回帰分析では、説明する変数と説明される変数の関係を直線で表しますが、扱うデータによっては、特定の変数に必要以上に合わせてしまうことがあります。これは、あるデータだけに特化しすぎて、新しいデータに対する予測の正確さが下がることを意味します。リッジ回帰は、この過剰適合と呼ばれる問題を防ぐための工夫が施されています。
具体的には、予測のための数式を作る際に、変数の影響の大きさを示す重み(係数)の大きさを制限します。重回帰分析では、この重みが大きくなりすぎる場合があり、これが過剰適合の原因の一つです。リッジ回帰では、重みを小さく抑えることで、特定の変数に過度に依存することを防ぎ、より汎用的な数式を作ることができます。この重みを調整する度合いは、正則化項と呼ばれる値で調整します。正則化項が大きければ重みはより小さく抑えられ、小さければ重みは比較的大きく、重回帰分析に近くなります。
結果として、新しいデータに対しても安定した予測が可能になります。特に、説明変数の数が多い場合や、説明変数間に強い相関がある場合に有効です。重回帰分析では、このような状況で過剰適合が起きやすく、予測精度が不安定になる可能性が高まります。リッジ回帰は、これらの問題を軽減し、より信頼性の高い予測モデルを構築するのに役立ちます。また、リッジ回帰は計算方法も比較的簡単であるため、広く利用されています。
| 項目 | 説明 |
|---|---|
| 手法 | リッジ回帰(重回帰分析の拡張) |
| 目的 | 予測精度の向上、過剰適合の防止 |
| 重回帰分析の問題点 | 特定の変数に過剰適合し、新しいデータへの予測精度が低下 |
| リッジ回帰の工夫 | 正則化項を用いて重み(係数)の大きさを制限 |
| 正則化項 | 重みを調整する度合いを決める値。大きいほど重みは小さく、小さいほど重みは大きく(重回帰分析に近い) |
| リッジ回帰の効果 | 新しいデータに対しても安定した予測が可能。特に説明変数の数が多い場合や強い相関がある場合に有効 |
| 利点 | 計算が比較的簡単 |
正則化という考え方

「正則化」とは、統計や機械学習において、モデルが学習データに過剰に適合することを防ぐための工夫のことです。まるで、起伏の激しいでこぼこ道を、平坦で走りやすい道路に整備する作業に似ています。でこぼこ道をそのまま進むと、一見すると地面にぴったりと沿っているように見えますが、実際には無駄な動きが多く、快適に進むことは難しいでしょう。同様に、複雑すぎるモデルは、学習データの個々の点に過度に適応しすぎてしまい、新しいデータに対する予測精度が落ちてしまうことがあります。これを「過剰適合」と呼びます。
正則化は、この過剰適合を防ぎ、モデルをより汎用性の高いものにするために用いられます。具体的には、モデルの複雑さを示す指標にペナルティを科すことで実現します。リッジ回帰では、モデルの重みの二乗和をペナルティとして用います。重みとは、各説明変数が予測値にどれくらい影響を与えるかを示す数値です。この重みの値が大きければ大きいほど、モデルは複雑になり、過剰適合しやすくなります。そこで、重みの二乗和を大きくすることでペナルティを課し、重みを小さい値に抑えるように仕向けます。
リッジ回帰では、モデルの誤差を最小化する関数である「目的関数」に、重みの二乗和を加えます。この目的関数を最小化することで、モデルの誤差を小さくしつつ、同時に重みの値も小さく保つことができます。結果として、過剰適合を防ぎ、新しいデータに対しても高い予測精度を持つモデルを構築することが可能になります。これは、でこぼこ道を滑らかに舗装することで、安定した走行を可能にすることと似ています。正則化は、モデルを安定させ、より実用的なものにするための重要な技術といえます。
| 用語 | 説明 | アナロジー |
|---|---|---|
| 正則化 | モデルが学習データに過剰に適合することを防ぐ工夫。モデルの複雑さにペナルティを科すことで、過剰適合を防ぎ、汎用性を高める。 | 起伏の激しいデコボコ道を、平坦で走りやすい道路に整備する作業。 |
| 過剰適合 | モデルが学習データの個々の点に過度に適応しすぎてしまい、新しいデータに対する予測精度が落ちてしまう現象。 | デコボコ道をそのまま進むと、地面にぴったりと沿っているように見えるが、実際には無駄な動きが多く、快適に進むことは難しい。 |
| リッジ回帰 | 正則化の一種。モデルの重みの二乗和をペナルティとして用いることで、重みを小さい値に抑え、過剰適合を防ぐ。 | デコボコ道を滑らかに舗装することで、安定した走行を可能にする。 |
| 重み | 各説明変数が予測値にどれくらい影響を与えるかを示す数値。重みが大きいほどモデルは複雑になり、過剰適合しやすくなる。 | – |
| 目的関数 | モデルの誤差を最小化する関数。リッジ回帰では、この関数に重みの二乗和を加える。 | – |
L2正則化の特徴

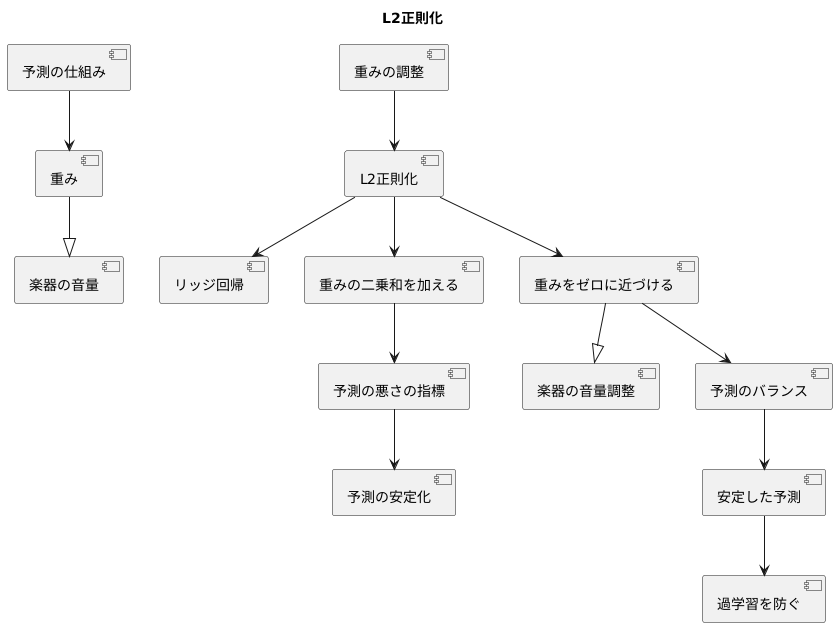
たくさんの種類がある予測の仕組みでは、学習を通じて予測に役立つ数値を調整します。この数値を重みと呼びます。この重みを調整する過程は楽器の音量を調整する過程に例えることができます。それぞれの楽器の音量が大きすぎると、曲全体のバランスが崩れてしまいます。同じように、重みの値が大きすぎると、予測結果が不安定になることがあります。
そこで、重みの値を調整する方法として、L2正則化という手法が用いられます。これは、リッジ回帰という予測方法で使われる大切な考え方です。L2正則化では、重みの値を二乗したものの合計を、予測の悪さの指標に加えます。この指標は、予測がどれだけ実際の値からずれているかを表すもので、この値が小さいほど良い予測と言えます。ここに重みの二乗和を加えることで、重みが大きくなりすぎないように調整します。
L2正則化の重要な点は、重みを完全にゼロにするのではなく、ゼロに近い小さな値にすることです。すべての楽器の音量をゼロにしてしまうと、曲は何も聞こえなくなってしまいます。しかし、それぞれの楽器の音量を小さく調整することで、全体の調和がとれて美しいハーモニーが生まれます。L2正則化も同様に、すべての重みを考慮に入れつつ、重要度の低い重みを小さくすることで、予測のバランスを取り、安定した予測を可能にします。つまり、少しづつすべての重みを調整することで、オーケストラ全体のハーモニーを作り出すように、予測結果全体のバランスを整えるのです。
このように、L2正則化は、重みの大きさを調整することで、より安定した予測を実現するための重要な手法と言えるでしょう。具体的には、過学習と呼ばれる、学習用のデータだけに最適化されすぎてしまい、未知のデータに対して予測精度が落ちてしまう現象を防ぐ効果があります。
リッジ回帰の欠点

尾根回帰は、統計学や機械学習の分野で広く使われている強力な手法ですが、いくつかの弱点も抱えています。その中でも特に重要なのが、不要な説明変数をモデルから完全に取り除くことができないという点です。
尾根回帰は、予測の誤差を小さくすると同時に、モデルの複雑さを抑えるために、正則化と呼ばれる仕組みを用います。具体的には、各説明変数に対応する重みの二乗和を罰則項として加えることで、重みが大きくなりすぎるのを防ぎます。この方法をL2正則化と呼びます。
L2正則化は、重みをゼロに近づける効果がありますが、完全にゼロにすることはありません。つまり、実際に予測に役立っていない説明変数であっても、モデルの中に残ってしまうのです。これは、料理を作る際に、すべての材料を少しずつ使うようなものです。味が複雑になり、どの材料が味に影響を与えているのか分からなくなります。同様に、尾根回帰では、多くの変数がモデルに残ってしまうため、どの変数が本当に重要なのかを判断するのが難しく、モデルの解釈性を低下させます。
この問題を解決する方法の一つとして、投げ縄回帰と呼ばれる手法があります。投げ縄回帰は、L1正則化と呼ばれる別の正則化方法を用います。L1正則化では、重みの絶対値の和を罰則項として加えます。この方法では、不要な説明変数の重みを完全にゼロにすることができるため、モデルから不要な変数を効果的に取り除くことができます。結果として、モデルが簡素化され、解釈しやすくなります。料理の例で言えば、使わない材料は完全に除外するため、味がすっきりとして、どの材料が重要なのかがはっきりと分かります。このように、目的に応じて適切な手法を選択することが重要です。
| 手法 | 正則化 | 罰則項 | 特徴 | 利点 | 欠点 |
|---|---|---|---|---|---|
| 尾根回帰 | L2正則化 | 重みの二乗和 | 重みをゼロに近づけるが、完全にゼロにはしない | 予測の誤差を小さくし、モデルの複雑さを抑える | 不要な説明変数を完全に取り除くことができないため、モデルの解釈性が低下する |
| 投げ縄回帰 | L1正則化 | 重みの絶対値の和 | 不要な説明変数の重みを完全にゼロにする | モデルが簡素化され、解釈しやすくなる | – |
リッジ回帰の利点

尾根回帰と呼ばれる手法は、様々な利点を持つ強力な予測分析手法です。まず第一に、計算手順が単純明快で、複雑な処理を必要としません。そのため、膨大な量の情報を扱う場合でも、比較的速やかに結果を得ることが可能です。これは、近年のデータ量の増大を考えると、非常に大きな強みと言えます。
第二に、尾根回帰は、予測モデルが学習データの特徴に過剰に適応してしまう「過学習」を防ぐ点で優れています。過学習が発生すると、未知のデータに対する予測精度が低下してしまいます。尾根回帰は、モデルのパラメータに制約を加えることで、この過学習を抑制し、未知のデータに対しても安定した予測を可能にします。
第三に、尾根回帰は、様々な場面で応用できる汎用性を備えています。例えば、お金に関する危険の予測や、病気の兆候を見つけるための診断支援、商品の販売戦略における顧客動向の分析など、幅広い分野で活用されています。それぞれの目的に合わせて、適切な設定を行うことで、高い予測精度を実現できます。
具体的には、尾根回帰は、モデルのパラメータの大きさに罰則を科すことで、過学習を抑制します。この罰則の強さを調整することで、モデルの複雑さを制御し、データの特性に最適な予測モデルを構築することができます。適切なパラメータ設定は、交差検証などの手法を用いて行います。このように、尾根回帰は、計算の容易さ、過学習への耐性、そして幅広い応用可能性を兼ね備えた、非常に有用な手法と言えるでしょう。
| 利点 | 説明 |
|---|---|
| 計算手順の簡潔さ | 複雑な処理を必要とせず、膨大なデータでも高速に処理可能。 |
| 過学習の抑制 | モデルパラメータに制約を加えることで、過学習を防ぎ、未知のデータに対しても安定した予測が可能。 |
| 幅広い応用可能性 | 金融リスク予測、医療診断支援、顧客動向分析など、様々な分野で活用可能。 |
パラメータ調整の重要性

機械学習のモデルを作る際には、まるで料理の味付けをするように、様々な要素を調整する必要があります。この調整を行う対象の一つが「パラメータ」と呼ばれるもので、モデルの働き方を細かく制御する役割を担っています。例えば、リッジ回帰という手法では、正則化と呼ばれる調整を行うためのパラメータが存在します。このパラメータは、モデルの複雑さと予測精度のバランスを調整する重要な役割を担っています。
このパラメータの値が小さすぎると、正則化の効果が弱まり、訓練データに過剰に適合してしまう現象が起こりやすくなります。これは、料理に例えると、特定の調味料を入れすぎてしまい、他の素材の味を殺してしまうようなものです。訓練データだけに最適化されたモデルは、新しいデータに対してはうまく予測できないため、実用性に欠けてしまいます。
逆に、パラメータの値が大きすぎると、モデルは単純化されすぎてしまい、データの中に含まれる重要な情報を見落としてしまう可能性があります。これは、料理の味付けが薄すぎて、素材本来の味が活かされていない状態に似ています。結果として、予測精度が低下し、望ましい結果を得ることができません。
最適なパラメータ値は、扱うデータの特性によって異なります。そのため、すべての状況に共通して使える万能な値は存在しません。料理のように、素材や好みに合わせて味付けを調整する必要があるように、データに合わせてパラメータを調整する必要があります。この調整を行うための有効な方法として、交差検証という手法があります。交差検証は、データを複数のグループに分け、それぞれのグループでモデルを訓練し、他のグループで性能を評価することで、最適なパラメータ値を探索する手法です。これにより、特定のデータに偏ることなく、より汎用的に使えるモデルを作ることができます。
| パラメータの値 | モデルの状態 | 料理の例え | 結果 |
|---|---|---|---|
| 小さすぎる | 正則化が弱く、過剰適合 | 特定の調味料を入れすぎて、他の素材の味を殺してしまう | 新しいデータへの予測精度が低い |
| 大きすぎる | モデルが単純化されすぎて、重要な情報を見落とす | 味付けが薄すぎて、素材本来の味が活かされていない | 予測精度が低い |
| 最適な値 | データの特性に最適化されたモデル | 素材や好みに合わせた適切な味付け | 汎用的に使えるモデル |
