リッジ回帰:過学習を抑える賢い方法

AIを知りたい
先生、「リッジ回帰」ってよく聞くんですけど、普通の線形回帰と何が違うんですか?

AIエンジニア
いい質問だね。線形回帰は、データにピッタリ合うように線を引くイメージだけど、リッジ回帰は線を少し滑らかにするんだ。ピッタリ合うようにしすぎると、新しいデータにうまく対応できないことがあるから、それを防ぐ工夫だよ。

AIを知りたい
滑らかにするって、具体的にはどうするんですか?

AIエンジニア
線を引く時の式の、それぞれの変数にかかる重みを小さくするように調整するんだ。重みが大きすぎると、その変数の影響が強くなりすぎて、線がデータに過剰に反応してしまう。リッジ回帰では、重みにペナルティを与えて、大きくなりすぎないようにするんだよ。だから、新しいデータにも対応しやすい、滑らかな線になるんだ。
リッジ回帰とは。
人工知能の分野でよく使われる「リッジ回帰」という手法について説明します。リッジ回帰は、線形回帰という基本的な予測手法を改良したものです。線形回帰は、データの関係を直線で表そうとするものですが、複雑なデータに合わせすぎると、新しいデータに対する予測精度が下がってしまうことがあります。これを「過学習」といいます。リッジ回帰は、過学習を防ぐために、予測に使う線の形を滑らかにする工夫を加えています。具体的には、線の形を決めるパラメータの値を小さく抑えることで、複雑すぎる線を防ぎ、より汎用的な予測モデルを作ることができます。
リッジ回帰とは

たくさんの情報から将来を予想することを目的とした計算方法の一つに、リッジ回帰というものがあります。
時折、集めた情報にぴったり合うように予想のやり方を覚えてしまうと、新しい情報に対してはうまく予想できないことがあります。
これは、いわば覚えることに集中しすぎて、応用する力が身についていない状態です。
このような状態を過学習と呼びます。リッジ回帰は、この過学習を防ぐための工夫です。
リッジ回帰は、基本的な予想方法である線形回帰を発展させたものです。
線形回帰は、データを直線で表すような単純な予想方法ですが、リッジ回帰は直線を少し曲げることで、より複雑な状況にも対応できるようにしています。
しかし、あまりに複雑にしすぎると、過学習を起こしてしまいます。
そこで、リッジ回帰は複雑さを調整する仕組みを導入しています。
具体的には、予想のやり方を決める要素(パラメータ)が大きくなりすぎないように制限を加えます。
この制限は、パラメータの大きさの二乗に比例する罰則として与えられます。
この罰則を正則化項と呼びます。
予想の精度は、集めた情報とのずれの小ささと、正則化項の大きさのバランスで決まります。
リッジ回帰は、ずれを小さくしつつ、パラメータが大きくなりすぎないように調整することで、過学習を防ぎ、新しい情報に対しても適切な予想ができるようになります。
このように、リッジ回帰は過学習を防ぎ、より確かな予想を立てるための優れた方法と言えるでしょう。
| 項目 | 内容 |
|---|---|
| 目的 | たくさんの情報から将来を予想 |
| 課題 | 過学習(集めた情報にぴったり合いすぎて、新しい情報にうまく対応できない) |
| 手法 | リッジ回帰 |
| リッジ回帰の仕組み | 線形回帰をベースに、パラメータの大きさに制限(正則化項)を加えることで過学習を防ぐ |
| 正則化項 | パラメータの大きさの二乗に比例する罰則 |
| 予想の精度 | 情報とのずれの小ささと正則化項の大きさのバランスで決まる |
| 効果 | 過学習を防ぎ、新しい情報に対しても適切な予想ができる |
線形回帰との違い

筋道立てて物事を説明する手法の一つに、線形回帰というものがあります。これは、様々なデータの関係性を直線で表そうとする試みです。例えば、気温の変化とアイスクリームの売上の関係を調べたい時、線形回帰を用いれば、気温が上がるとアイスクリームの売上も上がるという関係を直線で表現できます。
しかし、現実のデータは複雑で、単純な直線ではうまく表せない場合も少なくありません。データには、偶然によるばらつき(ノイズ)が含まれているからです。気温以外にも、天気や曜日、近隣のイベントなど、アイスクリームの売上に影響を与える要素はたくさんあります。線形回帰は、これらのノイズの影響も取り込んで直線を引こうとするため、結果として複雑に入り組んだ曲線になってしまうことがあります。これが過学習と呼ばれる現象です。過学習が起きると、学習に使ったデータにはよく合いますが、新しいデータにはうまく対応できません。
そこで登場するのが、リッジ回帰です。リッジ回帰は、線形回帰に改良を加えた手法です。線形回帰は、データに完全に合わせようとしますが、リッジ回帰は、あえて完全に合わせないように調整されています。具体的には、パラメータと呼ばれる値の大きさを制限する仕組みが組み込まれています。この仕組みのおかげで、リッジ回帰はノイズの影響を受けにくく、過学習を防ぐことができます。
線形回帰とリッジ回帰の違いを料理に例えてみましょう。線形回帰は、目の前にある食材を全て使い、複雑で手の込んだ料理を作るようなものです。確かに見栄えは良いかもしれませんが、味が濃すぎたり、特定の食材の味が強すぎたりするかもしれません。一方、リッジ回帰は、食材を厳選し、シンプルな味付けで素材本来の味を生かした料理を作るようなものです。見た目こそシンプルですが、誰にでも好まれるバランスの良い味に仕上がります。
このように、リッジ回帰は、線形回帰の欠点を補い、より現実に即した分析を可能にする手法と言えます。複雑なデータの背後にある真の関係を捉えるためには、リッジ回帰のような工夫が不可欠なのです。
正則化項の役割

機械学習において、モデルが訓練データに過剰に適合してしまう「過学習」は、しばしば問題となります。過学習したモデルは、訓練データにはよく適合しますが、未知のデータに対する予測性能が低くなってしまいます。この過学習を防ぐための強力な手法の一つが、正則化項の導入です。
正則化項は、モデルの複雑さを制御する役割を担います。モデルの複雑さとは、言い換えると、モデルがどれくらい自由にデータに適合できるかを表すものです。複雑すぎるモデルは、訓練データの細かな変動まで捉えようとしてしまい、結果として過学習を引き起こします。
正則化項は、モデルのパラメータの大きさに罰則を与えることで、この複雑さを抑制します。例えば、リッジ回帰という手法では、パラメータの値の二乗和を正則化項として用います。この正則化項は、損失関数と呼ばれる、モデルの予測精度を表す指標に加えられます。損失関数は、モデルの学習過程で最小化されるように調整されますが、正則化項が加わることで、パラメータの値が大きくなりすぎることを防ぎます。
損失関数を最小化しようとするモデルは、データへの適合度とパラメータの大きさのバランスを取ることを強いられます。結果として、モデルは訓練データの細かなノイズに過剰に反応することなく、全体的な傾向を捉えた滑らかな曲線で表現するようになります。
正則化項の強さは、調整可能な値であるハイパーパラメータによって制御されます。このハイパーパラメータは、モデルの複雑さと予測性能のバランスを調整する重要な役割を果たします。ハイパーパラメータの値を適切に設定することで、過学習を防ぎつつ、高い予測精度を実現することができます。最適なハイパーパラメータの値は、交差検証などの手法を用いて決定されます。
| 問題点 | 過学習:モデルが訓練データに過剰に適合し、未知データへの予測性能が低い |
|---|---|
| 解決策 | 正則化項の導入 |
| 正則化項の役割 |
|
| 正則化項の例 | リッジ回帰(パラメータの二乗和) |
| 損失関数 | モデルの予測精度を表す指標。正則化項が加えられる。 |
| モデルの学習 | 損失関数を最小化。データへの適合度とパラメータの大きさのバランスを取る。 |
| ハイパーパラメータ | 正則化項の強さを制御。交差検証などで最適値を決定。 |
ハイパーパラメータの調整

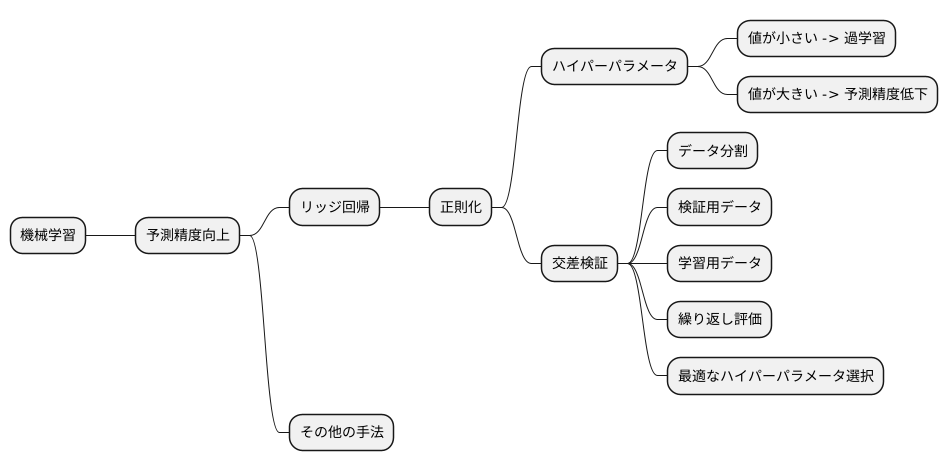
機械学習の分野では、予測の正確さを上げるために様々な工夫が凝らされています。その中でも、リッジ回帰はデータの特性を捉え、将来の予測に役立つ手法として知られています。リッジ回帰では、正則化と呼ばれる調整を行うことで、予測のずれを小さくする効果が期待されます。この正則化の強さを決めるのがハイパーパラメータであり、この値によってモデルの性能が大きく左右されます。ハイパーパラメータの値が小さすぎると、学習データの細かな特徴に過剰に適合してしまい、未知のデータに対する予測精度が低下する過学習と呼ばれる状態に陥ってしまいます。逆に、ハイパーパラメータの値が大きすぎると、学習データの特徴を十分に捉えられず、予測精度が低いモデルになってしまう場合があります。
そこで、最適なハイパーパラメータを見つけるために、交差検証と呼ばれる手法がよく用いられます。交差検証は、データを複数のグループに分割し、各グループを順番に検証用データとして用いることで、モデルの性能を評価する手法です。例えば、データを5つのグループに分割した場合、1つのグループを検証用データとし、残りの4つのグループを学習用データとしてモデルを学習します。学習後、検証用データを用いてモデルの予測精度を評価します。これを5回繰り返し、各グループが1回ずつ検証用データとなるようにすることで、モデルの性能をより正確に評価できます。
交差検証において、様々なハイパーパラメータの値を試すことで、どの値が最も高い予測精度を生み出すかを調べることができます。具体的には、ハイパーパラメータの値を少しずつ変化させながら、交差検証を行い、最も高い精度が得られた値を最適なハイパーパラメータとして採用します。このように、交差検証を用いてハイパーパラメータを調整することで、過学習を防ぎ、未知のデータに対しても高い予測精度を持つ、より信頼性の高いモデルを構築することが可能となります。これは、リッジ回帰に限らず、様々な機械学習手法で重要なステップとなります。
リッジ回帰の利点

リッジ回帰は、基本的な線形回帰に改良を加えた手法で、いくつかの点で優れた性質を持っています。まず、線形回帰では学習に使ったデータに過剰に適合してしまう、いわゆる過学習の問題が起こることがあります。過学習が起きると、学習に使ったデータにはよく当てはまるモデルができますが、新しいデータに対する予測の精度は低くなってしまいます。リッジ回帰では、モデルの複雑さを抑える仕組みが加えられているため、過学習を防ぎ、未知のデータに対しても高い予測精度を保つことができます。
次に、線形回帰を使う際に問題となるのが、説明変数間の強い相関、多重共線性です。説明変数とは、予測の根拠となる変数のことです。これらの変数間に強い相関があると、モデルのパラメータ、つまり変数の影響の大きさを示す値が不安定になり、正しい予測ができなくなることがあります。リッジ回帰では、正則化と呼ばれる手法を用いてパラメータの値を調整することで、多重共線性の影響を弱め、安定した予測を可能にします。具体的には、パラメータの大きな変動を抑えることで、モデルを安定化させています。
さらに、リッジ回帰は計算の手間が比較的少ないため、たくさんのデータを使った大規模な解析にも容易に適用できます。線形回帰と比べて計算時間が大幅に増えることもなく、計算資源の限られた環境でも利用しやすい手法と言えるでしょう。
これらの利点から、リッジ回帰は様々な分野で活用されています。例えば、経済学では経済指標の予測に、医学では病気のリスク予測に、工学では製品の品質管理にと、幅広い分野で役立っています。 線形回帰では対応が難しい状況でも安定した予測結果を期待できるため、データ分析を行う上で非常に強力な手法と言えるでしょう。
| 項目 | 説明 |
|---|---|
| 過学習抑制 | モデルの複雑さを抑えることで、過学習を防ぎ、未知のデータに対しても高い予測精度を保つ。 |
| 多重共線性への対応 | 正則化を用いてパラメータの値を調整し、多重共線性の影響を弱め、安定した予測を可能にする。 |
| 計算効率 | 計算の手間が比較的少ないため、大規模な解析にも容易に適用可能。 |
| 活用分野 | 経済学、医学、工学など、様々な分野で活用されている。 |
リッジ回帰の応用

尾根回帰と呼ばれる手法は、様々な分野で活用されています。具体例をいくつか見てみましょう。まず、お金に関する分野では、株の値動きを予想したり、危険性を評価したりする際に役立っています。将来の株価を予測することで、投資判断に役立てることができます。また、貸し倒れリスクなど、お金に関する様々な危険性を評価するのにも使われています。
次に、医療の分野での活用例です。尾根回帰は、病気の種類を見分けたり、治療の効果がどの程度期待できるかを予想したりするのに役立ちます。患者の様々なデータから病気を診断するだけでなく、治療の効果を予測することで、より適切な治療方針を立てることができます。
商品の販売促進に関わる分野でも、尾根回帰は活躍しています。顧客の買い物行動を予測することで、どんな商品を、どのように宣伝すれば効果的かを判断できます。例えば、過去の購入履歴やWebサイトの閲覧履歴などから、顧客が次にどんな商品に興味を持つのかを予測することができます。
さらに、近年注目を集めている画像認識や自然言語処理といった分野でも、尾根回帰の技術を応用した新しい方法が開発されています。画像に写っているものが何であるかを自動的に判断する画像認識や、人間が話す言葉をコンピュータに理解させる自然言語処理は、人工知能の重要な技術です。これらの技術の進歩にも、尾根回帰が貢献しています。
このように、尾根回帰は将来の値を予測する必要がある様々な場面で役立つ手法です。なぜ、こんなにも幅広く使われているのでしょうか?それは、尾根回帰が持つ二つの大きな特徴にあります。一つは、学習データに過剰に適応してしまうことを防ぐ能力が高い点です。もう一つは、安定して信頼できる予測結果を出せるという点です。これらの特徴のおかげで、尾根回帰は様々な分野で頼りにされているのです。
| 分野 | 活用例 |
|---|---|
| 金融 | 株価予測、リスク評価(貸し倒れリスクなど) |
| 医療 | 病気の診断、治療効果予測 |
| マーケティング | 顧客の購買行動予測、効果的な販売促進 |
| AI(画像認識、自然言語処理) | 画像認識、自然言語処理技術の向上 |
