残差平方和:モデルの精度を測る

AIを知りたい
先生、『RSS』って統計学とか機械学習で出てくる用語ですよね?よく耳にするんですけど、ちゃんと説明できません。教えてもらえますか?

AIエンジニア
はい。『RSS』は『残差平方和』のことで、機械学習などでモデルの良さを評価する際に用いられます。簡単に言うと、モデルの予測値と実際の値がどれだけズレているかを表す指標の一つです。それぞれのデータのズレを『残差』と言い、その残差を二乗して合計したものがRSSです。

AIを知りたい
残差を二乗するのはなぜですか?そのまま合計するだけではダメなのでしょうか?

AIエンジニア
いい質問ですね。残差をそのまま合計すると、プラスのズレとマイナスのズレが相殺されてしまう可能性があります。二乗することで、ズレの大きさを正の値で評価できるようになり、相殺を防ぐことができます。また、大きなズレをより重視することにも繋がります。ちなみに、残差を「観測値 – 予測値」と計算しても「予測値 – 観測値」と計算しても、二乗した結果は同じになります。
RSSとは。
人工知能に関わる言葉「RSS」について説明します。RSSとは、統計学や機械学習で使われるもので、残りの二乗和の値を計算して、その合計を出すためのものです。残りは、「実際に観測された値 – 予測された値」で計算されますが、「予測された値 – 実際に観測された値」で計算しても、結果は変わりません。
残差平方和とは

統計や機械学習の世界では、予測モデルの良し悪しを測る物差しが必要です。その物差しの一つに、残差平方和というものがあります。これは、モデルがどれほど観測データに合致しているかを表す数値です。この数値が小さいほど、モデルの予測精度は高いと判断できます。
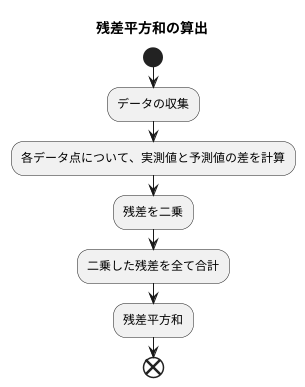
では、残差平方和とは具体的にどのように計算するのでしょうか。まず、個々のデータを見ていきます。ある時点での商品の実際の売上と、モデルが予測した売上の差を計算します。この差を残差と呼びます。残差はプラスの場合もあればマイナスの場合もあります。そのまま合計してしまうと、プラスとマイナスが打ち消し合ってしまい、全体のずれの大きさが正しく測れません。そこで、それぞれの残差を二乗します。二乗することで、すべての残差が正の値になり、打ち消し合いの問題がなくなります。これらの二乗した残差をすべて合計したものが、残差平方和です。
例えば、ある商品の来月の売上を予測するモデルを作ったとしましょう。過去の売上データとモデルを使って、来月の売上の予測値を計算します。そして実際に来月が終わった後に、実際の売上データが手に入ったら、予測値と実際の売上の差、つまり残差を計算します。それぞれの日の残差を二乗し、それを合計することで残差平方和が求まります。もし残差平方和が小さければ、モデルが日々の売上の変化をよく捉え、精度の高い予測ができていると解釈できます。逆に残差平方和が大きければ、モデルの予測精度が低いと考えられます。つまり、モデルが実際の売上の動きをうまく捉えられていないということです。このように、残差平方和はモデルの精度を評価する上で重要な指標となります。
計算方法と意味

残差平方和、これは統計の世界でモデルの良し悪しを測る物差しのようなものです。では、この物差しはどのように作られるのでしょうか。手順は大きく分けて三段階あります。まず、集めたデータ一つ一つについて、実際の値とモデルが予測した値の差を計算します。この差こそが「残差」と呼ばれるもので、モデルの予測がどれだけ外れたかを示しています。次に、それぞれの残差を二乗します。これは、プラスのずれもマイナスのずれも等しく評価するためです。最後に、二乗した残差を全て足し合わせます。これが残差平方和、つまりモデルと現実のデータとの間のずれの総和です。
この残差平方和は、小さければ小さいほど良いとされています。なぜなら、残差平方和が小さいということは、モデルの予測値と実際の値とのずれが小さい、つまりモデルが現実をよく説明できていることを意味するからです。残差平方和がゼロに近いということは、モデルがほとんど完璧に現実のデータを再現していることを示唆しています。まるで職人が寸分違わず設計図通りに作品を作り上げたようなものです。逆に、残差平方和が大きい場合は、モデルと現実のデータとの間に大きなずれがあることを意味し、モデルが現実をよく捉えられていない可能性を示しています。これは、設計図とは似ても似つかない作品が出来上がってしまったようなものです。例えば、商品の売れ行きを予測するモデルで残差平方和が大きい場合、商品の値段や季節といった売れ行きに影響を与える重要な要素がモデルに含まれていない、あるいはそもそもモデルの設計自体が間違っているといったことが考えられます。このような場合は、モデルを作り直したり、改善する必要があるでしょう。
残差の計算方法

残差とは、観測値と予測値の差を表す値です。言い換えると、ある現象を予測した際に、実際の観測値とのずれがどれくらいあるかを示す指標となります。この残差の計算方法には、「観測値から予測値を引く方法」と「予測値から観測値を引く方法」の二つのやり方がありますが、最終的に得られる残差平方和の値はどちらの方法でも変わりません。
なぜこのようなことが起こるのでしょうか?それは、残差平方和を計算する過程で、それぞれの残差を二乗するためです。例えば、あるデータの観測値が10、予測値が8だとします。観測値から予測値を引く方法で計算すると、残差は2となります。一方、予測値から観測値を引く方法を用いると、残差は-2となります。これらの残差をそれぞれ二乗すると、どちらも4という同じ値になります。つまり、残差平方和に及ぼす影響は同じなのです。
大切なのは、どちらの計算方法を選ぶかではなく、選んだ方法を分析を通して一貫して用いることです。プロジェクト全体で計算方法を統一することで、誤解や混乱を避けることができます。また、データ分析において再現性は非常に重要です。そのためにも、採用した残差の計算方法を明確に記録しておくようにしましょう。そうすることで、他の人が同じデータを使って分析を行う場合でも、同じ結果を得ることができ、分析結果の信頼性を高めることができます。
まとめると、残差の計算方法は二種類ありますが、残差平方和への影響は同じです。重要なのは、分析全体で計算方法を統一し、それを記録しておくことです。これにより、分析の正確性と再現性を確保し、より信頼性の高い結果を得ることが可能になります。
| 項目 | 説明 |
|---|---|
| 残差 | 観測値と予測値の差 |
| 計算方法1 | 観測値 – 予測値 |
| 計算方法2 | 予測値 – 観測値 |
| 残差平方和への影響 | どちらの計算方法でも同じ |
| 重要な点 | 分析全体で計算方法を統一し、記録しておく |
| 利点 | 分析の正確性と再現性を確保し、信頼性の高い結果を得られる |
他の指標との関係

残差平方和(ざんさへいほうわ)は、統計の分野で、モデルの良し悪しを測る物差しの一つであり、他の色々な統計指標と深く関わっています。残差平方和とは、観測値とモデルが予測した値との差、つまり残差を二乗して、全て足し合わせたものです。この値が小さいほど、モデルが実際のデータに良く合っていると考えられます。
例えば、決定係数(けっていけいすう)は、残差平方和を使って計算されます。決定係数は、一般的に「R-二乗」とも呼ばれ、モデルがデータのばらつきをどれくらい説明できるかを示す指標です。0から1までの値を取り、1に近いほどモデルの説明力は高く、データのばらつきをよく説明できていると解釈できます。具体的には、全体のばらつきから、モデルで説明できないばらつき(残差平方和に相当)を引いたものを全体のばらつきで割ることで計算されます。
また、平均二乗誤差(へいきんにじょうごさ)も残差平方和と関連の深い指標です。これは残差平方和をデータの個数で割って求められます。平均二乗誤差は残差の二乗の平均値であり、モデルの予測の精度を評価する際に用いられます。値が小さいほど、予測の精度は高いと言えます。
このように、残差平方和、決定係数、平均二乗誤差は互いに関連し、組み合わせて使うことでモデルの性能を様々な角度から評価することができます。例えば、残差平方和が小さくても、データの数が少ないと平均二乗誤差は大きくなることがあります。ですから、複数の指標を合わせて見ていくことで、より的確なモデル評価が可能となります。
| 指標 | 説明 | 計算方法 | 値の意味 |
|---|---|---|---|
| 残差平方和 | モデルの良し悪しを測る物差し。 | (観測値 – 予測値)^2 の合計 | 小さいほど、モデルがデータに良く合っている。 |
| 決定係数 (R-二乗) | モデルがデータのばらつきをどれくらい説明できるかを示す。 | 1 – (残差平方和 / 全体のばらつき) | 0 から 1 の値。1 に近いほどモデルの説明力は高い。 |
| 平均二乗誤差 | モデルの予測精度を示す。 | 残差平方和 / データの個数 | 小さいほど、予測の精度は高い。 |
モデル改善への活用

残差平方和は、統計の分野でモデルの良し悪しを測る大切な指標の一つです。この値は、観測値とモデルが予測した値との差を二乗した合計で表されます。この残差平方和をより小さくすることで、モデルの精度を高めることができます。
モデルを作る際には、様々な調整可能な変数(パラメータ)が存在します。これらのパラメータを調整することで、残差平方和を最小にすることができます。この手法は最小二乗法と呼ばれ、統計学の中でも基本的な手法として広く知られています。最小二乗法は、残差平方和を最小にするパラメータの組み合わせを探すための計算方法です。例えば、直線を表すモデル(線形回帰モデル)では、直線の傾きと切片がパラメータとなります。これらの値を調整することで、観測データに最もよく合う直線を求めることができます。
残差平方和が小さいほど、モデルが観測データをよく説明できていると考えられます。言い換えると、モデルの予測値と実際の観測値のずれが小さいことを意味します。ですから、残差平方和を最小にするパラメータを見つけることで、より精度の高いモデルを構築することが可能になります。
また、モデルを修正する前と後で残差平方和を比較することで、モデルの改善度合いを測ることもできます。モデルに変更を加えた後、残差平方和が小さくなっていれば、その変更は効果的であったと言えるでしょう。逆に、残差平方和が大きくなっている場合は、加えた変更が適切ではない可能性が高く、モデルの修正方法を再検討する必要があります。このように、残差平方和はモデルの改善に役立つ重要な指標です。
| 用語 | 説明 |
|---|---|
| 残差平方和 | 観測値とモデルの予測値の差の二乗和。モデルの良し悪しを測る指標。小さいほど良い。 |
| パラメータ | モデルの調整可能な変数。 |
| 最小二乗法 | 残差平方和を最小にするパラメータを探す手法。 |
| 線形回帰モデル | 直線を表すモデル。傾きと切片がパラメータ。 |
| 残差平方和の比較 | モデル修正前後の比較で改善度合いを測る。小さくなれば改善、大きくなれば再検討が必要。 |
