相対二乗誤差:モデル評価の新基準

AIを知りたい
先生、『相対二乗誤差』って、何ですか?よく分かりません。

AIエンジニア
そうだね、少し難しいね。『相対二乗誤差』は、機械学習でAIの予測がどれくらい正確かを測るためのものだよ。普通の二乗誤差と違って、実際の値と予測値の差を、実際の値で割ることで、値の大きさに影響されにくくした指標なんだ。

AIを知りたい
値の大きさに影響されにくいって、どういうことですか?

AIエンジニア
例えば、1000円を予測して100円ずれたら誤差は100円だよね。でも、10円を予測して10円ずれたら同じ100円の誤差でも、10円に対しては大きなずれになる。相対二乗誤差は、このずれを割合で考えるから、1000円と10円の予測のずれを比べることができるんだ。
相対二乗誤差とは。
人工知能の分野でよく使われる「相対二乗誤差」という用語について説明します。これは、統計学や機械学習で使われる評価値、あるいはその評価値を計算するための関数を指します。簡単に言うと、真の値と予測値のズレ(誤差)を、真の値との比率で表したものと言えるでしょう。これにより、もとの値の大きさが異なるデータ同士でも、予測の精度を比較しやすくなります。
はじめに

{機械学習というものは、学習した結果がどれくらい良いのかを測る方法が大切}です。そうでないと、せっかく作ったものが役に立つのかどうかわかりません。結果を測る方法はいろいろとありますが、今回は「相対二乗誤差」という方法について説明します。
この「相対二乗誤差」は、普通の二乗誤差と違って、データの大きさが違っても比べやすいという特徴があります。たとえば、大きさが全然違う二つのデータを比べることを考えてみましょう。普通の二乗誤差で比べると、大きい方のデータの影響が強すぎて、小さい方のデータの特徴がうまく捉えられないことがあります。しかし、「相対二乗誤差」では、それぞれのデータの大きさで調整を行うため、データの大小に関係なく、誤差を公平に評価できます。
もう少し詳しく説明すると、「相対二乗誤差」は、実際の値と予測値の差を二乗し、それを実際の値の二乗で割ったものです。この計算によって、データの大きさの影響が取り除かれ、異なる大きさのデータでも正しく比較できるようになります。たとえば、ある商品の売上の予測モデルを考えたとき、扱う商品の価格帯によって売上データの大きさが大きく異なる場合があります。高額商品と低価格商品を同じモデルで扱う場合でも、「相対二乗誤差」を用いることで、それぞれの商品の売上予測の正確さを公平に評価できます。
このように、「相対二乗誤差」は、様々な種類のデータに対して、モデルの性能を一貫して評価できる便利な道具です。特に、データの大きさが大きく異なる場合に有効な評価指標と言えるでしょう。
| 評価指標 | 説明 | メリット | 適用例 |
|---|---|---|---|
| 相対二乗誤差 | 実際の値と予測値の差を二乗し、それを実際の値の二乗で割ったもの | データの大きさが違っても比べやすい、データの大小に関係なく誤差を公平に評価できる | 商品の売上予測モデル(高額商品と低価格商品) |
二乗誤差との違い

予測の正確さを評価する尺度として、二乗誤差と相対二乗誤差があります。これらは似ていますが、大きな違いがあります。まず、二乗誤差から説明します。二乗誤差とは、実測値と予測値の差を二乗した値です。計算は単純で分かりやすいという長所があります。しかし、データの範囲によって値が大きく変わるという短所もあります。例えば、ある商品の来月の売上を予測するモデルを2つ考えます。1つ目のモデルは、売上が10000個と予測し、実際には10010個でした。誤差は10個です。2つ目のモデルは、売上が10個と予測し、実際には1個でした。誤差は9個です。二乗誤差で考えると、1つ目のモデルは10の二乗で100、2つ目のモデルは9の二乗で81です。この場合、二乗誤差は1つ目のモデルの方が大きく、予測の精度は低いように見えます。しかし、売上規模全体を考えると、1つ目のモデルの方がより正確な予測をしていると言えるでしょう。このような二乗誤差の短所を補うのが、相対二乗誤差です。相対二乗誤差は、二乗誤差を実測値で割ることで、誤差を相対的な値に変換します。1つ目のモデルの相対二乗誤差は、100を10010で割って約0.001です。2つ目のモデルの相対二乗誤差は、81を1で割って81です。このように、相対二乗誤差を計算すると、全体規模との関係を考慮した、より適切な予測精度の評価ができます。つまり、1つ目のモデルの方が2つ目のモデルより予測精度が高いことが分かります。このように、相対二乗誤差は、データの範囲に左右されない、より客観的な指標と言えるでしょう。
| 尺度 | 定義 | 長所 | 短所 | 例1 (予測:10000個、実測:10010個) |
例2 (予測:10個、実測:1個) |
|---|---|---|---|---|---|
| 二乗誤差 | (実測値 – 予測値)^2 | 計算が単純で分かりやすい | データの範囲によって値が大きく変わる | 100 | 81 |
| 相対二乗誤差 | 二乗誤差 / 実測値 | データの範囲に左右されない、より客観的な指標 | – | 約0.001 | 81 |
計算方法

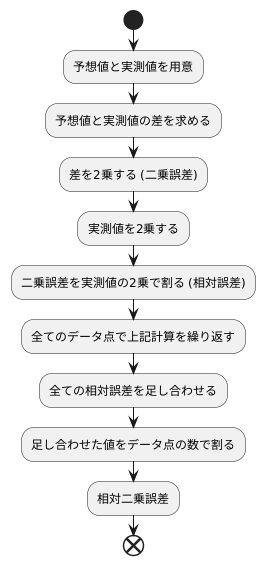
計算の手順を詳しく説明します。まず、ある事柄について、あらかじめ予想した値と実際に測って得られた値を用意します。この2つの値を使って計算を行います。最初のステップでは、予想した値と実際に測った値の差を求めます。この差は、予想がどれだけ外れていたかを示すものです。次に、求めた差を2乗します。2乗する理由は、差が正の数でも負の数でも、誤差の大きさを正の値で表すためです。この計算によって得られた値は、二乗誤差と呼ばれます。
次のステップでは、実際に測った値も2乗します。そして、最初のステップで計算した二乗誤差を、この実際に測った値の二乗で割ります。この計算によって、誤差を相対的な値に変換することができます。相対的な値とは、元の値に対する割合で表した値のことです。これにより、異なる大きさの値を比較することが容易になります。例えば、誤差が1で、実際に測った値が10の場合と、誤差が10で、実際に測った値が100の場合、どちらも相対的な誤差は0.1となり、同じ割合の誤差であることがわかります。
最後のステップでは、これまで説明した計算を全てのデータ点について行い、それぞれの相対誤差を全て足し合わせます。そして、足し合わせた値をデータ点の数で割って平均値を求めます。この平均値が相対二乗誤差です。相対二乗誤差は、全てのデータ点を考慮した平均的な誤差の大きさを示す指標となります。数式で表現すると、相対二乗誤差は、全てのデータ点における(予想値と実測値の差の二乗)の合計を、全てのデータ点における(実測値の二乗)の合計で割った値となります。ここで、合計は全てのデータ点を対象とすることを意味します。
活用事例

相対二乗誤差は、様々な分野で幅広く活用されています。その汎用性の高さから、予測モデルの精度評価において重要な役割を担っています。
まず、金融分野では、株価予測モデルの評価指標として用いられています。株価の変動は激しく、価格の範囲も広いため、通常の誤差では評価が難しい場合があります。しかし、相対二乗誤差を用いることで、変動の大きさに関わらず、予測の正確さを評価することができます。例えば、過去の株価データに基づいて学習したモデルが、将来の株価をどれだけ正確に予測できるかを評価する際に、この指標が役立ちます。
医療分野においても、相対二乗誤差は病気の診断予測モデルの評価に利用されています。例えば、患者の検査データや症状から、特定の病気を発症する確率を予測するモデルを開発する場合、そのモデルの精度を測るために相対二乗誤差が用いられます。診断結果の正確さが求められる医療分野では、信頼性の高い評価指標が必要とされ、相対二乗誤差はその役割を果たしています。
製造業においては、製品の品質予測モデルの評価に活用されています。製造工程における様々なデータ、例えば温度や圧力、材料の配合比率などから、最終製品の品質を予測するモデルを構築する際に、相対二乗誤差が重要な役割を担います。製品の品質は、企業の信頼性や収益に直結するため、予測モデルの精度は非常に重要です。相対二乗誤差を用いることで、モデルの予測精度を客観的に評価し、製造工程の改善に繋げることができます。
このように、相対二乗誤差は、データの規模に左右されずにモデルの性能を評価できるため、様々な分野で活用されています。これは、異なる規模のデータを持つ様々なモデルを比較評価する際に非常に有用です。相対二乗誤差を用いることで、より適切なモデルを選択し、予測精度を高めることが可能になります。
| 分野 | 活用例 |
|---|---|
| 金融 | 株価予測モデルの評価 |
| 医療 | 病気の診断予測モデルの評価 |
| 製造業 | 製品の品質予測モデルの評価 |
メリットとデメリット

相対二乗誤差は、機械学習モデルの性能を測る指標の一つであり、予測値と実測値の差を評価します。この指標には、長所と短所が存在するため、それらを理解した上で適切に利用することが重要です。長所としては、データの規模に左右されにくい点が挙げられます。例えば、ある製品の売上予測モデルを構築する場合、過去の売上データの規模が大きく変動していたとしても、相対二乗誤差を用いることで、モデルの性能を安定して評価することができます。つまり、異なる規模のデータを持つ複数のモデルを比較する場合でも、公平な評価が可能となるのです。これは、様々な状況下でモデルの性能を比較検討する際に非常に役立ちます。
一方、相対二乗誤差には、実測値が0に近い場合に値が非常に大きくなるという短所があります。例えば、ある希少な病気の発生率予測モデルを構築する場合、実測値である実際の発生率が非常に低い場合、わずかな予測誤差であっても相対二乗誤差は大きな値を示してしまう可能性があります。これは、モデルの性能を過小評価することに繋がるため、注意が必要です。このような場合は、相対二乗誤差だけでなく、他の指標も併用してモデルの性能を多角的に評価することが重要になります。例えば、正解率や適合率といった指標を合わせて用いることで、モデルの性能をより正確に把握することができます。また、実測値が全て0の場合は計算できないという点も留意すべき点です。つまり、全く発生しない事象を予測するモデルの場合、相対二乗誤差を用いて評価することができません。このような状況では、他の評価指標を選択する必要があるのです。このように、相対二乗誤差は便利な指標である一方、その特性を理解し、適切な場面で利用することが重要です。他の指標と組み合わせて使用することで、より精度の高いモデル評価を行うことができます。
| 指標 | 長所 | 短所 |
|---|---|---|
| 相対二乗誤差 | データの規模に左右されにくい 異なる規模のデータを持つ複数のモデルを比較する場合でも、公平な評価が可能 |
実測値が0に近い場合に値が非常に大きくなる 実測値が全て0の場合は計算できない |
まとめ

機械学習の分野では、作成した予測模型の良し悪しを測ることはとても大切です。そのためには、様々な評価方法が存在しますが、その中で相対二乗誤差は特に役立つ指標の一つです。この指標は、実測値と予測値の差を二乗し、それを実測値の二乗で割ることで計算されます。
相対二乗誤差を使う大きな利点は、異なる尺度のデータセットを比較できることです。例えば、ある商品の売上予測と、別の商品の広告費用予測のように、全く異なる単位や規模のデータであっても、相対二乗誤差を用いることで、それぞれの予測模型の精度を比較検討することが可能になります。これは、それぞれの値を同じ尺度に揃えることで実現されます。
しかし、相対二乗誤差を用いる際には注意点もあります。特に、実測値が零に近い場合、計算結果が非常に大きな値になる、もしくは計算自体が不可能になる可能性があります。これは、零で割ることができないという数学的な制約によるものです。このような状況では、相対二乗誤差は適切な指標とは言えず、他の評価方法を検討する必要があります。例えば、平均絶対誤差や平均二乗誤差などが挙げられます。
相対二乗誤差は単独で用いるよりも、他の指標と組み合わせて使うことで、より効果を発揮します。それぞれの指標は異なる側面から模型の性能を評価するため、複数の指標を総合的に判断することで、より多角的で正確な評価が可能になります。例えば、平均絶対誤差で全体的な誤差の大きさを把握し、相対二乗誤差でデータの尺度を考慮した誤差の割合を把握することで、模型の性能をより深く理解できます。
相対二乗誤差の性質や注意点、そして他の指標との組み合わせ方を理解し、適切に活用することで、より精度の高い予測模型を開発し、データに基づいた的確な判断を行うことが可能になるでしょう。
| 指標名 | 計算方法 | 利点 | 欠点 | 代替指標 |
|---|---|---|---|---|
| 相対二乗誤差 | (実測値 – 予測値)² / 実測値² | 異なる尺度のデータセットを比較できる | 実測値が0に近い場合、計算結果が非常に大きくなる、または計算不可能になる | 平均絶対誤差、平均二乗誤差 |
