相対絶対誤差:機械学習モデル評価の新基準

AIを知りたい
先生、「相対絶対誤差」ってよくわからないのですが、教えていただけますか?

AIエンジニア
いいですよ。「相対絶対誤差」は、AIがどれだけ予測を外したかを表す尺度の一つです。ただ、外れた量をそのまま使うのではなく、正解の値と比べてどれくらい外れたかを割合で見ています。たとえば、1000円のものを800円と予測した時と、10円のものを8円と予測した時では、どちらも200円/2円のずれですが、10円のものを予測した方がより大きく外れていると考えます。この考え方が「相対」という意味です。

AIを知りたい
なるほど。割合で考えるということですね。でも、なぜそんなことをする必要があるのですか?

AIエンジニア
良い質問ですね。それは、異なる大きさのものを予測する場合に、誤差を公平に比較するためです。例えば、1000円のものの予測と10円のものの予測を比べたいとき、そのままの誤差で比べると1000円のものの誤差の方が大きく見えてしまいます。でも、割合で考えると、どちらの予測がより精度が高いかを正しく評価できます。だから、色々なものの予測精度を比べたいときに「相対絶対誤差」は役に立つのです。
相対絶対誤差とは。
人工知能でよく使われる言葉「相対絶対誤差」について説明します。これは、統計学や機械学習で、予測の正確さを評価する数値、あるいはその数値を出すための計算方法です。本来の値と予測値の差(絶対誤差)を、相対的な値に変換したものです。この変換を行うことで、もとの値の大きさが異なるデータでも、予測の正確さを比較しやすくなります。
機械学習モデル評価の難しさ

機械学習の模型をきちんと吟味することは、模型作りにおいて大変大切なことです。けれども、色々な資料を使って学習させた複数の模型を比べたい場合、吟味の方法が適切でないと、間違った判断をしてしまうかもしれません。
例えば、ある模型は特定の資料に絞って高い能力を示す一方で、別の資料では低い能力しか示さないという状況はよくあります。これは、資料の特徴、例えば資料の範囲やばらつき、極端な値の有無などが、模型の能力に大きな影響を与えるためです。ある資料では、模型が資料の特徴をうまく捉え、高い精度で予測できるかもしれません。しかし、別の資料では、その資料の特徴が模型の学習内容と大きく異なっている場合、予測精度が下がるのも当然です。
このような、資料によって模型の能力が変わることを「過学習」と呼ぶこともあります。過学習が起きると、特定の資料に特化した模型になってしまい、新しい資料への対応力が低くなってしまいます。
真に使える模型を作るためには、色々な資料に対応できる能力、つまり汎化性能が重要になります。汎化性能の高い模型は、見たことのない新しい資料に対しても、高い精度で予測することができます。このような状況下で、模型の本当の能力を公平に吟味するためには、資料の特徴に左右されない、より幅広く使える吟味方法が必要です。
例えば、複数の資料を使って模型を吟味する方法や、資料を分割して学習と吟味に使う方法などがあります。これらの方法を適切に用いることで、より信頼性の高い模型の吟味が可能になります。そして、より良い模型を作り、実社会の様々な課題解決に役立てることができるのです。

相対絶対誤差:その役割と利点

予測値と実測値の差を評価する指標は様々ありますが、その中で相対絶対誤差は、異なる規模のデータセットを比較する際に特に役立ちます。まず、基本的な指標である絶対誤差について考えてみましょう。絶対誤差は、予測値と実測値の単純な差の絶対値で表されます。例えば、実際の気温が25度だった日に、ある予測モデルが28度と予測した場合、絶対誤差は3度となります。これは直感的で分かりやすい指標ですが、大きな問題点があります。それは、データの規模によって誤差の大きさが変わるため、異なるデータセット間での比較が難しいという点です。
例えば、100万円の住宅価格を予測するモデルと、100円の商品の価格を予測するモデルを考えてみましょう。住宅価格の予測モデルで1万円の誤差が生じた場合、これは比較的小さな誤差と言えるでしょう。しかし、商品の価格予測モデルで1万円の誤差が生じた場合、これは非常に大きな誤差です。このように、絶対誤差だけではモデルの性能を正しく評価できない場合があります。そこで、相対絶対誤差が登場します。相対絶対誤差は、絶対誤差を実測値で割ることで、誤差を相対的な値に変換します。先ほどの住宅価格の例で言えば、1万円の誤差を100万円で割ることで、相対絶対誤差は0.01、つまり1%となります。商品の価格予測モデルで同じ1万円の誤差が生じた場合、相対絶対誤差は100倍、つまり100%となります。このように、相対絶対誤差を用いることで、データの規模に左右されずにモデルの性能を評価することができます。つまり、住宅価格の予測モデルと商品の価格予測モデルを公平に比較することが可能になるのです。このため、異なる種類のデータセットを扱う際や、規模の異なるデータセットを比較する際には、相対絶対誤差が非常に有用な指標となります。
| 指標 | 計算方法 | 説明 | 例 |
|---|---|---|---|
| 絶対誤差 | |予測値 – 実測値| | 予測値と実測値の差の絶対値。データの規模によって誤差の大きさが変わるため、異なるデータセット間での比較が難しい。 | 実測値25度、予測値28度の場合、絶対誤差は3度。 |
| 相対絶対誤差 | |予測値 – 実測値| / 実測値 | 絶対誤差を実測値で割ることで、誤差を相対的な値に変換したもの。データの規模に左右されずにモデルの性能を評価できる。 |
|
計算方法と解釈

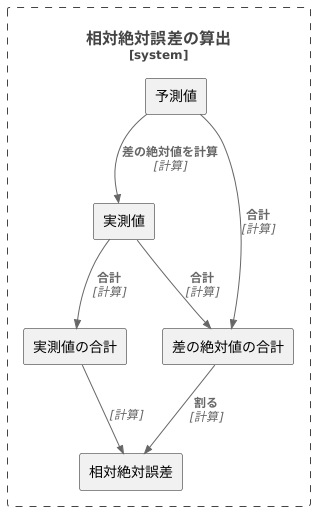
相対絶対誤差は、予測モデルの精度を評価する手法の一つで、計算も解釈も比較的簡単です。この指標は、予測値と実際の値がどの程度ずれているかを全体的な割合で示すものです。
まず、個々のデータ点について、予測値と実測値の差を計算します。この時、差が正負どちらであっても、その絶対値を用いることが重要です。全てのデータ点における絶対値のずれを合計することで、全体のずれの大きさを把握します。
次に、この全体のずれの合計値を実測値の合計値で割ります。これにより、ずれの大きさを実測値全体に対する割合として表すことができます。この割合が相対絶対誤差であり、値が小さいほど、予測値と実測値のずれが小さく、モデルの予測精度が高いと言えます。
例えば、相対絶対誤差が0.1だったとしましょう。これは、平均的に見て、予測値は実測値の10%以内の範囲に収まっていることを意味します。言い換えれば、実測値が100だとすると、予測値は90から110の間にあると期待できるということです。
しかし、注意点として、実測値の中に0が含まれている場合は、相対絶対誤差を計算することができません。これは、0で割ることができないという数学的な制約によるものです。このような場合は、他の評価指標を用いるか、データの処理方法を再検討する必要があります。相対絶対誤差は、実測値が全て正であるか、全て負である場合に有効な指標です。また、実測値のばらつきが大きい場合、相対絶対誤差は小さなずれを過大評価してしまう可能性があるため、データの特性を理解した上で適切に利用することが重要です。
他の評価指標との比較

機械学習の良し悪しを測るには、様々な方法があります。相対絶対誤差はその一つですが、他にも平均絶対誤差、平均二乗誤差、決定係数など、色々な尺度が存在します。それぞれの特徴を理解し、目的に合ったものを選ぶことが大切です。
相対絶対誤差は、データの規模が大きく異なる場合に特に役立ちます。例えば、ある製品の売上予測と、別の製品の売上予測を比較する場合、それぞれの売上の規模が全く違うかもしれません。このような場合、単純な誤差を比較するだけでは、どちらの予測が優れているかを正しく判断できません。相対絶対誤差は、それぞれのデータの規模を考慮に入れた上で誤差を計算するため、異なるデータセット間でのモデル比較に適しているのです。
一方で、相対絶対誤差には、極端に大きな値や小さな値、つまり外れ値の影響を受けやすいという弱点があります。もしデータの中に外れ値が含まれていると、相対絶対誤差の値が大きく歪められてしまう可能性があります。例えば、ほとんどのデータが予測値に近い値を取っているにも関わらず、一つだけ極端に大きな誤差を持つデータがあると、相対絶対誤差は非常に大きな値になってしまうかもしれません。このような場合は、外れ値の影響を受けにくい平均絶対誤差などを併用することで、より正確な評価を行うことができます。
それぞれの指標には長所と短所があるため、単一の指標だけでモデルの性能を判断するのではなく、複数の指標を組み合わせて総合的に判断することが重要です。目的に合わせて適切な指標を選び、多角的に評価することで、より信頼性の高いモデル構築が可能になります。
| 指標名 | 説明 | 長所 | 短所 |
|---|---|---|---|
| 相対絶対誤差 | データの規模を考慮に入れた誤差 | 異なるデータセット間でのモデル比較に適している | 外れ値の影響を受けやすい |
| 平均絶対誤差 | 誤差の絶対値の平均 | 外れ値の影響を受けにくい | – |
| 平均二乗誤差 | 誤差の二乗の平均 | – | – |
| 決定係数 | モデルの当てはまりの良さを示す指標 | – | – |
実践的な活用例

相対絶対誤差は、様々な分野で実用的に役立てられています。その活用例をいくつか詳しく見ていきましょう。
まず、お金に関する分野での活用例です。株価や為替の値動きを予想する数理模型を作る際には、その模型の良し悪しを評価する必要があります。この時、相対絶対誤差を用いることで、予想と実際の値のずれを、値の大きさに関わらず正しく評価できます。例えば、株価が大きく変動する時でも、小さく変動する時でも、同じ基準で模型の精度を測ることができます。
次に、医療の分野での例です。患者の今後の状態や病気の診断を助ける数理模型を作る際にも、相対絶対誤差は重要な役割を果たします。様々な検査値から、病気の可能性や重症度を予測する模型を作る場合、相対絶対誤差を用いることで、検査値の種類ごとに異なる単位や数値の範囲に影響されずに、模型の精度を評価できます。
製造業においても、相対絶対誤差は幅広く活用されています。製品の品質の良し悪しや、製品の需要を予測する模型を作る際に、相対絶対誤差を用いることで、異なる製品間で値の範囲が大きく異なる場合でも、模型の性能を適切に比較できます。例えば、小さな部品の寸法の誤差と、大きな機械全体の性能の誤差を比較する場合でも、相対的な誤差を評価することで、公平な比較が可能になります。
このように、相対絶対誤差は、データの大きさの違いに左右されないという利点があるため、様々な分野で活用されています。特に、異なる条件で学習させた複数の数理模型を比較する際には、相対絶対誤差を用いることで、より確かな評価を行うことができます。そのため、相対絶対誤差は、データ分析を行う上で、なくてはならない指標と言えるでしょう。
| 分野 | 活用例 | 相対絶対誤差の利点 |
|---|---|---|
| お金 | 株価や為替の値動き予測モデルの評価 | 値の大きさに関わらず、予想と実測のずれを正しく評価。株価の変動幅に関わらず、モデル精度を同じ基準で測定可能。 |
| 医療 | 患者の状態や病気診断予測モデルの評価 | 検査値の種類ごとの単位や数値範囲に影響されず、モデル精度を評価。 |
| 製造業 | 製品の品質や需要予測モデルの評価 | 製品間で値の範囲が大きく異なっても、モデル性能を適切に比較。小さな部品の寸法誤差と大きな機械の性能誤差も公平に比較可能。 |
今後の展望

機械学習という技術は日々進歩を続けており、これまで以上に複雑で高性能な予測モデルが次々と誕生しています。こうしたモデルの良し悪しを正確に見極めるためには、適切な評価指標を用いることが欠かせません。現在、相対絶対誤差は、データの規模に左右されないという点で、非常に有用な指標として広く活用されています。これは、例えば、ある商品の売上の予測において、売上の規模が大きく異なる複数の商品を比較する場合に、それぞれの予測精度を公平に評価できるということを意味します。しかし、相対絶対誤差には、極端に予測が外れた値、いわゆる外れ値の影響を大きく受けてしまうという弱点も抱えています。たとえば、ある商品の売上が通常100個であるにも関わらず、予測が1個だった場合、その誤差は非常に大きくなります。このような外れ値が一つでもあると、全体の評価が大きく歪んでしまう可能性があるため、注意が必要です。
今後の機械学習の発展においては、こうした外れ値の影響を受けにくい、より頑健な評価指標の開発が重要な課題となっています。具体的には、相対絶対誤差の欠点を補う、新たな指標の登場が期待されています。例えば、外れ値の影響を軽減するような計算方法を取り入れた指標や、外れ値を特定し、評価から除外する手法などが考えられます。また、単一の指標だけで評価するのではなく、複数の指標を組み合わせて多角的に評価する手法も重要です。例えば、予測の正確さを示す指標だけでなく、予測の安定性を示す指標なども併用することで、より包括的なモデル評価が可能になります。このように、機械学習技術の進歩と共に、評価指標も進化を続け、より精緻で信頼性の高いモデル評価を実現していくと考えられます。
| 機械学習の評価指標 | 説明 | 利点 | 欠点 |
|---|---|---|---|
| 相対絶対誤差 | データの規模に左右されずに予測精度を評価する指標 | 異なる規模のデータを公平に比較できる | 外れ値の影響を受けやすい |
| 今後の指標 | 外れ値の影響を受けにくい、より頑健な指標 | 外れ値の影響を軽減 外れ値を特定し除外 複数の指標を組み合わせ |
開発が必要 |
