過学習を防ぐ正則化

AIを知りたい
先生、「正則化」ってよく聞くんですけど、難しくてよくわからないんです。簡単に教えてもらえませんか?

AIエンジニア
そうだね。「正則化」は、AIが学習しすぎるのを防ぐための工夫だよ。 例えば、たくさんの問題と答えをAIに覚えさせるとするね。AIは、その問題と答えにぴったり合うように一生懸命に学習するんだけど、時には一生懸命になりすぎて、覚えた問題しか解けなくなってしまうことがあるんだ。これを「過学習」と言うんだよ。

AIを知りたい
なるほど。それで、正則化はどうやって過学習を防ぐんですか?

AIエンジニア
AIが学習するときには、色々な計算をするんだけど、正則化は、その計算に少しだけ細工を加えて、AIが答えを覚えることに集中しすぎないようにするんだ。 例えるなら、たくさんの問題を解くときに、答えを丸暗記するだけじゃなくて、ちゃんと考えながら解くように仕向けるようなものだね。そうすることで、AIは覚えた問題だけでなく、初めて見る問題にも対応できるようになるんだよ。
正則化とは。
人工知能の言葉で「正則化」というものがあります。これは、学習の際に使う数式に新たな部分を加えることで、重みと呼ばれる値の範囲を狭めます。そうすることで、重みが学習に使ったデータだけに過剰に合わせられてしまうこと(過学習)を防ぎます。
正則化とは

機械学習では、コンピュータに大量のデータを与えて、データの中に潜むパターンを見つけ出させ、将来の予測に役立てます。この学習過程で、時にコンピュータは与えられたデータの特徴を捉えすぎるという問題が起こります。まるで、特定の問題集の解答だけを丸暗記する生徒のように、訓練データに過剰に適応しすぎてしまい、新しい問題にうまく対応できなくなるのです。これを過学習と呼びます。
この過学習を防ぐための有効な手段の一つが、正則化です。正則化は、モデルが学習データの細かな特徴に過度にこだわりすぎるのを防ぎ、より一般的なパターンを学習するように促します。例えるなら、問題集の解答を丸暗記するのではなく、問題の背後にある基本的な原理や解き方を学ぶように指導するようなものです。
具体的には、正則化はモデルの複雑さを抑えることで実現されます。モデルの複雑さは、多くの場合、モデル内部のパラメータの大きさで決まります。これらのパラメータは、学習データに合わせて調整される数値です。正則化は、これらのパラメータが大きくなりすぎるのを防ぎ、モデルが複雑になりすぎるのを抑制します。これは、モデルが学習データの些細なノイズや例外的な特徴にまで過剰に反応するのを防ぎ、より本質的なパターンを捉えるのに役立ちます。
正則化を用いることで、モデルは学習データだけに特化した特殊なモデルではなく、より汎用的なモデルになります。これにより、未知のデータに対しても安定して高い予測精度を維持することが可能になります。つまり、新しい問題に直面したときでも、適切な解答を導き出せる能力が向上するのです。
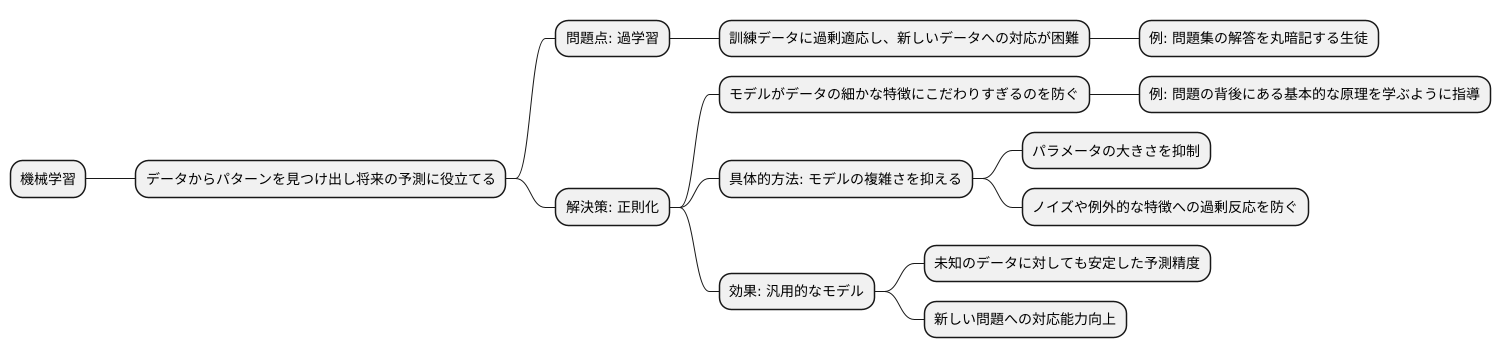
正則化の仕組み

機械学習モデルは、訓練データにあまりにも適応しすぎてしまい、未知のデータに対する予測精度が落ちてしまうことがあります。これを過学習といいます。過学習を防ぐための有効な手法の一つに、正則化があります。正則化とは、モデルの複雑さを抑えるための仕組みです。
具体的には、モデルの学習中に、損失関数に正則化項と呼ばれるペナルティを付け加えます。損失関数とは、モデルの予測と実際の値とのずれを表す指標で、この値を最小にするようにモデルは学習を進めます。ここに正則化項を加えることで、単に予測精度だけでなく、モデルの複雑さも考慮した学習を行うようになります。
正則化項は、モデルのパラメータの大きさをもとに計算されます。パラメータとは、モデル内部の調整可能な数値のことで、モデルの複雑さは、このパラメータの大きさで決まると考えることができます。パラメータの値が大きいほど、モデルは複雑になり、過学習しやすくなります。正則化項を加えることで、パラメータの値が大きくなるとペナルティが大きくなるため、学習アルゴリズムはパラメータの値を小さく抑えながら、損失関数を最小化しようとします。結果として、過学習しにくい、より汎化性能の高いモデルを作ることができます。
代表的な正則化手法には、L1正則化とL2正則化があります。L1正則化は、パラメータの絶対値の和を正則化項として用います。この方法の特徴は、重要でないパラメータをゼロにする傾向があることです。そのため、特徴選択の効果も期待できます。一方、L2正則化は、パラメータの二乗の和を正則化項として用います。L2正則化は、すべてのパラメータを滑らかに小さくする傾向があり、モデル全体を安定させます。どちらの手法も、パラメータの値を小さくすることで過学習を抑制しますが、その働き方に違いがあります。
このように、正則化は、モデルの複雑さを制御することで過学習を防ぎ、未知のデータに対しても高い予測精度を維持するための重要な手法です。
| 正則化手法 | 正則化項 | 特徴 |
|---|---|---|
| L1正則化 | パラメータの絶対値の和 | 重要でないパラメータをゼロにする傾向があるため、特徴選択の効果も期待できる。 |
| L2正則化 | パラメータの二乗の和 | すべてのパラメータを滑らかに小さくする傾向があり、モデル全体を安定させる。 |
正則化とは、モデルの複雑さを抑えるための仕組みです。モデルの学習中に、損失関数に正則化項と呼ばれるペナルティを付け加えることで、パラメータの値を小さく抑えながら損失関数を最小化し、過学習を防ぎます。
正則化の種類

機械学習において、モデルが訓練データに過剰に適合してしまう過学習を防ぐための手法の一つに、正則化があります。正則化は、モデルの複雑さを抑えることで、未知のデータに対する予測性能を向上させることを目指します。主な正則化の手法として、L1正則化とL2正則化の二種類があります。
L1正則化は、モデルのパラメータの絶対値の合計を損失関数に加える手法です。これを罰則項と呼びます。この罰則項によって、重要度の低いパラメータはゼロに近づき、結果としてモデルが単純化されます。つまり、いくつかのパラメータが完全にゼロになることで、特定の特徴量がモデルから完全に除外されることになります。そのため、L1正則化は特徴選択の効果も持ち合わせています。
一方、L2正則化は、モデルのパラメータの二乗の合計を損失関数に加える手法です。L1正則化と同様に、この罰則項もモデルの複雑さを抑える役割を果たします。ただし、L2正則化ではパラメータが完全にゼロになることは少なく、全てのパラメータが滑らかに縮小されます。この滑らかな縮小によって、モデルの過敏さを抑え、安定した予測を可能にします。
L1正則化とL2正則化は、それぞれ異なる特性を持っています。L1正則化は特徴選択に有効ですが、パラメータの値が急激に変化することがあります。L2正則化は安定した予測をもたらしますが、特徴選択の効果はあまり期待できません。そのため、扱うデータやモデルの特性に合わせて、どちらの手法を用いるか、あるいはどの程度の強さで正則化を適用するかを適切に選択する必要があります。
さらに、L1正則化とL2正則化を組み合わせたElastic Netと呼ばれる手法も存在します。これは、両方の正則化の効果をバランスよく取り入れることで、より柔軟なモデル構築を可能にします。状況に応じて、最適な正則化の手法を選択することで、モデルの性能を最大限に引き出すことができます。
| 手法 | 罰則項 | 効果 | 特徴 |
|---|---|---|---|
| L1正則化 | パラメータの絶対値の合計 | モデルの単純化、特徴選択 | 重要度の低いパラメータをゼロに、パラメータの値が急激に変化することがある |
| L2正則化 | パラメータの二乗の合計 | モデルの過敏さを抑制、安定した予測 | パラメータが滑らかに縮小、特徴選択の効果は低い |
| Elastic Net | L1正則化とL2正則化の組み合わせ | 両方の効果をバランスよく活用、より柔軟なモデル構築 | – |
正則化の利点

機械学習モデルを作る上で、過学習は常に付きまとう問題です。せっかく学習データで高い精度を出せても、新しいデータでは精度がガタ落ちしてしまうのでは意味がありません。そこで登場するのが正則化という手法です。正則化は、モデルが学習データの特徴に過剰に適合してしまうことを防ぎ、未知のデータに対しても高い予測性能を発揮できるように手助けしてくれます。
正則化の利点は、大きく分けて三つあります。まず第一に、汎化性能の向上です。正則化は、モデルのパラメータが大きくなりすぎるのを抑制することで、学習データの些細なノイズにまで過剰に反応することを防ぎます。これは、いわばデータの表面的な特徴ではなく、本質的な特徴を捉えることに繋がるため、新しいデータに対しても安定した予測が可能になります。
第二の利点は、モデルの解釈性の向上です。例えばL1正則化は、重要でない特徴量に対応するパラメータをゼロに近づける効果があります。これは特徴選択と同じ効果を持ち、どの特徴量が予測に重要な役割を果たしているかを判断しやすくなります。たくさんの特徴量から重要なものだけを選び出すことで、モデルの構造をより深く理解し、説明することが容易になります。
最後に、数値計算の安定性向上も正則化の利点です。パラメータの値が極端に大きくなると、計算が不安定になり、予測結果が信頼できないものになってしまうことがあります。正則化によってパラメータの値を適切な範囲に収めることで、数値計算の安定性を確保し、より信頼性の高いモデルを構築することができます。このように、正則化はモデルの性能向上に欠かせない重要な手法と言えるでしょう。
| 正則化の利点 | 説明 |
|---|---|
| 汎化性能の向上 | モデルパラメータが大きくなりすぎるのを抑制し、学習データのノイズへの過剰反応を防ぐ。新しいデータに対しても安定した予測が可能になる。 |
| モデルの解釈性の向上 | 重要でない特徴量に対応するパラメータをゼロに近づける(L1正則化)。どの特徴量が予測に重要か判断しやすくなる。 |
| 数値計算の安定性向上 | パラメータの値を適切な範囲に収め、計算の不安定化を防ぎ、信頼性の高いモデルを構築する。 |
正則化の適用例

様々な機械学習の手法で、正則化はモデルの精度を高めるために広く使われています。具体的な例をいくつか見てみましょう。まず、線形回帰では、予測を行う際に、たくさんの説明変数を使うことがあります。しかし、変数が多すぎると、学習データの細かい特徴にまで過剰に適合してしまい、新しいデータに対する予測精度が落ちてしまうことがあります。これを過学習と言います。このような場合、正則化を適用することで、モデルが学習データの特徴に過剰に適合することを防ぎ、新しいデータに対しても高い予測精度を維持することができます。
次に、ロジスティック回帰も、線形回帰と同様に、分類問題において広く使われている手法です。ロジスティック回帰でも、線形回帰と同様に過学習の問題が発生する可能性があります。正則化を適用することで、過学習を防ぎ、未知のデータに対しても安定した分類性能を達成できます。
サポートベクターマシンは、データの分類に用いられる手法で、データを分類する境界線を学習します。この境界線は、できるだけデータから離れた位置に設定することが望ましいのですが、正則化を用いることで、境界線の複雑さを調整し、過学習を防ぐことができます。
最後に、ニューラルネットワークは、人間の脳の仕組みを模倣した複雑なモデルです。多くの層とノードを持つため、表現力が高い反面、過学習しやすい性質も持ち合わせます。正則化は、ニューラルネットワークの過学習を抑え、汎化性能を向上させる上で重要な役割を果たします。画像認識や自然言語処理といった高度なタスクを扱う際に、正則化は特に重要になります。このように、正則化は、様々な機械学習モデルにおいて、モデルの複雑さを制御し、過学習を防ぎ、汎化性能を向上させるために不可欠な技術となっています。
| 機械学習手法 | 正則化の役割 |
|---|---|
| 線形回帰 | 過学習を防ぎ、新しいデータに対する予測精度を維持 |
| ロジスティック回帰 | 過学習を防ぎ、未知のデータに対する安定した分類性能を達成 |
| サポートベクターマシン | 境界線の複雑さを調整し、過学習を防ぐ |
| ニューラルネットワーク | 過学習を抑え、汎化性能を向上 |
正則化の注意点

正則化は、機械学習モデルの性能向上に役立つ強力な手法ですが、いくつかの注意点に気を配る必要があります。正則化を適切に用いるためには、その強さと種類を調整することが重要です。
まず、正則化の強さを調整する方法について説明します。正則化の強さは、モデルが学習データの特徴を捉える能力と過学習を防ぐ効果のバランスを保つ上で重要な役割を果たします。正則化の強さが適切に設定されていない場合、モデルの性能は大きく低下する可能性があります。具体的には、正則化が強すぎると、モデルは学習データの特徴を十分に学習できず、未学習の状態に陥ります。これは、モデルが単純になりすぎて、複雑なデータのパターンを捉えられないことが原因です。一方、正則化が弱すぎると、モデルは学習データに過剰に適合し、過学習が発生します。この場合、モデルは学習データには高い精度を示しますが、未知のデータに対する予測性能は低くなります。
適切な正則化の強さは、使用するデータやモデルによって異なり、事前に決めることは困難です。そのため、交差検証などの手法を用いて、最適な正則化の強さを探索することが重要です。交差検証では、学習データを複数の部分集合に分割し、それぞれを検証データとして用いることで、モデルの汎化性能を評価します。
次に、正則化の種類について説明します。代表的な正則化として、L1正則化とL2正則化が挙げられます。これらの正則化は、モデルのパラメータの値を小さくすることで過学習を防ぎますが、その働き方には違いがあります。L1正則化は、不要なパラメータの値をゼロにする効果があり、特徴選択に利用されることがあります。一方、L2正則化は、全てのパラメータの値を小さくする傾向があります。このように、L1正則化とL2正則化は異なる特性を持つため、データやモデルの特性に合わせて適切な種類を選択することが重要です。例えば、多くの特徴量の中から重要な特徴量を選び出したい場合は、L1正則化が効果的です。
正則化は強力な手法ですが、その効果を最大限に発揮するためには、強さと種類を適切に調整する必要があります。交差検証などの手法を用いて、データとモデルに最適な正則化の設定を見つけることが重要です。
| 項目 | 説明 |
|---|---|
| 正則化の強さ |
|
| 正則化の種類 |
|
