回帰問題:未来予測へのアプローチ

AIを知りたい
先生、「回帰問題」って、よく聞くんですけど、どんな問題のことなんですか?

AIエンジニア
いい質問だね。回帰問題とは、例えば、来月の売上高や、明日の気温といった、連続した値を予測する問題のことだよ。スーパーで、過去の売れ行きデータから、来月の牛乳の売上を予測する、といった状況を想像してみよう。

AIを知りたい
なるほど。連続した値を予測する問題ですね。じゃあ、商品の売れ行き予想以外にも、何か例はありますか?

AIエンジニア
他にも、株価の予測や、スポーツ選手の成績予測、降水量の予測など、様々な分野で使われているよ。要は、あるデータに基づいて、連続的な数値を予測したい時に、回帰問題を解くことになるんだ。
回帰問題とは。
人工知能で使われる言葉に「回帰問題」というものがあります。これは、例えば売上の予想のように、連続した値を予測する問題のことです。
回帰問題とは

回帰問題とは、入力データに基づいて連続した値の出力を予測する問題のことです。言い換えると、様々な要因から、ある数値がどれくらいになるのかを推測する手法と言えます。この数値は、整数や小数など、様々な値を滑らかに取ることができ、これを連続値と呼びます。 例えば、商店の明日の売上高を予測する状況を考えてみましょう。今日の売上や気温、近隣で行われるイベントの有無といった情報を入力データとして使用します。これらの情報に基づいて、明日の売上高という連続値を予測するのが回帰問題です。
売上高以外にも、様々な場面で回帰問題は活用されています。天気予報では、過去の気温や気圧、湿度などのデータから、未来の気温や降水量を予測します。株価予測では、企業の業績や経済指標、市場の動向といった情報から、将来の株価を予測します。また、顧客の購買行動の予測では、過去の購入履歴や閲覧履歴、顧客属性といったデータから、将来の商品購入確率を予測します。
これらの予測は、ビジネスにおける意思決定から科学的な研究まで、幅広い分野で役立っています。例えば、企業は売上高予測に基づいて生産量や在庫量を調整し、効率的な経営を行うことができます。また、科学者は回帰分析を用いて、実験データから法則や関係性を発見し、新たな知見を得ることができます。
このように、回帰問題は私たちの生活に深く関わっており、未来を予測し、より良い意思決定を行うための重要な手段となっています。様々な要因を考慮に入れ、複雑な関係性を分析することで、より精度の高い予測が可能になります。そして、その予測結果に基づいて行動することで、リスクを減らし、より良い結果を得ることができるのです。
| 問題の種類 | 説明 | 入力データの例 | 予測対象(出力) | 活用例 |
|---|---|---|---|---|
| 回帰問題 | 入力データに基づいて連続した値の出力を予測する問題 | 今日の売上、気温、近隣で行われるイベントの有無 | 明日の売上高 | 商店の売上予測、天気予報、株価予測、顧客の購買行動の予測 |
| 天気予報 | 過去の気温や気圧、湿度などのデータから、未来の気温や降水量を予測 | 過去の気温、気圧、湿度 | 未来の気温や降水量 | – |
| 株価予測 | 企業の業績や経済指標、市場の動向といった情報から、将来の株価を予測 | 企業の業績、経済指標、市場の動向 | 将来の株価 | – |
| 顧客の購買行動の予測 | 過去の購入履歴や閲覧履歴、顧客属性といったデータから、将来の商品購入確率を予測 | 過去の購入履歴、閲覧履歴、顧客属性 | 将来の商品購入確率 | – |
回帰問題の種類

様々な予測課題において、既知のデータから未知の値を推定する手法、つまり回帰手法は広く活用されています。回帰問題は、目的変数と説明変数の関係性をモデル化することで、新たな説明変数から目的変数を予測することを目指します。その関係性の形やモデルの複雑さによって、様々な種類の回帰問題が存在します。最も基本的な回帰問題として、線形回帰が挙げられます。線形回帰は、説明変数と目的変数の関係を直線で表すモデルです。この直線は、データに最もフィットするように、最小二乗法などの手法を用いて決定されます。線形回帰は、モデルの解釈が容易で計算コストも低いという利点があります。しかし、データの関係が直線でない場合には、予測精度が低くなる可能性があります。
データの関係が曲線で表される場合に有効なのが、多項式回帰です。多項式回帰は、説明変数を多項式で表現することで、より複雑な関係をモデル化できます。例えば、二次関数や三次関数を使って曲線を表現することで、線形回帰では捉えられない非線形な関係を表現できます。多項式回帰は、線形回帰よりも柔軟なモデルですが、次数が高くなると過学習のリスクも高まります。過学習とは、学習データに過度に適合し、未知のデータに対する予測精度が低下する現象です。
高次元データや複雑な関係を持つデータに対しては、サポートベクター回帰が有効な手法となります。サポートベクター回帰は、マージン最大化という考え方に基づき、データの境界線を最適に決定することで、高い予測精度を実現します。また、カーネル法と呼ばれる手法を用いることで、非線形な関係も効果的にモデル化できます。サポートベクター回帰は強力な手法ですが、計算コストが高く、パラメータ調整が複雑な場合もあります。
このように、回帰問題には様々な種類があり、それぞれ異なる特徴を持っています。どの手法が最適かは、扱うデータの特性や予測の目的に応じて異なります。そのため、最適なモデルを選択するためには、複数のモデルを試し、それぞれの性能を比較検討することが重要です。比較指標としては、決定係数や平均二乗誤差などが用いられます。また、交差検証法などを用いて、モデルの汎化性能を評価することも重要です。
| 回帰手法 | 説明 | 利点 | 欠点 | 適用場面 |
|---|---|---|---|---|
| 線形回帰 | 説明変数と目的変数の関係を直線で表す。 | 解釈が容易、計算コストが低い | データの関係が直線でない場合、予測精度が低い | データの関係が線形の場合 |
| 多項式回帰 | 説明変数を多項式で表現し、曲線で関係を表す。 | 線形回帰より柔軟、非線形関係を表現可能 | 次数が高いと過学習のリスク | データの関係が曲線の場合 |
| サポートベクター回帰 | マージン最大化で境界線を決定。カーネル法で非線形関係もモデル化可能。 | 高い予測精度、非線形関係もモデル化可能 | 計算コストが高い、パラメータ調整が複雑 | 高次元データ、複雑な関係を持つデータ |
回帰問題の評価指標

予測した値がどれくらい実際の値に近いかを確かめることは、回帰問題においてとても重要です。この「予測の良さ」を測るために、いくつかの方法があります。よく使われる方法として、平均二乗誤差、二乗平均平方根誤差、そして決定係数といったものがあります。
まず、平均二乗誤差について説明します。これは、予測値と実際の値の差を二乗し、その平均を求めたものです。それぞれの予測がどれくらい外れているかを二乗することで、大きなずれをより強く評価します。この値が小さいほど、予測がより正確であることを示します。
次に、二乗平均平方根誤差は、先ほどの平均二乗誤差の平方根をとったものです。平方根をとることで、元のデータと同じ単位で誤差を捉えることができます。例えば、売上の予測をしているなら、売上の単位と同じ「円」で誤差を考えられるので、より分かりやすくなります。
最後に、決定係数は、モデルがどれくらいデータの特徴を捉えているかを表す指標です。0から1までの値をとり、1に近いほど、モデルがデータをよく説明できていることを示します。これは、予測値が実際の値の変化をどれくらい説明できているかを表しています。
これらの指標を組み合わせて使うことで、モデルの良し悪しを多角的に評価できます。それぞれの指標が何を意味しているかを理解し、目的に合わせて適切な指標を選ぶことが、より良い予測モデルを作る上で重要です。
| 指標名 | 説明 | 特徴 |
|---|---|---|
| 平均二乗誤差 (MSE) | 予測値と実測値の差の二乗の平均 | 大きなずれをより強く評価 |
| 二乗平均平方根誤差 (RMSE) | MSEの平方根 | 元のデータと同じ単位で誤差を捉える |
| 決定係数 (R²) | モデルがデータの特徴を捉えているかを表す | 0から1の値を取り、1に近いほどモデルがデータをよく説明できている |
回帰問題の応用例

回帰問題とは、ある値とそれに関連する他の値との関係性を見つけ出し、その関係に基づいて未知の値を予測する手法です。この手法は、様々な分野で活用され、未来を予測する強力な道具となっています。
商業の分野では、商品の売れ行きを予測するのに役立ちます。過去の売れ行きデータや季節、景気、広告の効果といった様々な要因を分析することで、今後の売れ行きを予測し、仕入れや在庫管理に役立てることができます。また、顧客の購買行動を分析することで、顧客がどんな商品に興味を持っているのかを予測し、効果的な販売戦略を立てることができます。
医療の分野においても、回帰問題は重要な役割を果たしています。患者の症状や検査データ、過去の治療履歴などを分析することで、病気の診断を支援したり、治療の効果を予測したりすることができます。これにより、より適切な治療方針を決定し、患者の健康状態の改善に貢献することができます。
ものづくりにおいても、回帰問題の応用は広がっています。製品の製造過程で得られるデータから、製品の品質を予測し、不良品発生を未然に防ぐことができます。また、機械の稼働状況を監視し、故障の兆候を早期に発見することで、予知保全を実現し、安定した生産活動を維持することができます。
お金のやり取りの分野では、株価の変動予測やリスク評価に利用されています。過去の株価データや経済指標、企業の業績などを分析し、将来の株価の動きを予測することで、投資判断の材料とすることができます。また、顧客の信用情報や返済履歴などを基に、融資の可否や金利を決定する際にも、回帰問題が活用されています。
情報を広める活動においても、回帰問題は欠かせません。広告の効果を予測したり、顧客層を細分化したりすることで、より効果的な広告配信を実現できます。
このように、回帰問題は様々な分野で応用され、私たちの生活を豊かにするために役立っています。今後、データの蓄積と分析技術の進歩により、その応用範囲はさらに広がることが期待されます。
| 分野 | 回帰問題の活用例 |
|---|---|
| 商業 | 商品の売れ行き予測、顧客の購買行動分析に基づく販売戦略策定 |
| 医療 | 病気の診断支援、治療効果の予測 |
| ものづくり | 製品の品質予測、故障の兆候の早期発見(予知保全) |
| お金のやり取り | 株価変動予測、リスク評価、融資判断 |
| 情報を広める活動 | 広告効果予測、顧客層の細分化による効果的な広告配信 |
回帰問題を学ぶための方法

回帰問題とは、ある入力データから連続的な数値を予測する問題です。例えば、家の広さから価格を予測したり、過去の売上データから未来の売上を予測したりといった課題が、回帰問題にあたります。この問題を解くためには、統計学や機械学習の基礎を学ぶことが重要です。
まず、統計学の基礎知識として、確率、統計量、確率分布などを学ぶ必要があります。これらの知識は、データの性質を理解し、適切な分析手法を選択する上で欠かせません。次に、機械学習の基礎として、様々な回帰モデルについて学ぶ必要があります。代表的なモデルとしては、線形回帰、多項式回帰、サポートベクター回帰などがあります。それぞれのモデルの特徴や適用範囲を理解することで、より精度の高い予測が可能になります。
学習には様々な方法があります。入門書や専門書を読むことで体系的に学ぶことができます。最近は、インターネット上で無料の学習教材も数多く公開されています。動画講座やオンラインコースなども活用すると、より効率的に学ぶことができます。さらに、大学や専門学校で開講されている統計学や機械学習の講座を受講するという方法もあります。
プログラミング言語を学ぶことも重要です。特にPythonは、データ分析や機械学習の分野で広く使われており、豊富なライブラリが利用可能です。Pythonを使って、実際に回帰分析のプログラムを書いて、様々なデータセットで試してみることで、より深い理解を得ることができます。公開されているデータセットを使って練習することも効果的です。
機械学習の競技会に参加することも、実践的なスキルを磨く上で有効な手段です。競技会では、現実世界の問題を題材としたデータが提供され、参加者は予測モデルを構築して競い合います。他の参加者の解法やアイデアに触れることで、自身のスキル向上に繋がります。
回帰問題は、様々な分野で応用されている重要な技術です。継続的に学習し、実践を積み重ねることで、回帰問題の専門家を目指しましょう。学び続けることで、高度な手法を理解し、複雑な問題にも対応できるようになります。
| 項目 | 詳細 |
|---|---|
| 回帰問題とは | 入力データから連続的な数値を予測する問題。例:家の広さから価格予測、売上予測 |
| 必要な知識 | 統計学の基礎(確率、統計量、確率分布)、機械学習の基礎(線形回帰、多項式回帰、サポートベクター回帰など) |
| 学習方法 | 入門書、専門書、無料学習教材、動画講座、オンラインコース、大学/専門学校、プログラミング(Python)、データセット実践、機械学習競技会参加 |
| プログラミング言語 | Pythonが推奨。豊富なライブラリ、データ分析や機械学習に最適 |
| その他 | 継続的な学習と実践が重要 |
回帰問題の将来展望

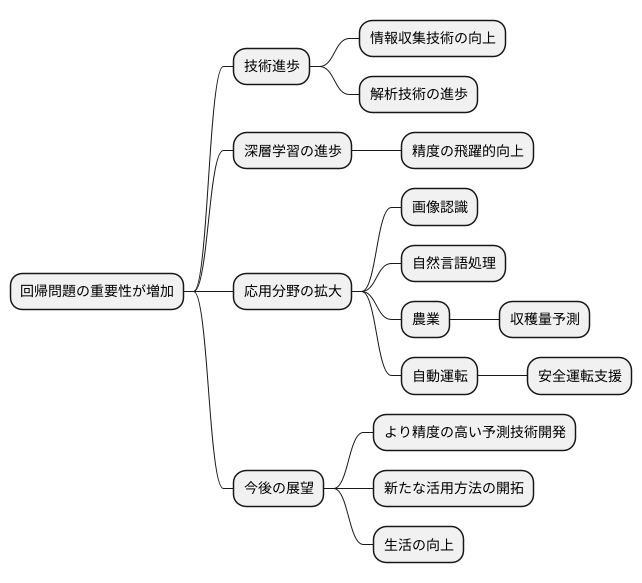
近頃では、多くの情報が集められ、それを細かく調べる技術も進歩しています。そのため、物事の関係性を数値で表す回帰問題の重要性は、今後ますます高まると考えられます。特に、人間の脳の仕組みをまねた深層学習の進歩によって、回帰問題の正確さは飛躍的に向上しています。
例えば、写真を見て何が写っているかを当てる画像認識や、人の言葉を理解する自然言語処理といった分野でも、回帰問題を使った研究が活発に行われています。これらの技術は、深層学習を取り入れることで、従来の方法よりも高い精度を達成しています。
さらに、身の回りのあらゆる物がインターネットにつながる技術の進歩により、様々な機械から情報が自動的に集められるようになりました。このおかげで、回帰問題が使える場面はさらに広がっています。例えば、最新の農業技術を使った収穫量の予想や、コンピューターが車を運転する自動運転技術などへの応用が期待されています。農業では、天気や土の状態などの情報を集めて、どれくらいの収穫が見込めるかを正確に予測することで、効率的な生産計画を立てることができます。自動運転では、周囲の状況を瞬時に判断し、安全な運転を支援するために回帰問題が活用されます。
このように、回帰問題は社会の様々な問題を解決するための大切な道具となるでしょう。より精度の高い予測技術の開発や、今までにない使い方の開拓など、回帰問題には無限の可能性が秘められています。今後、様々な分野で回帰問題が活用されることで、私たちの生活はより豊かで便利になることが期待されます。