決定係数R2:モデルの良さを測る

AIを知りたい
先生、「R2」ってなんですか?人工知能の分野でよく聞くんですけど、よくわかりません。

AIエンジニア
良い質問だね。「R2」は『決定係数』とも呼ばれ、機械学習モデルの予測精度を評価する指標の一つだよ。簡単に言うと、モデルがどれくらい実際のデータに合っているかを示す数値なんだ。

AIを知りたい
実際のデータに合っているか…ですか?もう少し具体的に教えてもらえますか?

AIエンジニア
例えば、アイスクリームの売上を気温から予測するモデルを作ったとしよう。R2が高いほど、そのモデルが気温の変化から売上の変化をよく説明できていることを意味するんだ。1に近いほど予測精度が高いとされていて、0に近いと予測が当たっていないことになるよ。
R2とは。
統計学や機械学習の分野で使われる「決定係数」という用語について説明します。この用語は「R2」とも呼ばれます。
決定係数とは

決定係数とは、統計の分野、特に回帰分析と呼ばれる手法において、作成した予測モデルの当てはまりの良さを評価するための指標です。この指標はよくRの2乗(R二乗)とも呼ばれ、一般的にはR2という記号で表されます。
回帰分析とは、ある値と別の値の関係性を数式で表す分析手法のことです。例えば、商品の広告費と売上の関係や、気温とアイスクリームの売上の関係などを分析するために用いられます。これらの関係性を数式で表すことで、将来の売上を予測したり、最適な広告費を決定したりすることが可能になります。
決定係数は、0から1までの値を取り、1に近いほどモデルが実際のデータによく合致していることを示します。仮に決定係数が1だった場合、モデルはデータのばらつきを完全に説明できている、つまり、予測が完璧であることを意味します。逆に決定係数が0に近い場合、モデルはデータのばらつきをほとんど説明できていないことを意味し、予測の精度は低いと言えます。
具体的に説明するために、商品の広告費と売上の関係を分析したとしましょう。もしこの分析で得られたモデルの決定係数が0.8だった場合、売上のばらつきの80%は広告費によって説明できるということを意味します。残りの20%は、広告費以外の要因、例えば景気の動向や競合他社の状況、商品の品質といった様々な要因によるものと考えられます。
決定係数は、モデルの良さを判断する上で重要な指標ですが、単独で判断材料とするのではなく、他の指標と合わせて総合的に判断することが大切です。また、決定係数はモデルが複雑になるほど高くなる傾向があるため、モデルの複雑さと決定係数のバランスを考慮する必要があります。複雑すぎるモデルは、一見するとデータによく合致しているように見えますが、将来の予測精度が低い可能性があるため注意が必要です。
| 指標名 | 別名 | 記号 | 意味 | 値の範囲 | 値の意味 |
|---|---|---|---|---|---|
| 決定係数 | Rの2乗(R二乗) | R2 | 予測モデルの当てはまりの良さ | 0 から 1 | 1に近いほど、モデルが実際のデータによく合致している |
| 決定係数の値 | 意味 |
|---|---|
| 1 | モデルはデータのばらつきを完全に説明できている(予測が完璧) |
| 0に近い | モデルはデータのばらつきをほとんど説明できていない(予測の精度は低い) |
| 0.8 | 売上のばらつきの80%は広告費によって説明できる。残りの20%は他の要因による |
| 注意点 |
|---|
| 単独で判断材料とするのではなく、他の指標と合わせて総合的に判断する |
| モデルが複雑になるほど高くなる傾向があるため、モデルの複雑さと決定係数のバランスを考慮する |
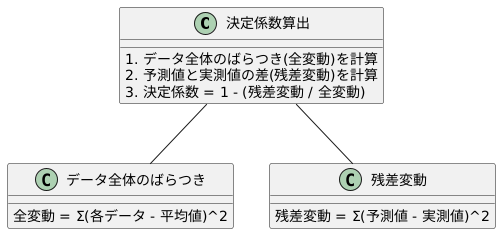
計算方法

計算方法は、予測の正確さを数値で示すために用いられます。具体的には、回帰分析という手法で得られた予測値が、実際の値とどれだけ近いかを測る指標の一つである決定係数の算出方法について説明します。
まず、データ全体のばらつきを計算します。これは全変動と呼ばれ、個々のデータの値と、全てのデータの平均値との差を二乗し、その合計を求めることで算出できます。この全変動は、データが平均値からどれくらい散らばっているかを示す指標となります。
次に、回帰分析によって得られた予測値と実際の値との差を計算し、それを二乗して合計を求めます。これは残差変動と呼ばれ、モデルが説明できなかったばらつきを示します。つまり、予測値が実際の値とどれくらいずれているかを表すものです。
最後に、決定係数を計算します。決定係数は、1から残差変動を全変動で割った値として求められます。言い換えると、全変動のうち、残差変動、つまり説明できなかったばらつきを除いた割合を計算することになります。この値は、0から1の間の値を取り、1に近いほど予測値が実際の値に近い、つまりモデルの精度が高いことを示します。例えば、決定係数が0.8だとすると、データ全体のばらつきの8割をモデルが説明できていると解釈できます。逆に、決定係数が0に近い場合は、モデルがあまりデータのばらつきを説明できていないことを意味します。
解釈と注意点

決定係数とは、統計モデル、特に回帰モデルがどれだけ観測データによく当てはまっているかを示す指標です。この値は、0から1までの範囲で表され、1に近いほどモデルがデータによく適合していることを示します。言い換えると、モデルがデータのばらつきをどれだけうまく説明できているかを表す数値と言えるでしょう。
しかし、決定係数の解釈には注意が必要です。高い決定係数が得られたとしても、必ずしもそのモデルが優れた予測力を持っているとは限りません。例えば、過学習と呼ばれる現象が起こると、モデルは学習に使ったデータには非常に良く適合しますが、新しいデータに対しては予測精度が低くなってしまいます。これは、まるで特定の問題の解答だけを暗記した生徒が、少し問題文が変わると途端に解けなくなってしまうような状況です。このようなモデルは、決定係数は高いものの、実用性は低いと言えます。
また、モデルの説明変数、つまり予測に使う要素の数を増やすほど、決定係数は高くなる傾向があります。これは、たくさんの要素を使えば、より複雑な現象も説明しやすくなるためです。しかし、要素を増やしすぎると、モデルがデータの個別の特徴にまで過剰に反応してしまい、かえって予測精度が低下することがあります。これは、細かすぎる情報を詰め込みすぎた結果、全体像が見えなくなってしまうようなものです。
したがって、モデルの良し悪しを判断する際には、決定係数だけに頼るのではなく、他の指標も併せて検討することが重要です。例えば、修正済み決定係数は、説明変数の数による影響を調整した指標であり、より客観的なモデル比較を可能にします。複数のモデルを比較する際には、修正済み決定係数を参考にすることで、過剰に複雑なモデルを選択してしまうことを避けることができます。
つまり、決定係数はモデルの適合度を評価する上で有用な指標ですが、その解釈には注意が必要であり、他の指標と組み合わせて総合的に判断することが大切です。
| 項目 | 説明 |
|---|---|
| 決定係数 | 統計モデルがどれだけ観測データによく当てはまっているかを示す指標。0から1までの範囲で、1に近いほどモデルがデータによく適合している。 |
| 決定係数の解釈の注意点 | 高い決定係数=優れた予測力ではない。過学習が発生すると、学習データへの適合度は高いが、新しいデータへの予測精度は低い。 |
| 説明変数の数と決定係数の関係 | 説明変数の数が増えると決定係数も高くなる傾向があるが、増やしすぎると過剰適合となり予測精度が低下する。 |
| 修正済み決定係数 | 説明変数の数による影響を調整した指標。より客観的なモデル比較が可能。 |
| 結論 | 決定係数は有用な指標だが、解釈には注意が必要で、他の指標と組み合わせて総合的に判断することが重要。 |
活用事例

決定係数という数値は、様々な分野で活用されています。この数値は、ある事柄が起こる理由を説明する際に、その説明がどれくらい正しいかを測る尺度となるため、幅広い分野で役立っています。
例えば、経済学の分野を考えてみましょう。経済学では、経済の動きを説明したり、将来の経済状況を予測したりするために、様々な数式モデルが用いられます。これらのモデルがどれくらい現実に即しているかを評価するために、決定係数が使われます。具体的には、株価の動きを予測するモデルや、人々の消費支出を予測するモデルなどが挙げられます。これらのモデルの決定係数が高いほど、モデルの予測精度が高いことを示しています。
また、医学の分野でも決定係数は活用されています。医学では、病気の原因を特定したり、病気のリスクを予測したりするために、様々な研究が行われています。これらの研究において、決定係数は、特定の要因(例えば、喫煙、食生活、運動習慣など)が病気の発症にどれくらい影響を与えているかを評価する際に役立ちます。例えば、特定の生活習慣から将来の心臓病リスクを予測するモデルを開発する場合、そのモデルの精度を評価するために決定係数が用いられます。
さらに、販売戦略を考えるマーケティングの分野でも、決定係数は重要な役割を果たしています。マーケティングでは、顧客の購買行動を理解し、将来の購買行動を予測するために、様々なデータ分析が行われています。顧客の年齢や性別、過去の購入履歴などの情報から、特定の商品を購入する可能性を予測するモデルを開発する際に、そのモデルの予測精度を評価するために決定係数が利用されます。決定係数が高いほど、モデルが顧客の購買行動をよく説明できていることを示し、効果的な販売戦略の立案に役立ちます。
| 分野 | 使用例 | 決定係数の役割 |
|---|---|---|
| 経済学 | 株価予測モデル、消費支出予測モデル | モデルの予測精度を評価 |
| 医学 | 病気のリスク予測モデル(例:心臓病リスク予測) | 特定の要因が病気の発症にどれくらい影響を与えているかを評価 |
| マーケティング | 顧客の購買行動予測モデル | モデルの予測精度を評価、効果的な販売戦略立案への貢献 |
他の指標との関係

決定係数は、統計モデルがどれくらいデータに適合しているかを示す指標ですが、単独で用いるよりも他の指標と組み合わせて使うことで、より深くモデルを評価できます。モデルの良し悪しを判断するには、様々な角度からの検討が必要です。
例えば、平均二乗誤差や平均絶対誤差といった指標は、予測値と実際の値の差がどれくらい大きいかを示すものです。これらの指標は、モデルの予測精度を評価する上で非常に重要です。平均二乗誤差は、差の二乗の平均を計算し、大きなずれをより強調する特徴があります。一方、平均絶対誤差は、差の絶対値の平均を計算し、外れ値の影響を受けにくいという特徴があります。これらの指標と決定係数を組み合わせることで、モデルがデータにどれくらい適合しているかと同時に、どれくらい正確に予測できているかを評価できます。適合度が高くても、予測精度が低いモデルは実用性に欠ける場合があるため、両者を合わせて検討することが重要です。
また、情報量基準やベイズ情報量基準といった指標は、モデルの複雑さと適合度のバランスを評価します。複雑すぎるモデルは、過学習と呼ばれる現象を起こし、見かけ上は適合度が高くても、新しいデータに対する予測精度が低い可能性があります。情報量基準やベイズ情報量基準は、このような過学習を防ぐために、モデルの複雑さにペナルティを科すことで、適切な複雑さのモデルを選択するのに役立ちます。これらの指標と決定係数を組み合わせることで、モデルの適合度だけでなく、複雑さも考慮した、より多角的なモデル評価が可能になります。つまり、単にデータへの当てはまりが良いだけでなく、将来のデータに対しても良い予測ができるモデルを選択できるようになります。
| 指標 | 説明 | 特徴 |
|---|---|---|
| 決定係数 | 統計モデルがデータにどれくらい適合しているかを示す | 単独ではなく他の指標と組み合わせて使う |
| 平均二乗誤差(MSE) | 予測値と実測値の差の二乗の平均 | 大きなずれを強調 |
| 平均絶対誤差(MAE) | 予測値と実測値の差の絶対値の平均 | 外れ値の影響を受けにくい |
| 情報量基準(AIC) | モデルの複雑さと適合度のバランスを評価 | 過学習を防ぐ |
| ベイズ情報量基準(BIC) | モデルの複雑さと適合度のバランスを評価 | 過学習を防ぐ |
