過学習を防ぐL2正則化

AIを知りたい
先生、「L2正則化」って、何だか難しそうなんですけど、簡単に説明してもらえますか?

AIエンジニア
そうだね、難しく感じるかもしれないね。簡単に言うと、L2正則化は、機械学習モデルが複雑になりすぎるのを防ぐ方法の一つだよ。 複雑になりすぎると、訓練データに過剰に適応してしまい、新しいデータに対してうまく予測できない「過学習」という状態になるんだ。L2正則化は、それを防ぐために、モデルのパラメータを小さくするように働きかけるんだよ。

AIを知りたい
パラメータを小さくする、というのはどういうことですか?

AIエンジニア
例えば、たくさんの数字を覚えることを想像してみて。重要な数字だけを覚える方が、細かすぎる数字まで全部覚えるよりも、新しい問題に柔軟に対応できるよね。L2正則化は、モデルにとって重要でないパラメータを小さくすることで、覚える数字を減らし、新しいデータにも対応できるようにしているんだ。だから、過学習を防いで精度を高めるのに役立つんだよ。
L2正則化とは。
人工知能にまつわる言葉、『L2正則化』について説明します。L2正則化とは、学習モデルが複雑になりすぎて、学習データだけに最適化され、新しいデータにうまく対応できなくなることを防ぐための方法の一つです。通常、このような調整は、損失関数と正則化項と呼ばれる二つの要素の和を最小にすることで行われます。L2正則化では、特に正則化項が、モデルのパラメータの二乗で表されます。似たような調整方法にL1正則化がありますが、L2正則化はL1正則化に比べて、新しいデータに対しても高い精度が出せる傾向にあります。現在、人気教育系動画投稿者である『ヨビノリ』さんと共同で、動画とブログによる解説コンテンツを公開中です。このコンテンツでは、人工知能の学習における重要な技術である正則化について、理論と実践の両面から学ぶことができます。詳しくは、下記のリンクをご覧ください。『予備校のノリで学ぶ「L1/L2正則化」:ヨビノリ&zerotooneコラボ企画第一弾』
正則化とは

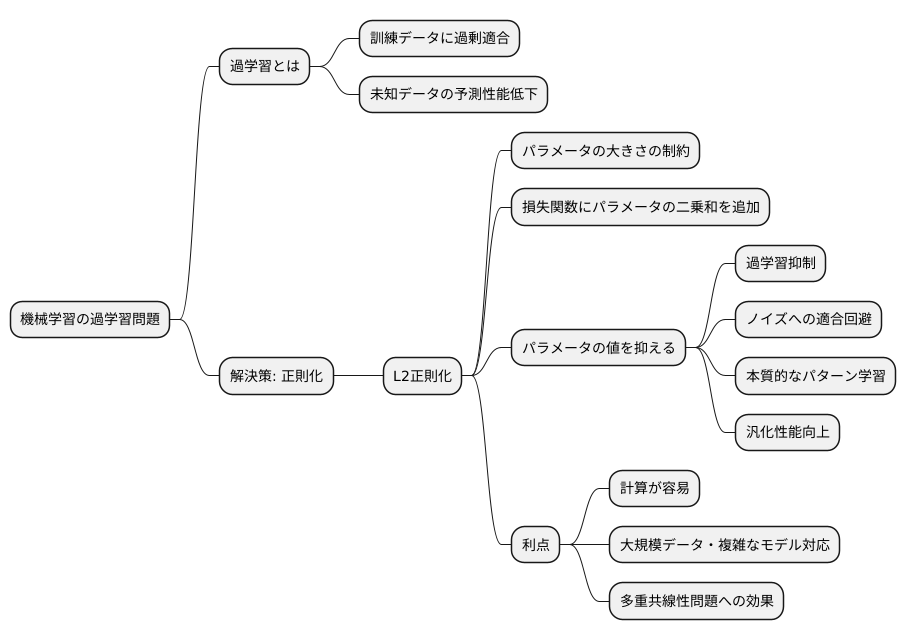
機械学習では、学習に使ったデータに対しては高い精度を示す一方で、新しいデータに対してはうまく予測できないという問題が起こることがあります。これは、まるで試験勉強で過去問だけを完璧に覚えてしまい、応用問題に対応できないような状態です。このような現象を過学習と呼びます。
この過学習を防ぐための有効な手段として、正則化という方法があります。正則化とは、モデルが複雑になりすぎるのを防ぎ、未知のデータに対しても安定した予測ができるようにする技術です。
具体的には、モデルの学習中に、損失関数と呼ばれる指標に正則化項を加えます。損失関数は、モデルの予測が実際の値からどれくらい離れているかを表す尺度で、この値を小さくすることが学習の目標です。正則化項は、モデルのパラメータの大きさにペナルティを科す役割を果たします。パラメータとは、モデルの特性を決める値のようなもので、この値が大きくなりすぎると、モデルが複雑になりすぎて過学習を起こしやすくなります。
例えるなら、複雑な数式をたくさん使って問題を解こうとするよりも、単純な数式で本質を捉えた方が、新しい問題にも対応しやすいのと同じです。正則化項を加えることで、パラメータの値が大きくなりすぎるのを抑え、モデルをより単純な形に保つことができます。
結果として、モデルは学習データの細かな特徴に囚われすぎることなく、データ全体の傾向を捉えることができるようになり、未知のデータに対してもより正確な予測を行うことが可能になります。正則化は、機械学習において汎化性能を高めるための重要な技術と言えるでしょう。
L2正則化の仕組み

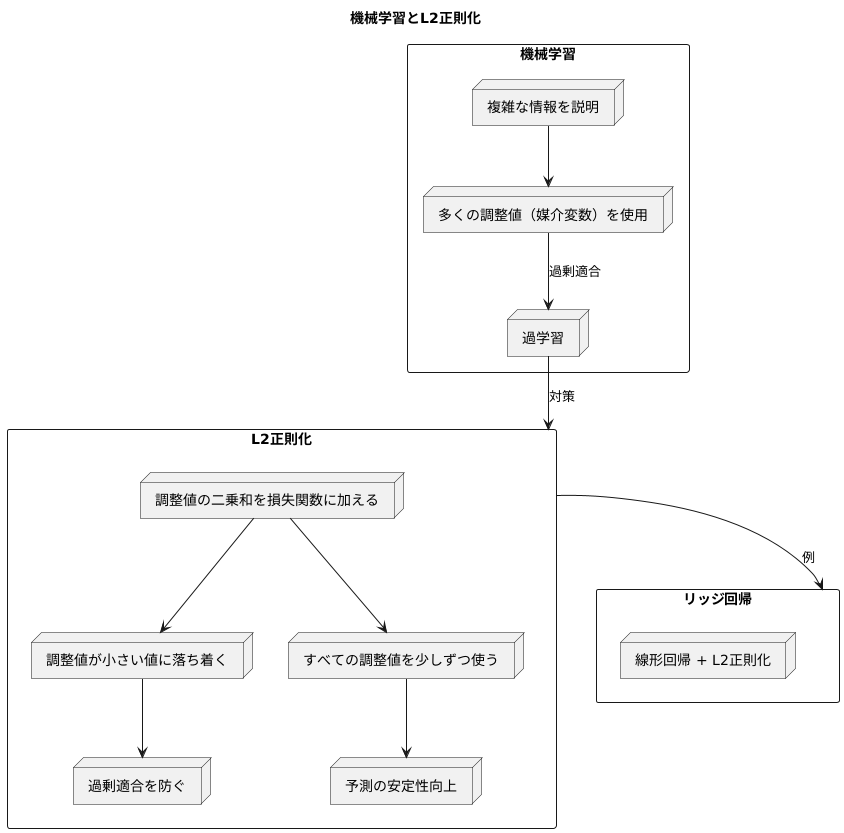
多くの学び取りをする機械学習の手法では、複雑な情報をうまく説明できるよう、たくさんの調整値(これを専門的には媒介変数と呼びます)を使います。しかし、あまりに調整値を細かく設定しすぎると、学習に用いた情報に過剰に適合してしまい、新しい情報に対してうまく対応できなくなることがあります。これは、いわば勉強のしすぎで応用が利かなくなる状態であり、過学習と呼ばれています。この過学習を防ぐための工夫の一つが正則化であり、L2正則化はその代表的な方法です。
L2正則化は、調整値の大きさの二乗をすべて足し合わせたもの(二乗和)を、本来の学習の目標である損失関数に加えることで実現されます。損失関数は、学習データとのずれを表す指標であり、この値を小さくすることが学習の目的です。ここに調整値の二乗和が加わることで、調整値が大きくなりすぎると損失関数も大きくなってしまうため、学習の過程で調整値は小さい値に落ち着こうとする性質を持ちます。
調整値が小さいということは、情報に対する反応が穏やかになることを意味し、結果として過剰適合を防ぐ効果につながります。例えば、線形回帰という基本的な予測手法にL2正則化を適用したものは、リッジ回帰と呼ばれ、広く活用されています。
L2正則化では、調整値の二乗和を用いるため、個々の調整値はゼロに近い値を取りやすくなります。しかし、完全にゼロになることはほとんどありません。これは、L2正則化がすべての調整値を少しずつ使うという特徴を持っているためです。まるで、料理に様々な香辛料を少しずつ加えることで、全体の味を調えるように、L2正則化は多くの情報を少しずつ考慮することで、予測の安定性を高めます。つまり、あまり重要でない情報の影響を弱めつつ、すべての情報を活用することで、より堅牢な予測モデルを構築することができるのです。
L1正則化との違い

機械学習において、過学習はモデルの精度を落とす大きな問題です。この過学習を防ぐための手法の一つとして、正則化があります。正則化には様々な種類がありますが、L1正則化とL2正則化は代表的な手法です。どちらもモデルのパラメータに制限を加えることで過学習を抑えますが、その働きには違いがあります。
L1正則化は、パラメータの絶対値の合計を正則化項として用います。このため、L1正則化は特定のパラメータを完全にゼロにする性質があります。不要なパラメータをゼロにすることで、モデルを単純化し、重要な特徴量だけを残す効果があります。これは特徴量選択と呼ばれ、データの解釈性を高めるのに役立ちます。結果として、必要な特徴量だけを使った簡潔なモデルが得られます。
一方、L2正則化は、パラメータの二乗の合計を正則化項として用います。L2正則化はパラメータをゼロに近づけますが、L1正則化のように完全にゼロにすることは稀です。つまり、全ての特徴量をモデルに含めたまま、影響の少ない特徴量の重みを小さくすることで、モデル全体のバランスを整えます。これは、多くの特徴量が複雑に絡み合っている場合に有効です。L2正則化によって、モデルの安定性が向上し、過学習が抑えられます。
このように、L1正則化とL2正則化はそれぞれ異なる特性を持っています。どちらの手法が適しているかは、扱うデータの性質やモデルの目的によります。データの中に重要度の低い特徴量が多数含まれている場合はL1正則化が、全ての特徴量が重要な役割を果たしている場合はL2正則化が適していることが多いです。それぞれの特性を理解し、適切に使い分けることが重要です。
| 項目 | L1正則化 | L2正則化 |
|---|---|---|
| 正則化項 | パラメータの絶対値の合計 | パラメータの二乗の合計 |
| パラメータへの影響 | 不要なパラメータをゼロにする | パラメータをゼロに近づける(完全にゼロにはなりにくい) |
| 効果 | 特徴量選択、モデルの簡潔化、データの解釈性向上 | モデルの安定性向上、過学習抑制 |
| 適している場合 | 重要度の低い特徴量が多数含まれている場合 | 全ての特徴量が重要な役割を果たしている場合 |
L2正則化の利点

機械学習では、訓練データに過剰に適合してしまう過学習という問題がよく起こります。過学習が起きると、訓練データに対する精度は高いものの、未知のデータに対する予測性能は低くなってしまいます。この問題を解決する有力な手法の一つが、正則化という技術です。その中でも、L2正則化は広く使われている手法です。
L2正則化は、モデルのパラメータの大きさに関する制約を導入することで、過学習を抑制します。具体的には、損失関数にパラメータの二乗和を加えることで、パラメータの値が大きくなりすぎるのを防ぎます。この仕組みにより、モデルは訓練データの細かいノイズにまで適合することを避け、本質的なパターンを学習するように促されます。結果として、未知のデータに対しても、より安定した予測ができるようになります。つまり、汎化性能が向上するのです。
L2正則化の大きな利点の一つは、計算が比較的容易であることです。これは、大規模なデータセットや複雑なモデルを扱う場合に特に重要です。計算コストを抑えることができるため、効率的に学習を進めることができます。
さらに、L2正則化は、多重共線性という問題にも効果があります。多重共線性とは、説明変数(特徴量)の間に強い相関がある状態を指します。このような状態では、モデルのパラメータの推定が不安定になり、予測性能が低下する可能性があります。L2正則化は、パラメータの値を小さく抑えることで、この不安定さを軽減し、より信頼性の高いモデルを構築することができます。このように、L2正則化は、様々な場面でモデルの性能向上に役立つ、強力なツールと言えるでしょう。
実践的な学習方法

物事を深く理解するには、本や教科書で学ぶだけでなく、実際に自分の手でやってみるという経験が欠かせません。特に、近年の技術発展が目覚ましい情報処理の分野では、理論と実践の両輪を回すことがより重要になります。たとえば、近年注目を集めている学習方法の正則化という手法。この正則化を学ぶための実践的な学習機会として、人気の学習動画配信者である「ヨビノリ」氏との共同企画が立ち上がりました。
この企画では、動画配信サイトと記事投稿サイトの両方を使って、正則化の中でも特に重要な二つの手法であるL1正則化とL2正則化について学ぶことができます。動画配信サイトでは、正則化とは何かという基本的な説明から、それぞれの正則化が持つ意味や効果について、図表などを用いて分かりやすく解説しています。難しい数式も、丁寧に紐解きながら説明してくれるので、安心して学ぶことができます。さらに、記事投稿サイトでは、プログラミング言語の一つであるPythonを使って、実際に正則化をどのように実現するのかを学ぶことができます。記事には具体的な手順がコードとともに掲載されているので、自分の手を動かしながら学ぶことができます。
この共同企画は、理論と実践の両面から正則化を学ぶことができる貴重な機会です。正則化は、情報処理の分野で近年ますます重要性を増している学習方法の一つであり、特に深層学習と呼ばれる分野では無くてはならない技術となっています。この企画を通して正則化を学ぶことで、深層学習をはじめとする様々な情報処理技術の理解を深めることができるでしょう。ぜひ、動画や記事を通して学習を進め、理解を深めてみてください。きっと、今後の学びや研究の大きな助けとなるはずです。
| 項目 | 内容 |
|---|---|
| テーマ | 正則化(L1正則化、L2正則化) |
| 学習方法 | 動画配信サイト、記事投稿サイト |
| 動画配信サイト | 正則化の基本説明、L1/L2正則化の意味・効果解説(図表使用)、数式の解説 |
| 記事投稿サイト | Pythonを使った正則化の実現方法、コード付き手順解説 |
| 講師 | ヨビノリ氏 |
| 対象分野 | 情報処理、深層学習 |
