自己回帰モデルで未来予測

AIを知りたい
『自己回帰モデル』って言葉が出てきたのですが、よく分かりません。教えて下さい。

AIエンジニア
そうですね。「自己回帰モデル」は、過去のデータを使って未来のデータを予測する手法です。例えば、昨日の気温から今日の気温を予測したり、過去の株価から今日の株価を予測したりするのに使われます。

AIを知りたい
過去のデータを使うというのは、なんとなく分かります。今日の気温は昨日の気温と関係ありそうですよね。でも、具体的にどうやって予測するのですか?

AIエンジニア
簡単に言うと、過去のデータに、ある計算式を当てはめて計算します。その計算式にはいくつか調整できる数字があって、予測がより正確になるように調整します。例えば、今日の気温を予測するために、昨日の気温に0.8をかける、といった計算式を使うとします。この0.8という数字を調整することで、より正確な予測ができるようにするのです。
自己回帰モデルとは。
人工知能で使われる言葉に「自己回帰モデル」というものがあります。これは、過去のデータを使って現在のデータを予測する手法で、株価や天気予報のように、時間の流れに沿って変化するデータの予測によく用いられます。例えば、ある時点での値を予測したい場合、その値は一つ前の時点での値と、その時点特有の偶然による変化、そして一定の値を足し合わせたものとして計算されます。この計算式に含まれる調整のための値は、最小二乗法や最尤法といった統計的な方法で見つけ出されます。
自己回帰モデルとは

自己回帰モデルとは、過去の情報を使って未来を予測する統計的手法です。過去のデータが、未来の出来事を予測するための重要な手がかりとなると考えるモデルです。まるで、過去の自分の行動や経験を振り返ることで、未来の自分の行動や起こる出来事を予測する、と言えるでしょう。
このモデルは、過去の情報が未来にも影響を与え続けると仮定しています。過去の出来事が現在の状況に影響を与え、現在の状況が未来の状況に影響を与える、という連鎖が続くのです。例えば、今日の気温が昨日の気温に影響を受け、明日の気温は今日の気温に影響を受ける、といった具合です。また、ある製品の今日の売上高が昨日の売上高に影響を受け、明日の売上高が今日の売上高に影響を受ける、といった例も考えられます。
この連鎖反応を数式で表すことで、未来の値を予測することができます。数式には、過去のデータがどれくらい未来の値に影響を与えるかを示す係数が含まれています。この係数は、過去のデータと未来のデータの関係性から計算されます。係数が大きければ大きいほど、過去のデータの影響が強いことを意味します。
自己回帰モデルは、株価や気温、売上高といった時間の流れとともに変化するデータの予測によく用いられます。過去のデータが未来を予測する重要な情報となるため、データの質と量は予測精度に大きな影響を与えます。過去のデータが多ければ多いほど、そしてデータの質が良ければ良いほど、未来予測の精度は高まる傾向にあります。過去の経験をたくさん積めば積むほど、未来の出来事を予測しやすくなるのと同じと言えるでしょう。ただし、未来を完璧に予測することは非常に難しいです。自己回帰モデルはあくまでも予測を行うための道具であり、予測結果が必ずしも現実と一致するとは限りません。
| 項目 | 説明 |
|---|---|
| 定義 | 過去の情報を使って未来を予測する統計的手法 |
| 仮定 | 過去の情報が未来にも影響を与え続ける |
| 例 | 気温、売上高、株価など |
| 数式 | 過去のデータの影響度を示す係数を含む |
| 予測精度 | データの質と量に依存 |
| 注意点 | 予測結果が必ずしも現実と一致するとは限らない |
モデルの仕組み

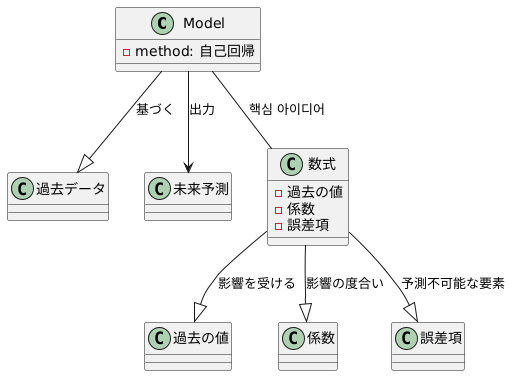
このモデルは、過去データに基づいて未来を予測する、自己回帰という方法を用いています。過去のデータと未来のデータの関係を数式で表すことが、このモデルの核となる考え方です。
未来のある時点の値を予測するには、その直前の時点の値だけでなく、もっと前の時点の値も必要になります。例えば、明日の気温を予測するには、今日の気温だけでなく、昨日の気温、一昨日の気温なども影響を与える可能性があります。このように、予測したい時点より前の複数の時点の値が、未来の値に影響を与えると考えます。
過去のそれぞれの時点の値が、未来の値にどの程度影響を与えるかは、係数という数値で表します。係数の値が大きいほど、過去のその時点の値の影響力が強いことを意味します。例えば、今日の気温が明日の気温に大きく影響するのであれば、今日の気温に対応する係数は大きな値になります。逆に、一昨日の気温は明日の気温にあまり影響を与えないのであれば、一昨日の気温に対応する係数は小さな値になります。
しかし、過去のデータから未来の値を完全に予測することはできません。予測できない偶然の出来事や、観測時の小さな誤差なども影響を与えるからです。このような予測できない要素は、誤差項という形で数式に組み込みます。誤差項は、周りの環境の変化や測定の誤差といった、予測に含めることが難しい要素を表すものです。
過去の値の影響を表す係数と、予測できない要素を表す誤差項、そして過去の値を組み合わせることで、未来の値を予測するための数式が完成します。この数式に過去のデータを当てはめることで、未来の値を計算することができるのです。
パラメータ推定

時系列データを分析し、将来の値を予測するために、自己回帰モデルをよく使います。このモデルの肝となるのがパラメータ推定です。パラメータとは、過去のデータがどれくらい未来の値に影響するかを示す数値のことです。適切なパラメータを見つけることで、モデルの予測精度が大きく向上します。
自己回帰モデルでは、過去のデータが未来の値に影響を与えると仮定します。例えば、今日の気温が昨日の気温に影響を受けるといった具合です。この影響の度合いを表すのがパラメータです。もし昨日の気温の影響が大きければ、パラメータの値は大きくなります。逆に影響が小さければ、パラメータの値は小さくなります。パラメータは過去のデータの影響度合いを示す重みのようなものと言えるでしょう。
このパラメータを推定する際に、よく用いられるのが最小二乗法と最尤法です。最小二乗法は、モデルの予測値と実際の値の差の二乗を合計したものを最小にするようにパラメータを調整します。予測値と実際の値の差が小さいほど、モデルの精度は高いと考えられます。この差を二乗するのは、正負の値を相殺させずに、差の大きさを適切に評価するためです。
一方、最尤法は、観測されたデータが得られる確率を最大にするようにパラメータを調整します。つまり、実際に得られたデータが最も出現しやすいようにパラメータを決める方法です。現実のデータに最もよく合うパラメータを見つけることで、将来の予測精度を高めることができます。
このように、最小二乗法と最尤法といった統計的な手法を用いることで、過去のデータに最も適合するパラメータを見つけることができます。そして、最適なパラメータを用いることで、自己回帰モデルは未来の値をより正確に予測できるようになるのです。
| 手法 | 説明 |
|---|---|
| 最小二乗法 | モデルの予測値と実際の値の差の二乗和を最小にすることでパラメータを推定。 |
| 最尤法 | 観測されたデータが得られる確率を最大にするようにパラメータを推定。 |
様々な応用事例

自己回帰モデルは、過去データに基づいて未来を予測する手法であり、様々な分野で活用され、私たちの暮らしを支えています。
金融の世界では、株価の動きを予測するために自己回帰モデルが利用されています。過去の株価の変動パターンを学習することで、将来の株価を予測し、より効果的な投資判断を行うことが可能になります。また、為替レートや金利の予測にも役立ち、市場リスクの管理に貢献しています。
天気予報においても、自己回帰モデルは重要な役割を果たしています。過去の気温や降水量、風速などの気象データを基に、将来の天気を予測することで、豪雨や台風などの自然災害への備えを促すことができます。日々の天気予報はもちろんのこと、長期的な気候変動の予測にも活用され、農業や防災など様々な分野で役立っています。
企業活動においては、需要予測に自己回帰モデルが活用されています。過去の売上データや市場トレンドを分析することで、将来の製品需要を予測し、最適な在庫量を決定することができます。過剰在庫による損失を減らすだけでなく、機会損失を防ぐことにも繋がり、企業経営の効率化に貢献しています。
さらに、私たちの身近な技術にも、自己回帰モデルは応用されています。音声認識では、過去の音声データから音声を認識する精度を高め、より自然な音声対話システムの実現に貢献しています。また、画像認識では、画像内の物体を認識する精度を向上させ、自動運転技術や医療画像診断など、様々な分野で革新的な技術開発を支えています。このように自己回帰モデルは、様々な分野で未来予測のための重要な道具として活用され、私たちの生活をより便利で豊かなものにしています。
| 分野 | 活用例 | 効果 |
|---|---|---|
| 金融 | 株価、為替レート、金利の予測 | 効果的な投資判断、市場リスクの管理 |
| 天気予報 | 短期・長期の天気予報、気候変動予測 | 自然災害への備え、農業・防災への貢献 |
| 企業活動 | 需要予測 | 在庫最適化、損失削減、経営効率化 |
| 音声認識 | 音声認識精度の向上 | 自然な音声対話システムの実現 |
| 画像認識 | 画像認識精度の向上 | 自動運転、医療画像診断などへの貢献 |
モデルの限界

自己回帰モデルは、過去のデータから未来を予測する強力な道具です。まるで過去の出来事が未来の鏡のように、過去のデータが未来を映し出すと仮定して計算を行います。しかし、このモデルにはいくつかの限界があります。
まず、自己回帰モデルは、物事が急に変わったり、予想外の出来事が起こったりするとうまく機能しません。過去のデータが未来にも同じように影響を与え続けると考えているため、経済の大きな落ち込みや自然災害といった、過去のデータには含まれていないような出来事の影響をうまく捉えることができません。例えば、過去の景気の推移から未来の景気を予測する場合、突然の感染症の流行による経済への影響は予測できないでしょう。
また、長い期間の予測は難しいという問題もあります。予測する期間が長くなるほど、予測の精度は落ちていきます。天気予報で例えると、明日の天気は高い確率で当たるかもしれませんが、一週間後の天気の精度は下がってしまうのと同じです。
さらに、モデルが複雑になると計算に時間がかかってしまうこともあります。複雑な計算をするには多くの資源が必要になり、結果を得るまでに時間がかかります。
これらの限界を理解した上で、自己回帰モデルを使うことが大切です。自己回帰モデルによる未来予測は、あくまで予測であり、必ず当たるという保証はありません。未来を完璧に予測することは不可能です。予測結果を参考にしながら、周りの状況をよく見て、必要に応じて対応を変える柔軟さを持つことが重要です。まるで航海士が羅針盤を頼りにしながらも、波や風の様子を見て航路を調整するように、予測結果を一つの指針として、現実の変化に対応していくことが重要です。
| メリット | デメリット |
|---|---|
| 過去のデータから未来を予測できる強力な道具 | 急な変化や予想外の出来事に対応できない 例:感染症流行による経済への影響は予測できない |
| 長期予測の精度は低い 例:天気予報は明日より1週間後の方が精度は低い |
|
| モデルが複雑になると計算に時間がかかる |
今後の展望

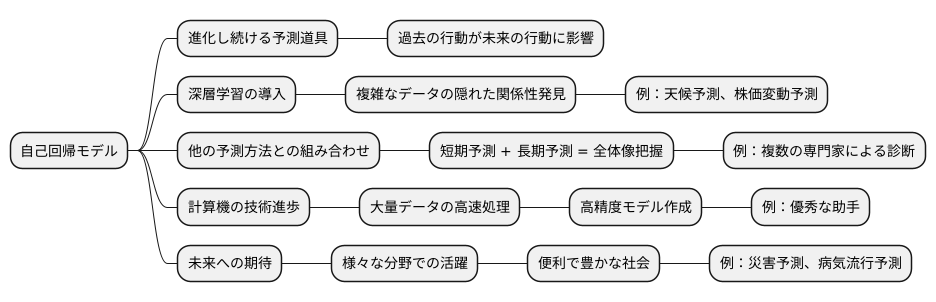
自己回帰という考え方は、過去の自分の行動が未来の自分の行動に影響を与えるという考え方で、予測を行うための大切な道具です。この道具は、常に改良が加えられ進化し続けています。近年では、人間の脳の仕組みを真似た「深層学習」という技術を取り入れた自己回帰の研究開発が盛んに行われており、これまで以上に正確な予測ができるようになりつつあります。
深層学習を使うことで、複雑なデータに隠された、単純な比例関係ではない、入り組んだ関係性を見つけ出すことができます。これにより、従来の自己回帰の手法では難しかった予測も可能になります。例えば、天候の予測や株価の変動予測など、複雑な要素が絡み合う事象についても、より精度の高い予測が可能になるでしょう。
また、他の予測方法との組み合わせも研究されています。それぞれの予測方法の得意な部分を活かすことで、より精度の高い予測手法が開発されています。例えば、自己回帰モデルで短期的な変動を予測し、別のモデルで長期的な傾向を予測することで、より全体像を捉えた予測が可能になります。これは、まるで複数の専門家がそれぞれの知識を持ち寄り、より正確な診断を行うようなものです。
さらに、たくさんのデータを速く処理できる計算機の技術の進歩も、自己回帰モデルの発展を後押ししています。大量のデータを使って学習させることで、より精度の高いモデルを作ることが可能になります。この進歩は、まるで優秀な助手が膨大な資料を整理し、必要な情報をすぐに提供してくれるようなものです。
自己回帰モデルは、未来を予測するための大切な道具として、今後も進化し続け、様々な分野で活躍していくことが期待されます。より高度な予測技術の開発により、私たちの社会はもっと便利で豊かなものになっていくでしょう。例えば、災害の発生を予測して被害を減らしたり、病気の流行を予測して対策を立てたり、様々な場面で役立つことが期待されます。