方策勾配法:直接最適な方策を見つける学習

AIを知りたい
先生、「方策勾配法」がよくわからないです。Q学習のように価値を計算していく方法と何が違うんですか?

AIエンジニア
いい質問だね。Q学習は、それぞれの行動の価値を計算して、一番価値の高い行動を選ぶ方法だったよね。方策勾配法は、価値を計算する代わりに、直接行動の選び方を学習していく方法なんだ。

AIを知りたい
行動の選び方を直接学習する? どういうことですか?

AIエンジニア
例えば、ロボットにサッカーをさせたいとしよう。Q学習だと、ドリブル、パス、シュートなど、それぞれの行動の価値を計算する必要がある。でも、方策勾配法では、状況に応じて、どの行動をどれくらいの確率で選ぶか、というのを直接学習するんだ。行動の種類が多い時ほど、価値を計算するのは大変だから、方策勾配法の方が良い場合もあるんだよ。
方策勾配法とは。
人工知能の用語で『方策勾配法』というものがあります。最適な行動方針を見つけるのは難しいので、Q学習といった方法は、行動の良し悪しを評価する関数をより良くしていくという考え方を使っています。一方、方策勾配法は、直接最適な行動方針を見つけ出すという方法です。この方法では、行動方針をいくつかの数値で表される関数とみなし、その数値を学習することで、行動方針自体を学習します。この方法は特に、行動の選択肢が多い場合に使われます。行動の選択肢が多いと、それぞれの行動の良し悪しを計算するのに莫大な費用がかかり、学習が不可能になってしまうからです。
方策勾配法とは

方策勾配法は、賢い機械を作るための学習方法である強化学習における、機械の行動指針を直接学習する画期的な手法です。
従来の強化学習では、まずそれぞれの状況における行動の良し悪しを評価する指標を学習し、その指標に基づいて最も良い行動を選びます。例えば、迷路を解くロボットの場合、従来の手法では、迷路の各地点で、上下左右に動くことの価値を数値で評価する表のようなものをまず作ります。そして、その表に基づいて、最も価値の高い方向へと移動します。
一方、方策勾配法は、このような良し悪しを評価する指標を介さずに、行動指針そのものを直接学習します。これは、迷路の例でいうと、各地点でどの方向に動くかの確率を直接調整するようなイメージです。この行動指針は、数値で表現できる関数で表され、その関数の微調整を繰り返すことで、最適な行動指針を見つけ出します。
この直接的な学習方法は、特に複雑な問題や行動の種類が多い場合に威力を発揮します。例えば、囲碁や将棋のようなゲームでは、可能な行動の数が膨大であるため、従来の方法ではすべての行動の良し悪しを評価するのに膨大な時間がかかります。しかし、方策勾配法では、行動指針を直接学習するため、このような計算の負担を軽減し、効率的な学習を実現できます。また、良し悪しを評価する指標を経由しないため、より複雑で柔軟な行動指針を学習できるという利点もあります。つまり、従来の方法では表現が難しかった、状況に応じた微妙なさじ加減を学習できる可能性を秘めているのです。
| 項目 | 従来の強化学習 | 方策勾配法 |
|---|---|---|
| 学習対象 | 行動の良し悪しを評価する指標(例:迷路の各地点での上下左右の価値) | 行動指針そのもの(例:迷路の各地点でどの方向に動くかの確率) |
| 学習方法 | 指標に基づいて、最も良い行動を選択 | 行動指針を直接学習(関数の微調整) |
| 複雑な問題への対応 | 行動の種類が多い場合、計算コスト大 | 効率的な学習が可能 |
| 利点 | – | 複雑で柔軟な行動指針を学習可能、状況に応じた微妙なさじ加減を学習できる可能性 |
| 例 | 迷路ロボット、囲碁、将棋 | 迷路ロボット、囲碁、将棋 |
価値関数との違い

「価値関数」を利用した手法と「方策勾配法」の大きな違いは、行動の選び方にあります。
価値関数に基づく手法、例えば「Q学習」では、まず各状態と各行動の組み合わせに対する価値を数値で示す「価値関数」を学習します。
たとえば、迷路の例で考えると、各地点(状態)で、上下左右に動く(行動)という組み合わせそれぞれに、ゴールまでの道のりの良さ(価値)を数値で表します。
そして、価値が最も高い行動、つまりゴールへの近道だと判断した行動を選びます。
この方法は、迷路のような状態の種類や行動の種類が少ない場合にはうまくいきます。しかし、状態や行動の種類が非常に多い複雑な問題では、すべての状態と行動の組み合わせを計算するのに、膨大な時間がかかります。
例えば、囲碁のように盤面の状態や打てる場所が多岐にわたる場合、すべての状態と行動の価値を計算するのは現実的ではありません。
一方、方策勾配法は、価値関数を経由せずに、直接行動の選び方を学習します。
迷路の例で言えば、各地点で上下左右どの行動をとるかの確率を直接学習します。
価値関数を学習する必要がないため、状態や行動の種類が多い場合でも、効率的に学習を進めることができます。
囲碁のように複雑な問題でも、方策勾配法は有効な手段となります。
このように、方策勾配法は価値関数を用いる手法とは学習のアプローチが根本的に異なり、状態や行動の種類が多い問題に適しています。
| 手法 | 行動の選び方 | メリット | デメリット | 例 |
|---|---|---|---|---|
| 価値関数に基づく手法 (e.g., Q学習) | 各状態と行動の組み合わせに対する価値(価値関数)を学習し、価値が最も高い行動を選ぶ | 状態や行動の種類が少ない場合に有効 | 状態や行動の種類が多い場合、計算に膨大な時間がかかる | 迷路 |
| 方策勾配法 | 価値関数を経由せずに、直接行動の選び方を学習 (e.g., 各地点で上下左右どの行動をとるかの確率を直接学習) | 状態や行動の種類が多い場合でも効率的に学習できる | – | 囲碁 |
パラメータによる方策表現

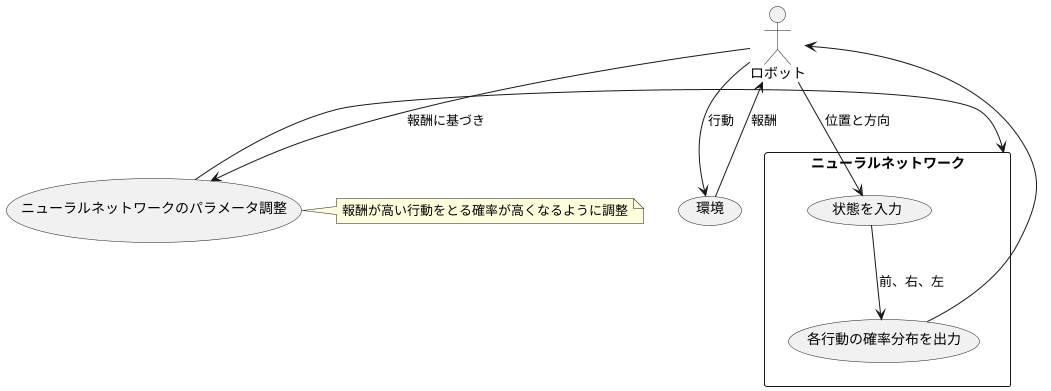
方策勾配法は、方策を調整可能な数値(パラメータ)を使って表した関数で表現します。この関数は、ある状態に対してどのような行動をとるべきかを確率分布の形で出力します。たとえば、迷路にいるロボットの位置と方向が「状態」だとすると、この「状態」を入力として、ロボットが次に「前へ進む」「右へ曲がる」「左へ曲がる」といった行動をとる確率を計算するのが、パラメータで表された方策の役割です。
この方策を表す関数として、ニューラルネットワークがよく使われます。ニューラルネットワークは、人間の脳の神経細胞の繋がりを模倣した数理モデルで、入力された情報に基づいて計算を行い、結果を出力します。方策勾配法では、ニューラルネットワークの入力に「状態」を、出力に各行動の確率分布を設定します。例えば、迷路のロボットの場合、ロボットの位置と方向といった「状態」がニューラルネットワークに入力され、各方向に進む確率が出力されます。
学習は、試行錯誤を通して行われます。ロボットが迷路の中で行動し、ゴールにたどり着けば報酬が与えられます。この報酬に基づいて、ニューラルネットワークのパラメータ(重みやバイアスと呼ばれる数値)を調整します。具体的には、報酬が高い行動をとる確率が高くなるようにパラメータを更新します。例えば、右に曲がったら報酬が大きかった場合、次に同じような状態になったら右に曲がる確率が大きくなるように、ニューラルネットワークのパラメータを調整します。
このように、試行錯誤とパラメータの調整を繰り返すことで、ニューラルネットワークはより良い行動を選択するよう学習していきます。最終的には、どのような状態でも最適な行動をとる確率が最も高くなるように、ニューラルネットワークのパラメータが調整され、最適な方策を獲得します。つまり、迷路のロボットであれば、最短経路でゴールにたどり着く確率が最も高くなる方策を学習することになります。
行動の種類が多い場合の利点

多くの行動から最適なものを選ぶ必要がある複雑な状況を考えてみましょう。例えば、ロボットアームが様々な物体をつかむ作業や、自動運転車が複雑な交通状況で適切な運転操作を選択する場面などが挙げられます。このような状況では、行動の種類が多いほど、より細かい制御や柔軟な対応が可能になります。しかし、膨大な選択肢の中から最適な行動を見つけることは容易ではありません。
従来の、行動の価値を評価に基づいて選択する手法では、行動の種類が増えるほど、それぞれの価値を計算するのに時間がかかり、学習の効率が低下します。特に、ロボットの関節角度のように連続的な値を取る行動の場合、行動の種類は無限に存在するため、従来の手法では対応できません。
これに対し、方策勾配法と呼ばれる手法は、行動を選択する方策そのものを学習します。この方策は、状況に応じてどの行動をとるべきかを確率的に決定する関数で表現されます。方策は少数の調整可能な数値(パラメータ)によって制御され、パラメータを調整することで、最適な行動を直接探索できます。
方策勾配法の利点は、連続的な行動空間にも対応できる点です。例えば、ロボットアームの関節角度を連続的に変化させる場合でも、方策のパラメータを調整することで、滑らかな動きを実現できます。また、方策を確率的に表現することで、探索と活用のバランスを取ることができます。つまり、既知の最適な行動だけでなく、未知の行動も試すことで、より良い行動を見つける可能性を高めます。
このように、方策勾配法は行動の種類が多い場合に特に有効であり、複雑な問題を解くための強力な手法として注目されています。
| 手法 | 説明 | 長所 | 短所 | 適用可能 |
|---|---|---|---|---|
| 従来手法(価値ベース) | 行動の価値を評価に基づいて選択 | – | 行動の種類が多いと計算コスト大、学習効率低下 連続値の行動空間には対応不可 |
行動の種類が少ない場合 |
| 方策勾配法 | 状況に応じて行動を選択する方策そのものを学習 方策は確率的に行動を決定する関数で表現 少数の調整可能なパラメータで制御 |
連続値の行動空間にも対応可能 探索と活用のバランスを取れる 複雑な問題を解くことが可能 |
– | 行動の種類が多い場合、連続値の行動空間 |
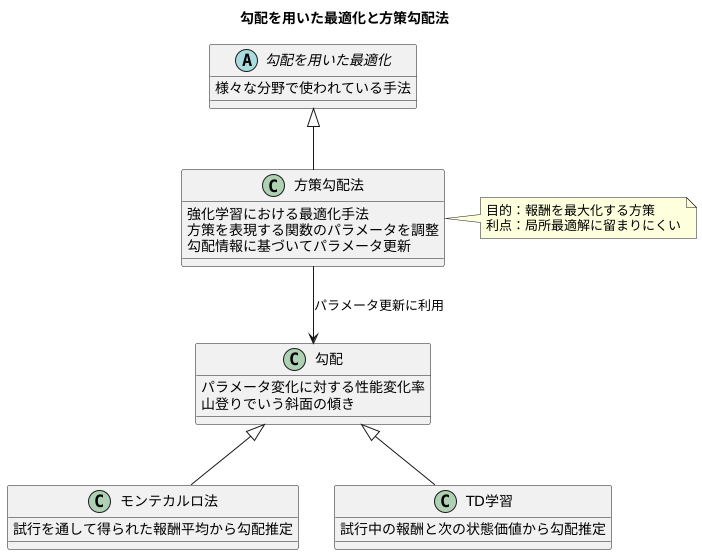
勾配を用いた最適化

勾配を用いた最適化は、様々な分野で広く使われている手法であり、方策勾配法もその応用の一つです。方策勾配法とは、強化学習において、方策を表現する関数のパラメータを調整することで、エージェントの行動を最適化する手法です。この最適化は、勾配と呼ばれる概念を基に行われます。勾配とは、パラメータを少しだけ変化させた際に、方策の性能がどれほど変化するかを示す指標です。具体的には、パラメータ空間における方策の性能の変化率をベクトルで表したものが勾配です。
方策勾配法では、この勾配情報を用いて、方策の性能、つまり得られる報酬が大きくなる方向にパラメータを調整していきます。山登りに例えると、勾配は山の斜面の傾きを表し、勾配が正の方向はより高い場所への方向を示しています。方策勾配法は、この山の斜面を登るように、勾配に従ってパラメータを更新することで、報酬を最大化する方策を探し出すのです。
勾配の推定には、モンテカルロ法やTD学習といった手法が用いられます。モンテカルロ法は、試行を通して得られた報酬の平均値から勾配を推定する方法です。一方、TD学習は、試行の途中で得られた報酬と次の状態の価値を使って勾配を推定する方法です。どちらの手法も、試行錯誤を通じて得られた情報から勾配を推定し、その推定値に基づいて方策を改善していくという考え方に基づいています。このように、勾配を用いた最適化は、試行錯誤を通して最適な行動を学習する強化学習において、非常に重要な役割を果たしているのです。また、勾配に基づいた最適化は、局所的な最適解に留まりにくく、より良い解、つまりより高い報酬を得られる方策を見つけ出す可能性を高めるという利点も持っています。
将来の発展

方策勾配法は、機械学習の中でも特に注目されている強化学習において、中心的な役割を担う学習方法です。これは、試行錯誤を通じて最適な行動方針を学習する方法であり、あたかも生き物が環境に適応していく過程を模倣しているかのようです。現在、この方策勾配法は活発に研究開発が進んでおり、将来、様々な分野で革新をもたらすことが期待されています。
特に近年、深層学習と呼ばれる技術と組み合わせた深層強化学習は目覚ましい成果を上げています。深層学習は、人間の脳の神経回路を模した仕組みで、大量のデータから複雑なパターンを学習することができます。この深層学習と方策勾配法を組み合わせることで、画像認識や自然言語処理といった分野で、従来の方法では難しかった高度なタスクをこなせるようになりました。例えば、画像を見て状況を判断し、適切な行動をとる、あるいは人間の話し言葉を理解し、自然な受け答えをするといったことが可能になっています。
今後、コンピュータの計算能力が向上し、より効率的な学習方法が見つかることで、方策勾配法はさらに複雑な問題にも対応できるようになると考えられます。例えば、ロボットの制御や自動運転技術への応用が期待されています。ロボットが複雑な環境でもスムーズに動き、人間の指示を理解して作業を行う、あるいは車が安全かつ効率的に目的地まで走行するといったことが実現可能になるでしょう。また、ゲームの人工知能も、より高度な戦略や戦術を学習し、人間に匹敵、あるいは凌駕するほどの能力を持つようになるかもしれません。
さらに、方策勾配法の理論的な研究も進められています。学習の仕組みをより深く理解することで、効率的な学習方法の開発や、学習過程の安定性の向上が期待されます。これにより、より少ない試行錯誤で、より確実に最適な行動方針を学習できるようになるでしょう。このように、方策勾配法は将来、人工知能の発展に大きく貢献し、私たちの生活をより豊かにしてくれると期待されています。
| 項目 | 説明 |
|---|---|
| 方策勾配法 | 強化学習の中心的な学習方法。試行錯誤を通じて最適な行動方針を学習。 |
| 深層強化学習 | 深層学習と方策勾配法の組み合わせ。画像認識や自然言語処理で高度なタスクを可能にする。 |
| 将来の応用 | ロボット制御、自動運転、ゲームAIなど。 |
| 理論的研究 | 学習の効率化、安定性の向上。 |
