主成分分析:データの次元を減らす

AIを知りたい
先生、主成分分析って難しそうだけど、簡単に言うとどんなものですか?

AIエンジニア
そうだね、たくさんの情報が詰まったデータから、重要な情報だけを抜き出して、もっと見やすくする技術だよ。 例えば、色んな果物の特徴(甘さ、色、大きさなど)を全部記録すると、データが複雑になるよね。 そこで、主成分分析を使うと、重要な特徴だけをまとめて、果物を少ない情報で区別しやすくできるんだ。

AIを知りたい
なるほど!でも、重要な情報だけを抜き出すと、何か情報がなくなったりしないんですか?

AIエンジニア
良い質問だね。確かに、細かい情報は少し失われてしまう。でも、全体的な特徴を捉えるには十分な情報が残るように抜き出すんだ。 例えば、果物の種類を見分けるのに、細かい傷の情報はあまり重要じゃないよね?そういう細かい情報を省くことで、全体像が見えやすくなるんだ。
PCAとは。
「人工知能に関係する言葉である『主成分分析』について説明します。主成分分析とは、たくさんの情報を持つデータを、より少ない情報で表す方法のことです。データの情報がたくさんあると、データの分析や機械学習で計算に時間がかかったり、データの全体像が分かりにくくなったりします。この問題を解決するために、統計学や機械学習の分野で主成分分析がよく使われています。主成分分析では、データの特徴を抜き出すことで、データの情報量を減らすことができます。情報量を減らして、三次元以下のデータにできれば、グラフなどでデータの様子を目に見えるようにすることもできます。主成分分析は、データの特徴をそのまま選ぶのではなく、新しい特徴を作り出すところがポイントです。ただし、この新しい特徴を作り出す操作は、元に戻すことができません。そのため、多少の情報が失われてしまうことを理解しておく必要があります。主成分分析は、情報量を減らすことを目的として、統計学だけでなく、生物学や生物情報科学など、様々な分野で使われています。
主成分分析とは

主成分分析とは、たくさんの性質を持つデータのもつ性質の数を減らす方法です。たくさんの性質を持つデータを、少ない性質で表すことで、データをとらえやすくするのが目的です。たとえば、100人の身長、体重、視力、足の大きさ、握力などのたくさんの情報があるとします。これらの情報をすべて使って分析するのは大変です。主成分分析を使うと、これらの情報を例えば「体格」と「運動能力」といった少数の性質にまとめることができます。
主成分分析は、データをより少ない性質で表現することで、データの全体像を把握しやすくします。高次元データ、つまりたくさんの性質を持つデータは、分析が難しく、全体像の把握も困難です。主成分分析によって次元数を減らす、つまり性質の数を減らすことで、データの可視化や解釈が容易になります。たくさんの情報に埋もれていたデータの構造や傾向が見えてくるのです。
主成分分析は、機械学習の分野でも広く使われています。機械学習では、大量のデータから学習を行うことがよくあります。しかし、データの性質が多すぎると、学習に時間がかかったり、うまく学習できなかったりすることがあります。主成分分析で性質の数を減らすことで、学習の効率を上げ、精度の向上を期待できます。
主成分分析は、情報の損失を最小限に抑えながら次元数を減らします。複雑な絵を単純な線画に変換するようなものです。線画には色の情報などは含まれませんが、絵の主要な特徴は捉えられています。同様に、主成分分析も、すべての情報を保持するわけではありませんが、データの最も重要な情報を残すように設計されています。
このように、主成分分析は、データ分析や機械学習において重要な役割を果たす手法です。大量のデータから本質を見抜き、効率的な分析や学習を実現するために、広く活用されています。
| 項目 | 説明 |
|---|---|
| 定義 | 多数の性質を持つデータの性質の数を減らす方法 |
| 目的 | 少ない性質でデータを表すことで、データをとらえやすくする |
| 例 | 100人の身長、体重、視力、足の大きさ、握力などの情報を「体格」と「運動能力」といった少数の性質にまとめる |
| メリット1 | データの全体像を把握しやすくする(高次元データの可視化や解釈を容易にする) |
| メリット2 | 機械学習の効率を上げ、精度の向上を期待できる |
| 特徴 | 情報の損失を最小限に抑えながら次元数を減らす(複雑な絵を単純な線画に変換するようなもの) |
特徴量の抽出

主成分分析(略して主成分分析)は、たくさんの数値データが持つ情報をなるべく損なわずに、少ない指標にまとめるための手法です。これは、データの持つ特徴をそのまま選ぶ特徴選択とは大きく異なります。特徴選択は、元々ある特徴の中からいくつかを選び出すだけですが、主成分分析は元のデータを使って全く新しい特徴を作り出します。この新しい特徴を主成分と呼びます。
主成分分析では、データ全体に広がる数値のばらつき具合に着目します。データのばらつきが大きい方向は、データの性質をよく表していると考えることができます。例えば、多くの人の身長と体重のデータがあるとします。身長も体重も個人差がありますが、もし身長が高い人ほど体重も重い傾向が強ければ、身長と体重のデータは同じような方向にばらついていると言えるでしょう。このばらつきの方向が主成分分析で重要な役割を果たします。
主成分は、データのばらつきが最も大きい方向に沿って作られます。最初の主成分は、データ全体のばらつきが最も大きい方向を示します。2番目の主成分は、最初の主成分と直交する方向の中で、ばらつきが最も大きい方向を示します。3番目以降の主成分も同様に、それ以前の主成分と全て直交する方向の中で、ばらつきが最も大きい方向を示します。このようにして作られた主成分は、元のデータの持つ情報をできるだけ多く保持するように設計されています。
主成分分析によって抽出された新しい特徴を使うことで、データの次元を削減し、処理を効率化することができます。また、ノイズ(不要な情報)の影響を減らし、データの本質的な特徴を捉えやすくなります。このため、主成分分析は、画像認識や音声認識、データマイニングなど、様々な分野で広く活用されています。重要なのは、主成分分析は単なる特徴の選択ではなく、元のデータから新しい特徴を抽出する手法であるということです。
次元削減と可視化

たくさんの情報を持つデータは、そのままでは全体像を掴むのが難しい場合があります。 例えば、数百もの項目からなるアンケート調査結果を想像してみてください。一つ一つの回答を細かく見ることはできますが、全体としてどのような傾向があるのかを理解するのは容易ではありません。このような場合に役立つのが、次元削減という手法です。次元削減は、データをより少ない情報量で表現する方法です。
次元削減の代表的な方法の一つに、主成分分析と呼ばれる手法があります。主成分分析は、データを最もよく表す特徴を見つけ出し、その特徴に基づいてデータをより少ない次元に変換します。元のデータが持つ多くの情報を、少数の主要な情報にまとめることで、データ全体の傾向を掴みやすくなります。
次元削減の大きな利点の一つは、データを視覚的に表現できるようになることです。人間は、3次元までの情報を視覚的に理解することができます。4次元以上のデータは、そのままでは図に表すことができません。しかし、次元削減によって3次元以下にまでデータの次元を減らすことができれば、散布図やグラフなどを用いてデータを視覚的に表現できます。
例えば、先ほどのアンケート調査結果を次元削減し、2次元にまで減らすことができたとします。そうすると、回答者の分布を平面上にプロットすることができます。似たような回答をした人たちは近くに集まり、異なる回答をした人たちは離れて分布する様子が視覚的に確認できます。これにより、データの中に隠れていた集団構造やデータのばらつきなどを容易に発見することが可能になります。このように、次元削減と可視化は、複雑なデータを理解するための強力な道具となります。
情報の損失

主成分分析(PCA)は、大量の情報をより少ない軸(主成分)で表現するための手法です。この手法は、データの持つ様々な特徴を、より少ない数の新しい特徴に集約することで、データの解釈や処理を容易にします。しかし、この集約の過程で、どうしても情報の一部が失われてしまうという欠点があります。
PCAは、データのばらつきの大きい方向に新しい軸を設定します。データのばらつきが大きい方向は、データの持つ情報を多く反映していると考えられるからです。言い換えれば、データの変化が大きい方向ほど、重要な情報を持っていると判断されます。そして、その軸にデータを射影することで、次元を削減します。
しかし、ばらつきの小さい方向にも、データの情報は含まれています。PCAでは、ばらつきの小さい方向の情報は重要でないと見なされ、切り捨てられてしまうのです。これが、情報が失われる主な原因です。
例えば、10個の特徴を持つデータがあるとします。PCAを用いて、このデータを3つの主成分で表現するとします。この場合、元の10個の特徴が持つすべての情報は、3つの主成分に完全に保存されるわけではありません。主成分は、元のデータのばらつきの大きな方向を主に捉えているため、ばらつきの小さな方向にあった情報は失われてしまいます。
情報の損失量は、PCAで設定する主成分の数に大きく影響されます。主成分の数を少なくすればするほど、次元削減の効果は高まりますが、同時に情報の損失量も増加します。逆に、主成分の数を多くすれば、情報の損失は少なくなりますが、次元削減の効果は薄れます。
そのため、PCAを利用する際には、情報の損失と計算コストの削減のバランスを考える必要があります。どの程度の情報の損失を許容できるのか、どの程度計算コストを削減したいのかを考慮し、適切な主成分の数を見つけることが重要です。これは、データの性質や分析の目的に応じて判断する必要があります。
| 項目 | 内容 |
|---|---|
| 主成分分析(PCA)とは | 大量の情報をより少ない軸(主成分)で表現するための手法。データの様々な特徴をより少ない新特徴に集約し、データの解釈や処理を容易にする。 |
| PCAの原理 | データのばらつきの大きい方向に新しい軸を設定。ばらつきの大きい方向はデータの情報が多く反映されていると考えるため。データの変化が大きい方向ほど重要な情報を持つと判断し、その軸にデータを射影することで次元を削減。 |
| PCAの欠点 | 情報の損失。ばらつきの小さい方向の情報は重要でないと見なされ切り捨てられる。 |
| 情報の損失 | 主成分の数に影響。主成分数を少なくすれば次元削減効果は高いが情報の損失量も増加。多くすれば情報の損失は少ないが次元削減効果は低い。 |
| PCA利用時の注意点 | 情報の損失と計算コスト削減のバランスを考慮。データの性質や分析の目的に応じて適切な主成分数を見つける。 |
様々な分野での応用

主成分分析(PCA)は、多くの分野で役立つ手法です。統計学はもちろんのこと、生物学や生物情報科学といった分野でも広く使われています。
例えば、遺伝子の働き具合を調べる遺伝子発現データの分析では、PCAは大きな力を発揮します。遺伝子発現データは、非常に多くの情報を含んでいるため、そのままでは解析が難しい場合があります。PCAを使うことで、データの持つ重要な特徴を保ちつつ、情報の量を減らすことができます。これにより、データの見通しが良くなり、解析がしやすくなります。たくさんの遺伝子の中から、特に重要な働きをする遺伝子を見つけ出すのに役立ちます。
画像認識の分野でも、PCAは活用されています。画像データは、そのままでは情報量が膨大で、処理に時間がかかります。PCAを用いて、画像データの特徴をうまく捉えたより少ない情報に変換することで、処理速度を上げることができます。また、ノイズと呼ばれる不要な情報を取り除く効果もあるため、画像認識の精度向上にも繋がります。例えば、手書きの文字を認識するシステムや、顔認証システムなどで、PCAが利用されています。
異常検知の分野でも、PCAは重要な役割を担っています。PCAを用いることで、普段とは異なるデータ、つまり異常なデータを簡単に見つけることができます。例えば、工場の機械の稼働状況を監視しているセンサーデータから、故障の前兆となる異常な値を検出するのに役立ちます。クレジットカードの不正利用の検知にも、PCAが応用されています。普段とは異なる使い方を素早く見つけることで、被害を最小限に抑えることができます。
このように、PCAは様々な分野で、データの解析を容易にし、新たな発見を導き出すための、強力な手法として利用されています。
| 分野 | PCAの役割 | 具体例 |
|---|---|---|
| 遺伝子発現データ分析 | 情報の量を減らし、データの見通しを良くする | 重要な遺伝子の発見 |
| 画像認識 | 処理速度向上、ノイズ除去、精度向上 | 手書き文字認識、顔認証 |
| 異常検知 | 異常なデータを簡単に見つける | 機械の故障予兆検知、クレジットカード不正利用検知 |
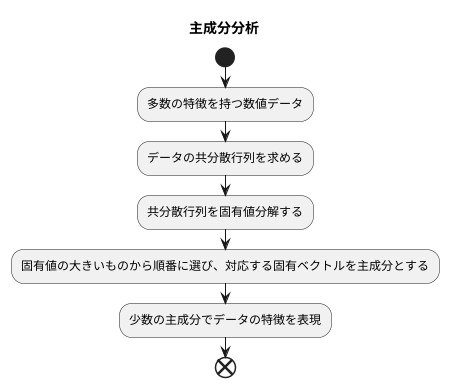
計算方法

主成分分析(略して主成分分析)は、たくさんの数値データが持つたくさんの特徴を、より少ない数の特徴でなるべくよく表すための計算方法です。たくさんの特徴をそのまま扱うのは大変なので、情報をなるべく失わずに整理して、計算を楽にするのが目的です。
この計算は、まずデータの共分散行列を求めることから始まります。共分散行列とは、それぞれの数値データの特徴同士がどれくらい関係しているかを示す表のようなものです。例えば、あるデータで身長と体重の特徴があった場合、身長が高い人は体重も重い傾向があるなど、特徴同士の関係の強さをこの表は示します。
次に、この共分散行列を固有値分解します。固有値分解とは、行列を分解して、固有値と固有ベクトルを求める計算のことです。固有ベクトルは、データの散らばり具合を最もよく表す方向を示すものです。イメージとしては、データの散らばりを雲のように考えた時、その雲が一番大きく広がっている方向を示す矢印のようなものです。そして、固有値は、それぞれの固有ベクトルがどれくらい重要かを示す数値です。雲の広がりで例えると、固有値が大きいほど、その方向に雲が大きく広がっていることを意味します。
主成分分析では、この固有値の大きいものから順番に選び、対応する固有ベクトルを主成分とします。固有値が大きいほど、その主成分がデータ全体の散らばりをより良く説明できるからです。
例えば、身長、体重、胸囲、腹囲、足のサイズなどたくさんの体の特徴量があったとします。これらの特徴量はそれぞれ関係し合っているので、全部を使わずとも、いくつかの重要な特徴だけで体格の特徴をだいたい捉えることができるはずです。主成分分析を使うと、これらの特徴量の中から、体格を表すのに最も重要な指標(主成分)を見つけ出すことができます。そして、この少数の主成分を使うことで、データの解釈や処理を簡単にすることが可能になります。