過学習:未知への対応力を高めるには

AIを知りたい
先生、『過学習』って、学習データにぴったり合いすぎて、新しいデータへの対応が悪くなることですよね?具体的にどういうことか、もう少し分かりやすく教えてください。

AIエンジニア
そうだね。例えるなら、暗記に頼りすぎた受験勉強みたいなものだよ。過去問は完璧に解けるのに、初めて見る問題だと全く歯が立たない、そんな状態だ。

AIを知りたい
なるほど。じゃあ、たくさんの問題を解けばいいというわけではないんですね。暗記だけでなく、ちゃんと理解することが大事なんですね。

AIエンジニア
その通り!AIも同じで、与えられたデータの特徴だけでなく、本質を捉えるように学習させることが重要なんだ。そうすることで、未知のデータにも対応できるようになるんだよ。
過学習とは。
人工知能の分野でよく使われる「過学習」という言葉について説明します。「過学習」とは、別名「過剰適合」とも呼ばれる現象で、学習に使うデータだけにぴったり合うように学習し過ぎた結果、まだ知らないデータに対する予測能力が落ちてしまうことを指します。
過学習とは

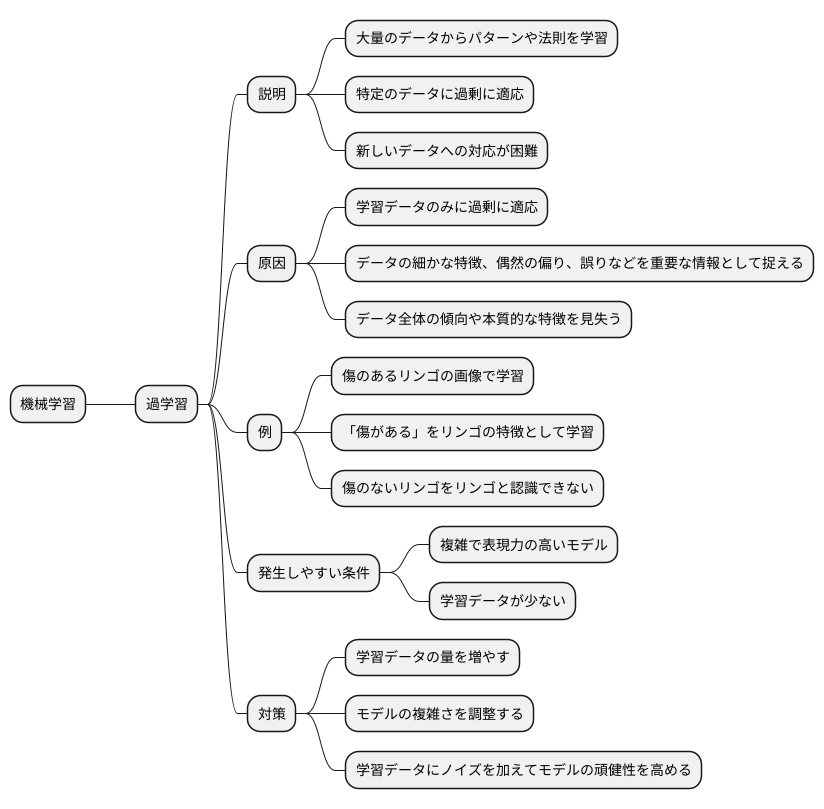
機械学習では、コンピュータに大量のデータを与えて、データの中に潜むパターンや法則を見つけ出させ、未知のデータに対しても予測や判断ができるように学習させます。しかし、学習方法によっては、まるで特定の問題集の解答だけを丸暗記した生徒のように、与えられたデータのみに過剰に適応してしまうことがあります。これが「過学習」と呼ばれる現象です。
過学習状態のコンピュータは、学習に用いたデータに対しては非常に高い精度で予測できますが、新しいデータに対してはうまく対応できません。これは、学習データに含まれる細かな特徴や、たまたま生じた偶然の偏り、あるいはデータに紛れ込んだ誤りまでも、重要な情報として捉えてしまうからです。本来捉えるべきデータ全体の傾向や本質的な特徴を見失い、学習データの表面的な部分に囚われてしまうのです。
例えるならば、果物の種類を判別する学習をさせるとします。学習データにたまたま傷のあるリンゴが多く含まれていた場合、過学習を起こしたコンピュータは、「傷がある」という特徴をリンゴを見分けるための重要な要素として学習してしまいます。その結果、傷のないリンゴを見せられても、リンゴだと判断できなくなる可能性があります。
この過学習は、複雑で表現力の高いモデルを用いた場合や、学習データの数が少ない場合に発生しやすくなります。複雑なモデルは、複雑なパターンを捉える能力が高い反面、細かなノイズにも敏感に反応してしまいます。学習データが少ない場合は、データ全体の傾向を十分に把握できず、一部のデータの特徴に引っ張られやすくなります。
過学習を防ぐためには、学習データの量を増やす、モデルの複雑さを調整する、学習データにノイズを加えてモデルの頑健性を高めるといった対策が有効です。適切な対策を施すことで、コンピュータが真に役立つ知識を獲得し、様々な状況に柔軟に対応できるようになります。
過学習の兆候

学習を深めすぎると、せっかく作った予測の仕組みが、新しいデータにうまく対応できなくなることがあります。これを過学習と呼びます。過学習は、まるで特定の問題を解くためだけに暗記した生徒のように、新しい問題に直面すると全く歯が立たなくなる状態です。この過学習が起こっているかどうかを見抜くためには、いくつかの手がかりがあります。
最もわかりやすい手がかりは、練習問題に対する成績は抜群なのに、本番の試験では全く点が取れないという状態です。これは、予測の仕組みを作るために使った練習用のデータ(訓練データ)に対しては、ほぼ完璧な予測ができるにもかかわらず、新しいデータ(検証データやテストデータ)に対しては、役に立たない予測しかできないことを意味します。まるで練習問題だけを暗記して、問題の解き方を理解していない生徒のようです。
また、予測の仕組みの中身が複雑になりすぎているというのも、過学習の手がかりです。これは、予測の仕組みを調整するツマミ(パラメータ)の値が非常に大きくなっている状態に例えられます。ツマミを細かく調整しすぎているため、練習問題には完璧に対応できるものの、少し違う問題が出されると対応できなくなってしまうのです。
学習の進み具合を示すグラフ(学習曲線)からも手がかりを得られます。練習問題に対する正答率は上がり続けるのに、本番の試験を想定した検証データに対する正答率が伸び悩み、やがて横ばいになる場合も、過学習が疑われます。これは、学習を続けるほど練習問題に特化しすぎてしまい、応用力がなくなっていることを示しています。
これらの手がかりが見つかった場合は、過学習への対策が必要です。対策をせずに学習を続けると、せっかくの予測の仕組みが使い物にならなくなってしまいます。過学習は、適切な対策を施すことで防ぐことができます。まるで生徒に暗記ではなく、問題の解き方を理解させるように、予測の仕組みも新しいデータに対応できるような、柔軟な仕組みを作る必要があるのです。
| 手がかり | 説明 | 例え |
|---|---|---|
| 訓練データに対する成績は良いが、検証/テストデータに対する成績が悪い | 訓練データに過剰に適合し、汎化能力が低い | 練習問題は完璧に解けるが、本番の試験では点が取れない生徒 |
| モデルが複雑になりすぎている | パラメータの値が非常に大きくなっている | ツマミを細かく調整しすぎて、少し違う問題に対応できない |
| 学習曲線において、訓練データの正答率は上昇し続けるが、検証データの正答率は伸び悩み、横ばいになる | 学習が進むにつれて、訓練データに特化しすぎて応用力がなくなる | 練習問題に特化しすぎて、応用力がなくなっている生徒 |
過学習を防ぐ対策

学習を効果的に進めるためには、学習した内容をしっかりと記憶するだけでなく、未知の状況にも対応できる能力、つまり汎化性能を向上させることが重要です。しかし、学習データに過度に適合しすぎてしまい、新しいデータに対する予測精度が低下してしまう現象、いわゆる過学習が発生することがあります。この過学習を防ぐためには、幾つかの対策があります。
まず、学習に用いるデータの量を増やすことが挙げられます。データが豊富にあれば、学習する対象の全体像を捉えやすくなり、特定のデータの特徴に偏ることなく、本質的な部分を学ぶことができます。例えるなら、様々な種類の木の写真をたくさん見ていれば、木の形や色の違いはあっても、共通して幹や枝、葉があることを理解し、「木」というものを正しく認識できるようになるでしょう。
次に、学習モデルの複雑さを調整することも大切です。複雑すぎるモデルは、学習データの細かな特徴にまで過剰に反応し、全体的な傾向を見失いがちです。これは、複雑な図形を覚える際に、細部まで完璧に記憶しようとするあまり、図形全体の形状を捉え損なうのと似ています。モデルを単純化することで、学習データの主要な特徴を捉え、本質的な部分を学習することができます。具体的には、モデルの層の数を減らす、あるいは各層の要素の数を減らすなどの調整を行います。また、正則化と呼ばれる手法を用いて、特定の特徴に過度に影響されないように調整することも有効です。
さらに、交差検証法を用いることも有効な手段です。これは、学習データを複数のグループに分け、それぞれのグループで学習と検証を繰り返す方法です。全てのグループで検証することで、学習モデルの汎化性能をより正確に評価し、過学習の兆候を早期に発見することができます。これは、テスト勉強で、教科書の章ごとに練習問題を解き、理解度を確認するようなものです。それぞれの章の問題を解くことで、全体の理解度を確かめることができます。
| 対策 | 説明 | 例え |
|---|---|---|
| 学習データの量を増やす | データが豊富だと全体像を捉えやすく、特定のデータの特徴に偏ることなく本質的な部分を学べる。 | 様々な種類の木の写真をたくさん見ることで「木」を正しく認識できるようになる。 |
| 学習モデルの複雑さを調整する | 複雑すぎるモデルは細かな特徴に過剰に反応し、全体的な傾向を見失う。モデルを単純化することで、主要な特徴を捉え、本質的な部分を学習できる。 | 複雑な図形を覚える際に、細部まで完璧に記憶しようとするあまり、図形全体の形状を捉え損なう。 |
| 交差検証法を用いる | 学習データを複数のグループに分け、それぞれのグループで学習と検証を繰り返すことで、汎化性能をより正確に評価し、過学習の兆候を早期に発見できる。 | テスト勉強で、教科書の章ごとに練習問題を解き、理解度を確認する。 |
正則化による抑制

正則化とは、機械学習モデルが学習データに過剰に適合してしまう、いわゆる過学習を防ぐための重要な手法です。過学習が発生すると、モデルは学習データには非常に高い精度を示しますが、未知のデータに対しては精度が低くなってしまいます。これは、モデルが学習データの細かなノイズや特殊なパターンまで学習してしまい、データの背後にある本質的な規則を捉えられていないことが原因です。
正則化は、モデルの複雑さを抑制することで、この過学習問題に対処します。具体的には、モデルのパラメータ(重み)にペナルティを科すことで、パラメータの値が大きくなりすぎるのを防ぎます。パラメータの値が大きいと、モデルは複雑になりやすく、過学習のリスクが高まります。正則化によってパラメータの値を小さく抑えることで、モデルをより単純化し、過学習しにくい状態に導きます。
代表的な正則化手法として、L1正則化とL2正則化が挙げられます。L1正則化は、パラメータの絶対値の和をペナルティ項として加えます。この方法の特徴は、重要でないパラメータをゼロにする効果があることです。つまり、モデルから不要な特徴量を自動的に選択する働きがあります。結果として、モデルが簡素化され、解釈しやすくなるという利点があります。
一方、L2正則化は、パラメータの二乗の和をペナルティ項として加えます。L2正則化は、すべてのパラメータを小さくする方向に働きかけます。厳密にゼロになるパラメータは少ないですが、パラメータ全体の大きさを抑制することで、モデルの出力の変化を滑らかにします。これにより、学習データのノイズの影響を受けにくくなり、安定した予測が可能になります。
L1正則化とL2正則化は、それぞれ異なる特性を持つため、問題に応じて適切な方法を選択することが重要です。どちらの方法も、過学習を抑制し、未知のデータに対しても高い予測精度を実現する上で重要な役割を果たします。つまり、モデルの汎化性能を高めるために有効な手段と言えるでしょう。
| 正則化手法 | ペナルティ項 | 効果 | 利点 |
|---|---|---|---|
| L1正則化 | パラメータの絶対値の和 | 重要でないパラメータをゼロにする | モデルの簡素化、解釈性の向上 |
| L2正則化 | パラメータの二乗の和 | すべてのパラメータを小さくする | ノイズの影響を受けにくい、安定した予測 |
データ拡張の活用

データの拡張は、少ない手持ちの学習情報を増やすための技術です。
まるで種から多くの芽を出すように、元となるデータをもとに人工的に様々な形の新しいデータをたくさん作り出します。これにより、実際に集めたデータ量以上の学習効果が期待できます。
例えば、写真を見て何が写っているかを機械に学習させる場面を考えてみましょう。学習に使える写真が少ない場合、機械は限られた情報しか覚えられず、学習がうまくいかないことがあります。
このような場合にデータ拡張が役立ちます。一枚の写真を色々な角度に回転させたり、左右反転させたり、明るさを変えたりすることで、元の写真一枚から複数枚の新しい写真を作れます。
これらは全て同じ被写体ですが、機械にとっては別の新しい写真に見えます。こうしてデータの数を増やすことで、機械はより多くのパターンを学習し、写真の識別精度を向上させることができます。
音声の認識に関しても同じ考え方でデータ拡張ができます。例えば、ある人の声を機械に学習させたい場合、録音データが少ないと、機械はその人の声をうまく聞き分けられない可能性があります。そこで、録音データに少し雑音を加えたり、声の高低を少し変えたりすることで、様々なバリエーションの音声データを作成します。
機械はこれらの変化した音声も学習することで、元の音声と似た音声をより正確に聞き分けられるようになります。
このように、データ拡張は、学習データが少ない状況でも、機械学習の効果を高める上で非常に役立つ技術です。特に、データを集めるのが難しい場合やコストがかかる場合に有効な手段となります。データ拡張によって、過学習と呼ばれる、機械が学習データに過剰に適応してしまい、新しいデータに対応できなくなる現象を防ぐ効果も期待できます。
データ拡張は、限られた資源から最大限の学習効果を引き出すための、とても大切な技術と言えるでしょう。
| 種類 | 拡張方法 | 効果 |
|---|---|---|
| 画像 | 回転、反転、明るさ変更 | 識別精度向上 |
| 音声 | 雑音追加、高低変更 | 認識精度向上 |
適切なモデル選択

機械学習では、目的とする課題をうまく解決するために、数多くの手法の中から適切なモデルを選ぶことが大切です。モデルとは、データの背後にある規則性やパターンを表現するための数式のようなものです。まるで職人が道具を選ぶように、データ分析を行う人も、データの特徴や課題の性質に合わせて最適なモデルを選ばなければなりません。
モデル選びで重要なポイントの一つに、モデルの複雑さがあります。複雑なモデルは、データの細かい変化まで捉えることができます。これは、複雑な模様を描くことのできる多機能な絵筆のようなものです。しかし、あまりに複雑すぎると、学習データの些細な特徴にまで過剰に適応してしまい、新しいデータに対する予測精度が落ちてしまうことがあります。これは、絵筆の使い方を練習しすぎて、お手本の絵は完璧に再現できるようになったものの、自由に絵を描くことができなくなってしまうようなものです。このような状態を過学習と呼びます。
一方で、単純なモデルは、データのおおまかな傾向しか捉えることができません。これは、一本の線しか引くことのできないシンプルな鉛筆のようなものです。しかし、単純なモデルは過学習しにくいという利点があります。新しいデータに対しても、比較的安定した予測ができます。
では、どのように適切な複雑さのモデルを選べば良いのでしょうか?一つの方法は、データの量に着目することです。データが豊富にある場合は、複雑なモデルを使っても過学習のリスクは低くなります。多くの練習問題を解いたおかげで、試験でも様々な問題に対応できるようになるようなものです。逆に、データが少ない場合は、単純なモデルを選ぶ方が賢明です。限られた情報から全体像を推測するには、単純な考え方の方が有効な場合があります。
また、複数のモデルを組み合わせて使うという方法もあります。これは、鉛筆と絵筆、ペンなど、複数の道具を組み合わせて絵を描くようなものです。それぞれのモデルの得意な部分を活かすことで、単一のモデルを使うよりも高い予測精度を達成できる場合があります。
適切なモデルを選ぶことは、機械学習の成功に欠かせない要素です。データの特性や課題の性質をじっくりと見極め、最適なモデルを選び、予測精度を高めていきましょう。
| モデルの複雑さ | 特徴 | メリット | デメリット | データ量 | 例え |
|---|---|---|---|---|---|
| 複雑 | データの細かい変化まで捉える | 複雑なパターンを表現可能 | 過学習しやすい | 多量 | 多機能な絵筆 |
| 単純 | データのおおまかな傾向を捉える | 過学習しにくい、安定した予測 | 細かい変化に対応できない | 少量 | シンプルな鉛筆 |
| 複数モデルの組み合わせ | それぞれのモデルの得意な部分を活かす | 単一モデルより高精度な予測 | – | – | 鉛筆、絵筆、ペンなど複数の道具 |
